Лачин Электроника. Электроника рекомендовано Министерством образования Российской Федерации в качестве учебного пособия ля студентов высших технических учебных заведений РостовнаДону Феникс 2001 Рецензенты
 Скачать 7.57 Mb. Скачать 7.57 Mb.
|
|
4.1. ВВОДНЫЕ СВЕДЕНИЯ ПО МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ ЭЛЕКТРОННЫХ УСТРОЙСТВ Математическое моделирование — это использование вместо реального объекта его математической модели. В свою очередь математическая модель по существу является количественным описанием объекта. Слово «математическая» в термине «математическая модель» подчеркивает тот факт, что это описание отличается строгим математическим характером. Для современного специалиста исключительно важно осознать следующий факт. К настоящему времени развитие науки достигло такого уровня и количественное описание различных объектов является настолько точным, что очень многая отсутствующая информация об объекте может быть получена на основе только этого описания, без использования самого объекта. В определенном смысле математическое моделирование — это уровень развития науки в настоящее время. Особую роль при математическом моделировании играет ЭВМ, являющаяся инструментом моделирования. Математическое моделирование радикально повышает эффективность труда специалиста. Особенно важную роль математическое моделирование играет в электронике. Здесь наиболее существенными являются следующие обстоятельства: • большая сложность и большое разнообразие электронных устройств; традиционные методы анализа и синтеза и тем более интуитивные представления о работе устройств часто оказываются бесполезными;
Математическое моделирование электронной схемы начинается с ввода в ЭВМ информации об электронных приборах (или элементах и компонентах интегральных схем) и способе их соединения. При использовании современных систем схемотехнического моделирования, оснащенных специальными программами (так называемыми графическими редакторами), ввод указанной информации обеспечивается изображением на экране ЭВМ электрической принципиальной схемы моделируемого устройства и указанием типов электронных приборов. На рис. 4.1 приведен пример электронной схемы (RC-усилителя на биполярном транзисторе), подготовленной 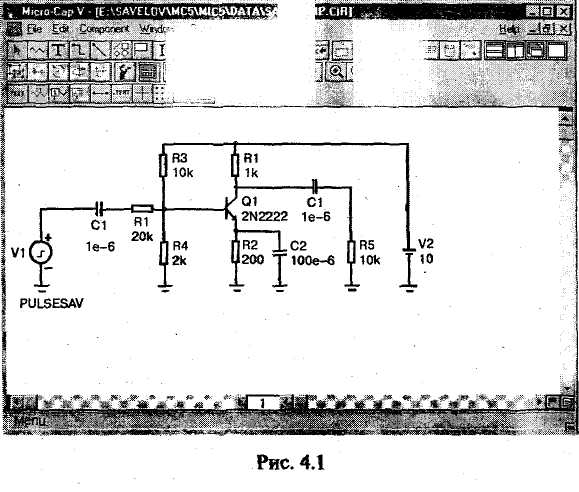 к моделированию с помощью пакета программ Micro-Cap-V. По указанному типу прибора система моделирования обращается к соответствующей математической модели прибора и заменяет ей прибор, изображенный на схеме. Как уже отмечалось при рассмотрении отдельных приборов, математическая модель прибора — это совокупность его эквивалентной схемы и математических выражений, описывающих элементы эквивалентной схемы. После замены каждого прибора его эквивалентной .схемой образуется математическая модель всего электронного устройства, т. е. совокупность эквивалентной схемы устройства и математических выражений, описывающих элементы этой эквивалентной схемы. Достаточные для первого ознакомления представления об использующихся математических моделях приборов дают рассмотренные выше модели диодов и транзисторов. 4.2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ РАЗЛИЧНЫХ РЕЖИМОВ РАБОТЫ ЭЛЕКТРОННЫХ устройств Современные программные системы (Micro-CapV, Design Center 6.2 и др.) позволяют автоматизированно моделировать практически все режимы работы электронного устройства, представляющие интерес для специалиста. Рассмотрим особенности моделирования различных режимов, используя их наименования, характерные для математического моделирования. Режим постоянного тока. Это режим покоя, начальный режим работы электронной схемы. При моделировании этого режима предполагается, что к электронному устройству уже достаточно долго подключены только источники постоянного напряжения и тока. Моделирование рассматриваемого режима основано на использовании метода Ньютона (Ньютона—Рафсона) для решения систем нелинейных уравнений или модификаций данного метода. Этот метод является итерационным. Характерной его особенностью является линеаризация системы нелинейных уравнений на каждом этапе вычисления очередной итерации (приближения к решению). Важно отметить, что в системах схемотехнического моделирования этот метод реализован не в классической форме, рассматриваемой в различных руководствах по вычислительным методам, а в оригинальной схемотехнической форме, отличающейся логической красотой, совершенством и ориентированной именно на моделирование электронных схем. Моделирующая программа, фактически решая систему нелинейных уравнений, описывающую электронное устройство, не формирует эту систему. Вместо этого при вычислении очередной итерации каждый нелинейный элемент эквивалентной схемы электронного устройства заменяется линейной так называемой дискретной моделью, соответствующей методу Ньютона. В результате образуется линейная схема, анализ которой и приводит к определению очередной итерации. Для полученной линейной схемы моделирующая программа формирует систему линейных узловых уравнений, в которой неизвестными являются узловые напряжения (потенциалы). Затем эта программа решает полученную систему линейных алгебраических уравнений, используя LU-факторизацию. LU-факторизация выполняется на основе метода исключения Гаусса для решения системы линейных алгебраических уравнений или по алгоритму Кра-ута, который по существу является модификацией метода исключения Гаусса. Современные моделирующие программы учитывают разреженность матрицы системы узловых уравнений. Это значительно сокращает затраты машинного времени и памяти. По завершении решения системы узловых уравнений определяются все остальные искомые токи* и напряжения схемы. После вычисления некоторого количества итераций (например, нескольких десятков) определяется решение, т. е. находится установившийся режим схемы. На рис. 4.2 приведен график зависимости напряжения VCE(Ql) между коллектором и эмиттером транзистора от напряжения питания V(V2) для схемы рис. 4.1. Этот график получен при анализе режима постоянного тока в результате многократного расчета установившегося режима. На рис. 4.3 показано соответствующее окно для задания параметров моделирования. Динамический режим. Этим термином обозначают режим работы электронного устройства, при котором могут иметь место различные переходные процессы. По существу динамический режим — это реальный режим работы 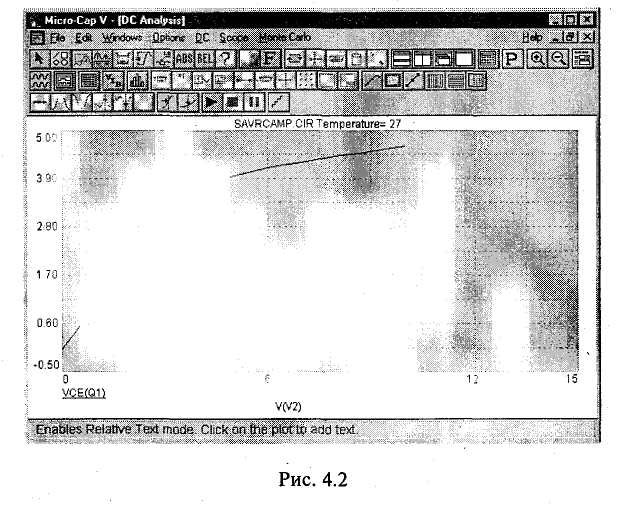  электронной схемы во всем его многообразии, развивающийся во времени. При моделировании динамического режима учитывается воздействие на схему самых разнообразных источников сигналов. Моделирование динамического режима основано на использовании неявных методов решения систем обыкновенных дифференциальных уравнений. Обычно используются методы Гира (формулы дифференцирования назад). В системах схемотехнического моделирования указанные методы также реализованы не в классической, а в специфической схемотехнической форме, в наивысшей степени соответствующей задаче моделирования переходных процессов в электронных схемах. Система моделирования вьшолняет численный расчет переходных процессов без формирования соответствующей системы обыкновенных дифференциальных уравнений. Для определения токов и напряжений схемы в некоторый следующей момент времени все реактивные элементы (конденсаторы и катушки индуктивности) заменяются дискретными моделями, соответствующими используемому неявному методу. В результате образуется схема без реактивных элементов, анализ которой и приводит к определению указанных токов и напряжений. Многократное повторение описанных действий и обеспечивает анализ динамического режима в течение достаточно длительного отрезка времени. На рис. 4.4 приведены временные диаграммы напряжений на входе (V(7)) и выходе (V(5)) схемы, полученные при анализе динамического режима. На рис. 4.5 показано соответствующее окно для задания параметров моделирования. Режим переменного тока. Это установившийся режим работы схемы при воздействии на нее синусоидального входного сигнала настолько малой амплитуды, что нели-  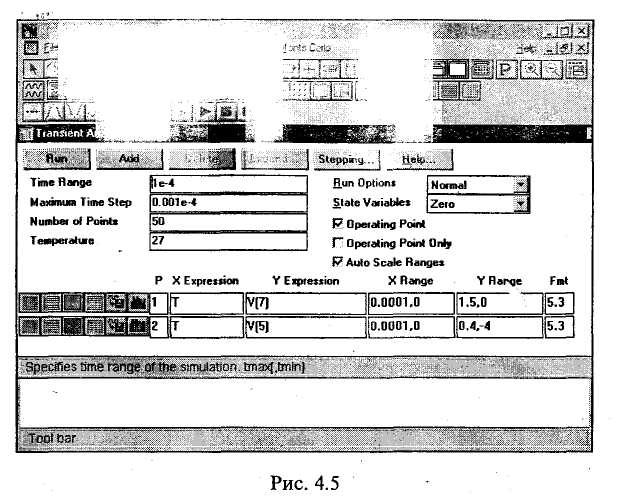 нейности характеристик электронных приборов не проявляются и схема может анализироваться как линейная. В рассматриваемом режиме определяют различные частотные характеристики электронных схем, наиболее употребительными из которых являются амплитудно-частотная и фазочастотная характеристики. Моделирование режима переменного тока основано на использовании комплексного (символического) метода анализа электронных схем. При этом для каждой частоты входного сигнала формируется система линейных алгебраических уравнений, описывающая рассматриваемый режим и имеющая комплексную матрицу коэффициентов и комплексный столбец правых частей. Решение этой системы позволяет определить переменные составляющие токов и напряжений и значения соответствующих параметров схемы. При этом используют те же указанные выше методы решения систем линейных алгебраических уравнений, которые применяются при анализе режима постоянного тока (для которого характерно применение вещественных матриц коэффициентов и столбцов правых частей). Повторение таких вычислений при различных частотах обеспечивает анализ рассматриваемого режима в требуемом диапазоне частот. На рис. 4.6 приведены амплитудно-частотная и фазо-частотная характеристики схемы рис. 4.1, полученные при анализе режима переменного тока. На рис. 4.7 показано соответствующее окно для задания параметров моделирования. 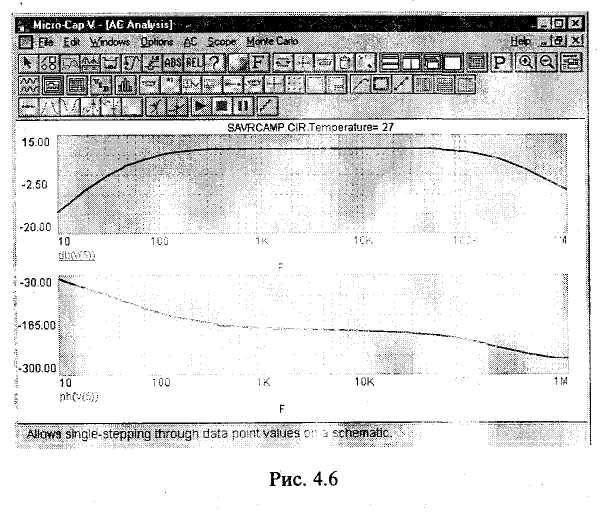 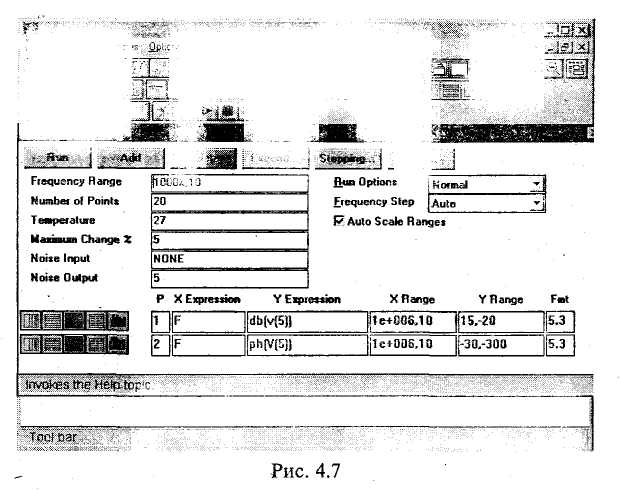 4.3. УРОВЕНЬ СОВРЕМЕННЫХ СИСТЕМ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРОННЫХ УСТРОЙСТВ Системы математического моделирования устройств электроники на протяжении длительного времени постоянно развиваются и совершенствуются. Укажем характерные возможности современных систем моделирования. Моделирование смешанных аналого-цифровых устройств. Электронная схема, подлежащая моделированию, может состоять как из аналоговых, так и цифровых устройств. Важно отметить, что допускается использование обратных связей. Цифровые устройства моделируются на логическом уровне. Система моделирования в автоматическом режиме обеспечивает взаимодействие аналоговых и цифровых устройств, поэтому математическая модель всего аналого-цифрового устройства электроники функционирует как единое целое, адекватно отражая особенности работы реального устройства. На рис. 4.8 приведен пример аналого-цифровой схемы, подготовленной к моделированию с помощью пакета Micro-Cap V. В этой схеме кроме аналоговых элементов используется JK-триггер. Статистический анализ. Для оценки влияния изменения параметров элементов электронной схемы (в рамках их заданных допусков) на режим ее работы, определение чувствительности режима работы схемы к изменению параметров элементов система моделирования выполняет многократный анализ схемы, случайным образом изменяя требуемые параметры элементов. При этом изменения выполняются в соответствии с конкретными законами распределения. Спектральный анализ. Сигналы, полученные при моделировании, можно подвергнуть спектральному анализу, разлагая в усеченный ряд Фурье. Могут учитываться более сотни гармоник. Анализ шумов. При моделировании предусмотрено задание шумовых параметров элементов электронных схем. 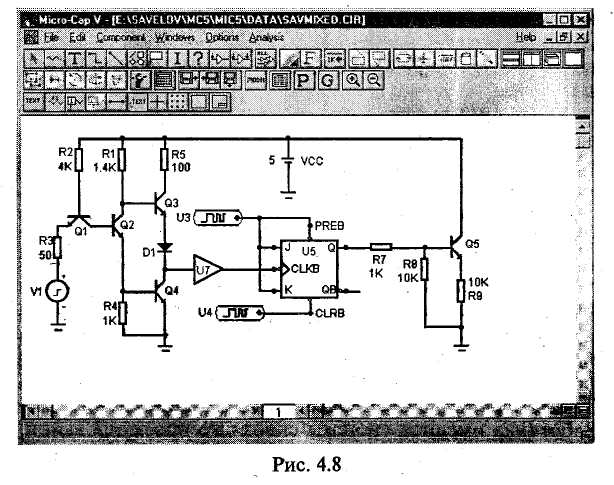 Использование этих параметров дает возможность оценивать шумовые свойства электронных устройств. Использование функциональных блоков. Отдельные узлы электронного устройства могут моделироваться как функциональные блоки, описываемые передаточными функциями. Нелинейные передаточные функции могут задаваться как аналитически, так и в табличной форме. Параметрический синтез (параметрическая оптимизация). Для конкретной схемы электронного устройства программная система может осуществить поиск наилучшего соотношения параметров элементов схемы в соответствии с заданной целевой функцией. Параметрический синтез позволяет создавать устройства электроники, обладающие наивысшими технико-экономическими показателями. Структурный синтез. Схемы электронных устройств отдельных классов (в частности, активных фильтров) могут создаваться в автоматизированном режиме в соответствии с заданными требованиями. Создание математических моделей элементов. Системы моделирования комплектуются программами, обеспечивающими получение в автоматизированном режиме математических моделей элементов электронных схем. При этом используются справочные данные, характеризующие эти элементы. На рис. 4.9 приведен пример графика зависимости коэффициента b транзистора от тока коллектора, который строится по точкам, задаваемым пользователем на основе справочных данных. Проектирование печатных плат. В последнее время появились программные системы (Design Center 6.2, Design Lab 8.0), обеспечивающие, кроме моделирования электромагнитных процессов, также и проектирование печатных плат электронных устройств. Ранее для этого проектирования использовались специализированные программы разработки печатных плат (P-CAD, OrCAD), которые не осуществляли моделирования этих процессов. Таким образом, в настоящее время в распоряжении разработчика имеются системы сквозного проектирования, обеспечивающие выполнение всех основных этапов разработки устройств электроники. 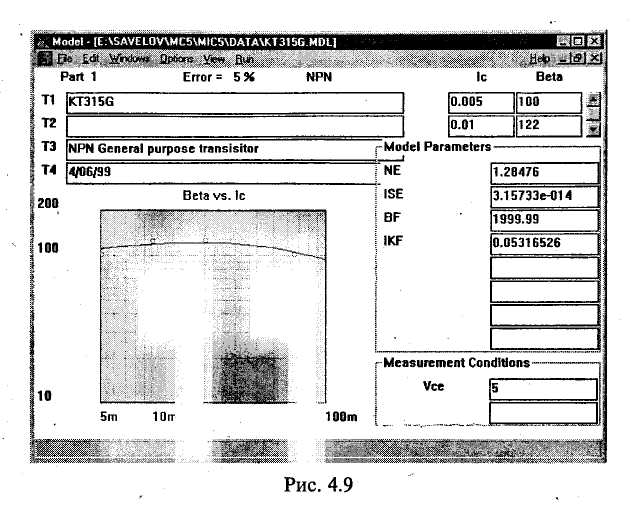 4.4. ВЛИЯНИЕ РАЗВИТИЯ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ НА ХАРАКТЕР ТРУДА РАЗРАБОТЧИКА ЭЛЕКТРОННЫХ УСТРОЙСТВ Для продуктивной работы по созданию устройств электроники важно осознать, что достижения математического моделирования электронных схем в очень сильной степени изменили характер работы современного специалиста. Теперь эффективность его деятельности непосредственно зависит от уровня подготовки в области моделирования. Уже можно утверждать, что без овладения основами математического моделирования практически нельзя надеяться на получение результатов, составляющих конкуренцию результатам работы тех специалистов, которые хорошо освоили моделирование. В то же время важно рассмотреть вопрос о том, что может дать математическое моделирование и чего оно, по крайней мере в настоящее время, дать не может. Математическое моделирование берет на себя многие прежние обязанности разработчика электронных схем, но при этом возлагает на него новые обязанности, что можно считать вполне справедливой платой за новые, исключительно полезные возможности. Существует заблуждение, в соответствии с которым использование математического моделирования освобождает от необходимости глубоко изучать особенности построения конкретных электронных схем, а также происходящих в них процессов. Возможно, это заблуждение возникло потому, что математическое моделирование в высшей степени полезно для уяснения самых сложных вопросов, возникающих при изучении электронных схем, и поэтому во многих случаях быстро компенсирует пробелы в начальной подготовке. Но это не оправдывает заблуждение, а говорит только о том, что математическое моделирование следует использовать все более широко и на все более ранних этапах изучения электроники. Что же касается самих знаний в области электроники, то они безусловно необходимы для плодотворной работы с использованием пакетов схемотехнического моделирования. Современный этап математического моделирования характерен тем, что практически все ключевые решения при создании электронной схемы принимает разработчик, а не система моделирования. Поэтому недопонимание тех или иных особенностей электронной схемы приводит к выбору неоптимальных вариантов схемы, значений параметров элементов, а также режимов работы. При этом существует опасность, что моделирование не выявит все характерные режимы работы схемы, в том числе и опасные, так как именно разработчик определяет начальные условия моделирования. Нужно осознать, что основная функция моделирующей программы состоит в получении численных значений тех или иных переменных, определяемых по достаточно жестким алгоритмам. Моделирование не снимает с разработчика обязанности качественной интеллектуальной оценки и самой схемы, и происходящих в ней процессов. На разработчике лежит вся ответственность за окончательный выбор конкретной схемы даже в случае автоматизированного структурного синтеза типовых устройств. Он должен или непосредственно устанавливать, или изменять параметры элементов схемы, или определять целевую функцию для параметрического синтеза. Успешно решать эти задачи можно только при глубоком понимании работы устройства. Необходимым является знание основных количественных соотношений, характеризующих электронную схему и являющихся основой для выбора начальных значений параметров элементов, а также направления и степени изменения этих параметров. Приступая к математическому моделированию, следует уяснить, что необходимым условием для получения положительных результатов являются знания в области математических моделей элементов и методов вычислений, реализованных в моделирующих программах. Важно с самого начала понять, что результаты моделирования некоторой электронной схемы определяются не только ее характерными особенностями, но и особенностями используемых математических моделей и алгоритмов. Здесь будет кстати вспомнить тот факт, что и при экспериментальном исследовании реальных электронных устройств результаты зависят и от особенностей организации эксперимента, и от параметров измерительных приборов. Точно так же, как неправильная настройка экспериментальной установки и использование не соответствующих цели эксперимента испытуемых образцов и приборов являются причинами ошибочных экспериментальных результатов, неправильные применение математических моделей, настройка и использование вычислительных алгоритмов приводят к получению ошибочных результатов моделирования. Конечно, некоторые пользователи предпочли бы те программные средства, которые вообще не требуют знания использующихся в них моделей и методов моделирования. Однако таких программных средств не существует и они вряд ли появятся. Характерной чертой прежних подходов к анализу и проектированию электронных схем является то, что для каждого отдельного класса электронных схем (усилители, стабилизаторы и т. д.) используются специализированные приемы и методы. Эти приемы и методы, как правило, логически слабо связаны. Поэтому слабо связаны и различные разделы руководств по расчету электронных схем. Современные подходы к математическому моделированию электронных схем характерны использованием достаточно малого числа универсальных эффективных методов, основанных на последних достижениях прикладной математики и электроники. Эти методы позволяют выполнять анализ и расчет различных электронных схем единообразно, с использованием единых исходных позиций. Но данные методы, отличающиеся глубиной реализуемых идей, достаточно сложны. Их усвоение требует глубокой всесторонней проработки. Представляется возможным провести аналогию между переходом к современным методам моделирования и переходом к широкому использованию дифференциального исчисления, сделавшим ненужными многие прежние приемы и способы решения конкретных частных задач математики. Однако дополнительные обязанности разработчика электронных схем по выбору, созданию и корректировке математических моделей, настройке моделирующих программ и контролю за их работой многократно компенсируются возможностями быстро и с высокой точностью выполнять самые сложные расчеты, абсолютно невозможные при использовании прежних подходов. Математическое моделирование освобождает от рутинной работы и радикально увеличивает возможности для творчества в электронике. ЛИТЕРАТУРА
- 768 с.
- 371 с. ТЗ. - М.: Мир, 1993. - 367 с. 10. Прянишников В.А. Электроника: Курс лекций. — СПб.: Корона-принт, 1998. — 400 с. Учебное пособие В. И. Лачин, Н. С. Савёлов ЭЛЕКТРОНИКА Ответственный редактор И. Жиляков Обложка Т. Неклюдова Корректоры: В. Югобашьян, Н. Передистый Лицензия ЛР № 065194 от 2 июня 1997 г. Сдано в набор 15.07.01. Подписано в печать 25.08.01. Формат 84x108/32. Бумага тип. № 2 Гарнитура NewtonC. Печать высокая. Усл. печ. л. 23,52. Тираж 5000 экз. Заказ №43. Налоговая льгота — общероссийский классификатор продукции ОК-00-93, том 2; 953000 — книги, брошюры Издательство «Феникс» 344007, г. Ростов-на-Дону, пер. Соборный, 17. Отпечатано с готовых диапозитивов в ЗАО «Книга» 344019, г. Ростов-на-Дону, ул. Советская, 57. |
