Элементами. Из определения следует, что элементы множества обладают двумя свойствами 1 вполне различимы 2
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
частью графа G(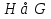 ), если мн-во V(H) и мн-во ребер E(H) содержится в соответствующих мн-вах для графа G: ), если мн-во V(H) и мн-во ребер E(H) содержится в соответствующих мн-вах для графа G:  и и 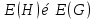 . .Граф H называется суграфом графа G, если он является частью графа G и кол-во вершин графа H равно кол-ву вершин графа G, т.е.V(H)=V(G). Граф G( 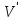 ) назыв. подграфом графа G(V), если граф G( ) назыв. подграфом графа G(V), если граф G(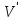 ) содержит все ребра, которые инцидентны вершинам из мн-ва ) содержит все ребра, которые инцидентны вершинам из мн-ва 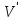 . .Определим некоторые операции на графах:
Дополнение 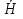 части H графа G явл. графом удовлетворяющим след. условиям: части H графа G явл. графом удовлетворяющим след. условиям:1) 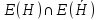 = = 2) 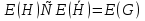 Операции: Сумма 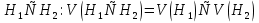 и и 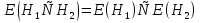 Произведение 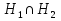 : : 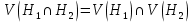 и и 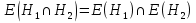 43. Ориентированные и неориентированные графы. Графом G называется совокупность 2-х множеств (V, E), где V – множество вершин графа, а Е – множество ребер графа. Между вершинами и ребрами графа G устанавливают отношение инцидентности. Считают, что ребро 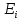 инцидентно вершинам инцидентно вершинам 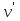 , , 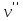 , если оно соединяет эти 2-е вершины. При этом вершины , если оно соединяет эти 2-е вершины. При этом вершины 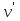 , , 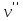 называются смежными. Отношение инцидентности является самым главным элементом графа, т.к. указывает способ объединения множеств V и E в единый объект. Если ребро называются смежными. Отношение инцидентности является самым главным элементом графа, т.к. указывает способ объединения множеств V и E в единый объект. Если ребро 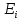 , соединяющее 2-е вершины, направлено от одной вершины к другой, то оно называется ориентированным или дугой и графически изображается стрелками, направленными от начала к концу. Граф, содержащий дуги называется ориентированным или орграфом. Граф, не содержащий ни одной дуги (содержащий только ребра) называется неориентированным или н-графом. , соединяющее 2-е вершины, направлено от одной вершины к другой, то оно называется ориентированным или дугой и графически изображается стрелками, направленными от начала к концу. Граф, содержащий дуги называется ориентированным или орграфом. Граф, не содержащий ни одной дуги (содержащий только ребра) называется неориентированным или н-графом. Пример. 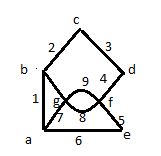 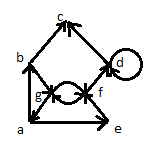 Н-ГРАФ (Рис.1) ОР-ГРАФ(Рис.2) Ребра, инцидентные одной и той же паре вершин называются кратными (на рис.1 это ребра 8 и 9). 44.Маршруты. Пути. Цепи. Связные графы. Пусть G – н-граф. Маршрутом М графа G называется такая последовательность ребер ( 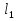 , , , … , , … , 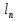 ), в которой два ребра ), в которой два ребра 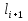 , , 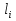 имеют общую вершину. В маршруте одно и то же ребро может встречаться несколько раз. Начало маршрута имеют общую вершину. В маршруте одно и то же ребро может встречаться несколько раз. Начало маршрута 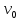 . . 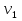 инцидентно инцидентно 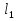 . . 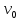 не инцидентно не инцидентно  . .Маршрут, начало и конец которого совпадают называется циклическим. Маршрут, в котором все ребра разные – цепь. Цепь, не имеющая повторяющихся вершин, называется простой цепью. Циклический маршрут, являющийся цепью, называется циклом, являющийся простой цепью – простым циклом. Вершины 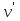 , , 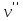 называются связанными, если существует маршрут М с началом в называются связанными, если существует маршрут М с началом в 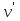 и концом в и концом в 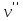 . .Связанные маршрутом вершины, связаны также и простой цепью. Причем отношение связности обладает свойством эквивалентности и определяет разбиение множества V(G) на не пересекаемые множества V:(G) связных вершин. Граф G называется связным, если все его вершины связаны между собой. Если граф G несвязный, то связными будут множества V:(G), которые называются связными компонентами графа. Каждый н-граф распадается единственным образом на прямую сумму своих связных компонентов. Пример.  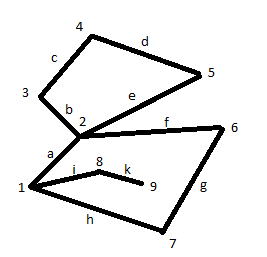 Пусть G – орграф. Последовательность дуг, в которой конец предыдущей дуги  совпадает с началом следующей дуги, называется путем. Одна и та же дуга в пути может встречаться несколько раз. Путь называется ориентированной цепью, если каждая дуга встречается не больше одного раза; простой цепью – если не содержит повтор вершин. Замкнутый путь называется контуром. Контур называется циклом, если путь является цепью; простым циклом – если простой цепью. Граф называется связным, если он связан без учета ориентации дуг, и сильно связным, если из любой вершины графа в любую другую существует путь. Число дуг пути называется его длиной. совпадает с началом следующей дуги, называется путем. Одна и та же дуга в пути может встречаться несколько раз. Путь называется ориентированной цепью, если каждая дуга встречается не больше одного раза; простой цепью – если не содержит повтор вершин. Замкнутый путь называется контуром. Контур называется циклом, если путь является цепью; простым циклом – если простой цепью. Граф называется связным, если он связан без учета ориентации дуг, и сильно связным, если из любой вершины графа в любую другую существует путь. Число дуг пути называется его длиной. Определение. Путь называется простым, если все вершины графа, по которым он проходит, различны (более одного раза не проходит по одной вершине). Определение. Путь называется замкнутым, если он начинается и заканчивается в одной и той же вершине (v0 = vn). Определение. Циклом называется замкнутый путь, не проходящий более одного раза по одному и тому же ребру. Определение. Цикл называется простым, если он более одного раза не проходит через одну и ту же вершину, то есть v0, …, vn-1 – различные. 45. Геометрическая реализации графа. Теорема о реализации конечного графа в трёхмерном пространстве. Определение. Пусть задан некоторый неориентированный граф G = (V, E). Пусть любой вершине vi графа G сопоставлена некоторая точка ai: vi→ ai, ai≠ aj(i ≠ j), а любому ребру e = (a, b) сопоставлена некоторая непрерывная кривая L, соединяющая точки aiи ajи не проходящая через другие точки ak(k ≠ i, j). Тогда если все кривые, сопоставленные рёбрам, не имеют общих точек, кроме концевых, то говорят, что задана геометрическая реализация графа G.  Теорема. Для любого графа существует его реализация в трёхмерном пространстве. Доказательство. Возьмём в пространстве любую прямую l и разместим на ней все вершины графа G. Пусть в G имеется q рёбер. Проведём связку из q различных полуплоскостей через l. После этого каждое ребро графа G можно изобразить линией в своей полуплоскости и они, очевидно, не будут пересекаться. Теорема доказана. 46.Эйлеровы циклы. Задача о кенигсбергских мостах. Теорема Эйлера. Опр. Цикл, содержащий все ребра графа, называется эйлеровым циклом. Опр. Граф, содержащий эйлеровы циклы, называется эйлеровым графом. 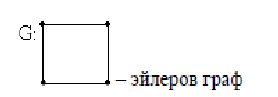 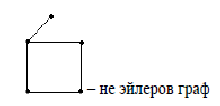 Опр. Эйлеров граф – граф, который можно изобразить одним росчерком пера, причем процесс такого изображения должен начинаться и заканчиваться в одной и той же точке.  Теорема Эйлера. Конечный неориентированный граф 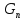 эйлеров тогда и только тогда, когда он связен и степени всех его вершин четные. эйлеров тогда и только тогда, когда он связен и степени всех его вершин четные.Задача о кенигсбергских мостах. Можно ли пройти по всем мостам, не проходя дважды ни по одному из них(можно ли на этом графе построить цикл, не содержащий повторяющихся ребер, который проходит через все ребра графа)? В ходе рассуждений Эйлер пришёл к следующим выводам:
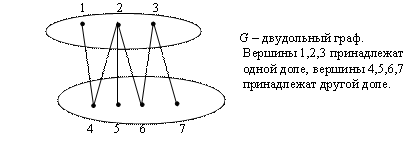
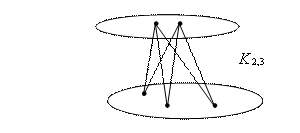
Граф кёнигсбергских мостов имел четыре нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды. 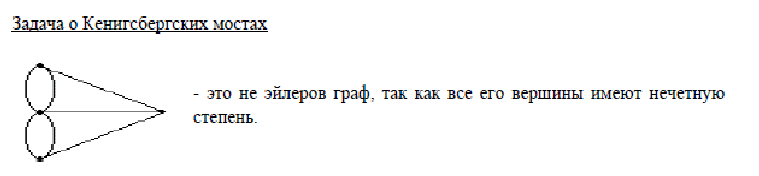 47.Обобщенная теорема об эйлеровых цепях. Эйлерова цепь – цепь н-графа, содержащая все его ребра, имеющая различные начальные и конечные точки. Теорема. Если граф G связен и имеет 2k вершин нечетной степени, то в нем можно выделить ровно k цепей, содержащих в совокупности все ребра графа ровно по одному разу. Обозначим буквами 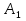 , , 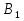 , , 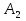 , , 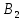 , … , , … , 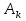 , , 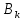 вершины , имеющие нечетные степени и соединим ребрами вершины: вершины , имеющие нечетные степени и соединим ребрами вершины: 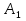 , , 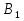 – – 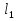 , … , , … , 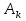 , , 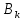 – – 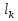 , т.е. добавим к графу G еще k ребер. , т.е. добавим к графу G еще k ребер.В новом графе степени всех вершин четны, следовательно, существует эйлеров цикл. Если из найденного эйлерова цикла удалить новые ребра, то он распадется на k отдельных частей, содержащих все ребра исходного графа. Пример. 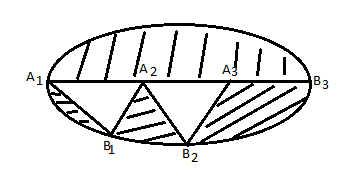 На рисунке изображена схема трамвайных путей. Требуется выбрать маршруты движения так, чтобы можно было добраться до любой точки схемы, делая пересадки только в вершинах графа. 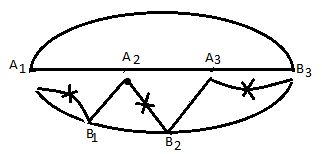 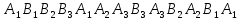 Граф распадается на 3-и цепи. 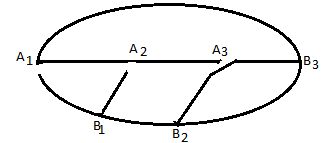 Теорема. Чтобы в конечном ориентированном графе G существовал эйлеров цикл, необходимо и достаточно равенство степеней всех вершин этого графа по входящим и выходящим дугам 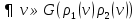 .Учитывая, что любому н-графу канонически соответствует орграф, можно сформулировать следующее утверждение: в конечном связном н–графе всегда можно построить ориентированный цикл, проходящий через каждую дугу (проходящий через каждое ребро по одному разу в каждом из двух направлений). .Учитывая, что любому н-графу канонически соответствует орграф, можно сформулировать следующее утверждение: в конечном связном н–графе всегда можно построить ориентированный цикл, проходящий через каждую дугу (проходящий через каждое ребро по одному разу в каждом из двух направлений).48. Гамильтоновы графы. Задача о коммивояжере. Определение. Гамильтоновым циклом называется простой цикл, проходящий через все вершины рассматриваемого графа. Если данный маршрут не замкнут, он называется гамильтоновой цепью. Заметим, что проблема существования гамильтонова пути принадлежит к классу так называемых NP-полных задач. Известно лишь достаточное условие существования гамильтоновой цепи на графе. Оно звучит следующим образом: если степень каждой вершины графа, который имеет n вершин (n>= 3) , не меньше n / 2, то на этом графе можно построить гамильтонову цепь. Практическим применением гамильтоновых графов является «задача коммивояжера», которая формулируется следующим образом. Коммивояжеру требуется выбрать кратчайший маршрут, посетив только по одному разу каждый из заданных пунктов, расстояния между которыми известны, и возвратиться в исходный пункт. A B C D 7 6 8 4 1 5 Рис.7. Рис.6. Задачу коммивояжера можно решить методом перебора: составить все возможные маршруты, найти их длину и выбрать кратчайший маршрут. Например: на рис. 7 представлена схема маршрутов, известны расстояния между городами АВ=7, АС=5, АД=4, ВС=6, ВД=1, СД=8 Всего возможных циклов шесть –АВСДА, АСВДА, АВДСА, АСДВА, АДВСА, АДСВА. Их длины, соответственно, равны 25, 16, 21, 21,16, 25. Кратчайшими являются маршруты АСВДА и АДВСА. Существует еще один метод решения задачи коммивояжера - метод ветвей и границ. 49. Взвешенный граф. Граф-дерево. Определим понятие взвешенного графа. Сопоставим каждой вершине 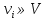 вес вес 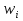 из множества весов W . В результате получим множество взвешенных вершин{ из множества весов W . В результате получим множество взвешенных вершин{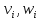 }, при этом не обязательно, чтобы все веса были различными. }, при этом не обязательно, чтобы все веса были различными.Аналогично сопоставим каждому ребру 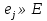 вес вес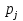 из множества весовP. В результате получим множество взвешенных ребер { из множества весовP. В результате получим множество взвешенных ребер {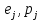 }. Определенные выше множества взвешенных вершин и ребер определяют в совокупности граф, взвешенный по вершинам и ребрам. }. Определенные выше множества взвешенных вершин и ребер определяют в совокупности граф, взвешенный по вершинам и ребрам.Опр. Н-граф называется неориентированным деревом (или просто деревом), если он связен и не содержит циклов, а значит, петель и кратных ребер. Дерево – это минимальный связный граф в том смысле, что при удалении хотя бы одного ребра он теряет связность. Наличие этих двух свойств (связность и отсутствие циклов) позволяет жестко связать число вершин и число ребер: в дереве с n вершинами всегда n -1 ребер. В этом графе 8 вершин и 7 ребер. Ни одно ребро нельзя удалить из графа без того, чтобы он не потерял связность. Деревом называется связный граф без циклов. Вот пример дерева (рис1): А вот пример графа, не являющегося деревом (рис 2): Рис 2. Рис1. 50. Цикломатическое число. Остов графа. Базис циклов. Пусть 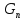 – связный граф. Остов(наименьший из всех графов, имеющий n вершин) этого графа содержит n-1 ребро. – связный граф. Остов(наименьший из всех графов, имеющий n вершин) этого графа содержит n-1 ребро.Если ранее в графе было N ребер, то удалить пришлось k=N-n+1 ребро. Величина k=N-n+1 называется цикломатическим числом связного графа. Цикломатическое число несвязного графа равно сумме цикломатических чисел связных компонент. Очевидно, что для любого графа–дерева это число равно нулю. Пусть G — произвольный (n, m)-граф с k компонентами связности. Если G — не дерево, то в нем (его компонентах связности) существуют циклы. Рассмотрим какой-либо цикл и удалим из него некоторое ребро. При этом количество компонент связности не увеличится. Если после этого еще останутся циклы, то рассмотрим следующий из них и снова удалим какое-либо его ребро. Продолжим этот процесс до тех пор, пока не исчезнут все циклы. Полученный в результате подграф, который, очевидно, является лесом и имеет столько же компонент связности, как и исходный граф G, называется остовом графа G. Базис циклов— базис пространства циклов графа, состоящий только из простых циклов. Базис циклов является максимальным набором независимых простых циклов графа или минимальным набором простых циклов, от которых зависят все циклы. 51. Двудольные графы. Опр. Граф G называется двудольным (или четным), если множество его вершин V распадается на два непересекающихся подмножества 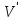 и и 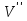 , таких, что каждое ребро графа G имеет один конец из , таких, что каждое ребро графа G имеет один конец из 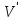 , а другой из , а другой из 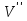 . .Для двудольных графов справедлива следующая теорема: граф Gявляется двудольным, если все его циклы имеют четную длину.
|