Элементами. Из определения следует, что элементы множества обладают двумя свойствами 1 вполне различимы 2
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Диаграммой состояний наз. ориентированный граф в котором количество вершин равно количеству состояний данного автомата и помечена символами внутренние cсостояние. Дуга выходящая из любой вершины qi помечается символами αt , βr . При этом: δ(αt , βr) = qi λ(αt , qi) = βr Автомат наз. инициальным, если он всегда начинает свою работу из одного и того же состояния и неинициальным если начинает свою работу с любого состояния. Автомат δ в общем случае является частичным и недетерминированным. Если D≤A×Q отображение Г , то автомат S всюду определенным и недетерминированным. Если задает функция отображения Г то всюду определенный и детерминированным. Поскольку автомат (1) задет функция (2) , то он относится к вектору определения детерминированного конечного автоматом. Если А=В={0,1} то автомат S наз. логическим автоматом. Автомат вида (1) наз. конечным автоматом Мили ( I рода) при этом поведение автомата (1) определяется парой функций qi(t)= δ(qi(t-1), qj(t)) bi(t)= λ(qi(t-1), qj(t)) qi(t-1), qj(t) - предыдущее и последнее состояние автомата. Автомат Мили – синхронный конечный автомат. Автомат II рода описывается функциями q(t)= δ(q(t-1), а(t)) b(t)= λ(q(t-1), а(t)) ! Для каждого автомата II рода сущ. эквивалентный ему автомат I рода. ! Между автоматами I и II рода сущ. взаимооднозначное соответствие. Примером автомата II рода может быть автомат Мура: q(t)= δ(q(t-1), а(t)) b(t)= λ( а(t)) Автомат Мура – автономный автомат без входа. 68.Дешифратор. Дешифратором наз. инициальный конечный автомат входным алфавитом которого явл. алфавит А={0,1}. На вход подается бесконечная последовательность символов данного автомата, а символ 1 печатается только в том случае, когда в данный момент устройство обозревает последовательность символов прочтенного слова α. При этом α – код комбинированных данных автомата. Неинициальный алфавит наз. сильно связным, если для каждого состояние автоматов qi, qj найдется точное слово α, что автомат начинает работу с состояния qi при считывании слова α перейдет в состояние qj . Состояния qi, qj неинициального автомата А1 и А2 наз. эквивалентными, если для любого слова α составляется из букв входного алфавита выводит слова полученные при работе автоматов А1 , А2 запущены из состояний qi, qj над словом α равны. Автоматы А1 и А2 эквивалентны, если для любого qi автомат А1 найдется эквивалентны ему qj автомат А2 , а так же для каждого qj* автомат А2 найдется эквивалентное ему сост. qi* автомата А1. Автомат Amin наз. минимальным для заданного автомата А если он эквивалентен автомату А и содержит наименьшее число внутренних состояний среди всех автоматов эквивалентных данному автомату А Автомат Мили наз. частичным автоматом, если хотя бы одна из функций перехода или выхода не явл. всюду определенной. 69.Реализация автоматов схемами. Функциональным элементом называется устройство, имеющее n упорядоченных отрезков вверху, которые называются входами, и один отрезок внизу, называемый выходом функционального элемента. Функциональный элемент изображается так: 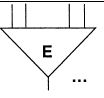 На входы функционального элемента могут подаваться сигналы двух типов, причём при подаче набора сигналов на входы элемента задержки, на выходе мгновенно возникает сигнал одного из этих типов, причём каждый набор входных сигналов однозначно определяет значение выходного сигнала. Элементом задержки называется конечный автомат, имеющий два внутренних состояния, входной и выходной алфавиты которого имеют по два символа и совпадают, и который осуществляет задержку входного сигнала на один такт времени. Элемент задержки изображается так: Верхний отросток называется входом, а нижний — выходом элемента задержки. Полюсами называется упорядоченный набор кружков, помеченных символами различных переменных. Схема из функциональных элементов и элементов задержки определяется индуктивно: 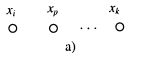 а) совокупность полюсов (кружков, помеченных символами переменных) есть схема; все полюсы являются её вершинами', б) результат присоединения к вершинам схемы всех входов некоторого элемента (функционального элемента или элемента задержки) есть схема; вершинами новой схемы являются все вершины исходной схемы и выход присоединённого элемента, а полюсами — все полюсы исходной схемы; 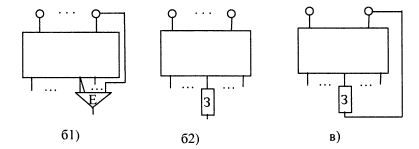 в) результат присоединения выхода задержки к некоторому полюсу xi есть схема; её вершинами являются все вершины исходной схемы, за исключением х-, а полюсами — все полюсы исходной схемы, кроме xi. Операция, соответствующая пункту в), называется введением обратной связи. 70. Ограниченно детерминированные функции. Информационные деревья. Если А- какой-либо алфавит, то пусть A* обозначает множество всех слов, а A0 - множество всех слов или множество всех сверхслов в алфавите А. Функция f, отображающая A0 в B0 , где Аи В- произвольные конечные алфавиты, наз. детерминированной функцией, если выполняются следующие два условия: 1) для любого α из A0 длина f(α) равна длине а 2)если-α слово длины l где α1 = αα’ , α2 = αα’’, α’, α’’Є A0 , то значения f(α1) и f(α2) имеют одинаковые начала длины l. Если детерминированная функция f определена на множестве 3) для любого слова α из A* и любого β из A0 справедливо равенство f(αβ) = f(α)fα(β), где f α - некоторая детерминированная функция на множестве A0 , однозначно определяемая словом α. Функция fa ,наз. остаточной функцией для f. Из условия 3) следует, что всякая детерминированная функция f определяет на множестве A* отношение эквивалентности R: αRβ тогда и только тогда, когда fα=fβ . Ранг этого отношения, или, что то же, максимальное число попарно различных остаточных функций, наз. весом детерминированной функции f. Если вес детерминированной функции конечен, то она наз. ограниченно-детерминированной функцией. Это понятие распространяется и на функции от т-переменных, где m≥2 если наборы из т-слов одинаковой длины (или сверхслов) в алфавитах A1, … , Am соответственно рассматривать как слова (сверхслова) в алфавите A1× … × Am , являющемся декартовым произведением алфавитов A1, … , Am . Таким же образом можно рассматривать О.-детерминированной функции с несколькими выходами, т. е. значениями которых являются наборы из к-слов или сверхслов соответственно в алфавитах B1, … , Bk Класс всех О.-детерминированной функции совпадает с классом функций, вычислимых конечными автоматами. Поэтому для задания О.-детерминированной функции могут быть использованы те же средства, что и для задания конечных автоматов, например, каноническое уравнения (см. Автомат конечный, Автоматов способы задания). Отсюда следует, в частности, что класс О.-детерминированной фунции с совпадающими алфавитами A1= … =Am = B замкнут относительно суперпозиций. Минимальный (по числу состояний) автомат U(A, S, B, φ, ψ, s1 ) вычисляющий О.-детерминированной функции f веса т, содержит п-состояний и может быть построен следующим образом. Пусть α1, …,αn - произвольные представители всех классов эквивалентности отношения R. Каждому классу R(αi), i=1, … , n , ставится в соответствие некоторое состояние si автомата U. Функция переходов j и функция выходов ψ определяются следующими условиями: если aЄA и 1≤ i ≤n, то φ(si, a)=sj , где состояние sj соответствует классу R(αi a); ψ(si, a)=fαi(a). В качестве начального берется состояние, соответствующее классу R(е), где е - пустое слово. 71. Понятие алгоритма. Основные свойства алгоритмов. Вычислимость. Под алгоритмом понимается способ преобразования представления информации. Основные особенности алгоритма:
Функция f с натуральными аргументами и значениями называется вычислимой, если существует алгоритм, её вычисляющий, то есть такой алгоритм A, что • если f(n) определено для некоторого натурального n, то алгоритм A останавливается на входе n и печатает f(n); • если f(n) не определено, то алгоритм A не останавливается на входе n. Несколько замечаний по поводу этого определения: 1. Понятие вычислимости определяется здесь для частичных функций (областью определения которых является некоторое под множество натурального ряда). Например, нигде не определённая функция вычислима (в качестве A надо взять программу, которая всегда зацикливается). 2. Можно было бы изменить определение, сказав так: «если f(n) не определено, то либо алгоритм A не останавливается, либо останавливается, но ничего не печатает». На самом деле от этого ничего бы не изменилось (вместо того, чтобы останавливаться, ничего не напечатав, алгоритм может зацикливаться). 3. Входами и выходами алгоритмов могут быть не только натуральные числа, но и двоичные строки (слова в алфавите {0, 1}), пары натуральных чисел, конечные последовательности слов и вообще любые, как говорят, «конструктивные объекты». Поэтому аналогичным образом можно определить понятие, скажем, вычислимой функции с двумя натуральными аргументами, значениями которой являются рациональные числа. 72. Рекурсивные функции. Операторы суперпозиции и примитивной рекурсии. Исходными функциями являются: 1) z(х) = 0 — нуль функция; 2) N(x) = х + 1 — функция следования: 3) Ik(x1,...,xn) = Xk k=1…n. —селекторная функция, (функция выбора аргумента, проектирующая функция) Из исходных функций образуются все остальные функции при помощи операций, которые наз. Функциональными операторами. Целочисленные компоненты вводятся как суперпозиции функций z(x) и N(x): N(z(x))=0+1=1 N(N(z(x)))=2 Функцию g(x)=x+z можно записать как: N(N(I1(x))) = (x+1)+1=x+2 Говорят, что функция n получается применением операции суперпозиции S, функция f,g1,…,gn при этом записывается так: h= S( f,g1,…,gn) если h(x1,...,xn)= f(g1( x1,...,xn),…, gn( x1,...,xn)) Говорят, что функция f зависящие от h+1 переменной получаются применением оператора примитивной рекурсии R к функция g(xn) и h(xn+1) если f=R(g,h): 1)f(x1,...,xn,0) = g(x1,...,xn) 2) f(x1,...,xn,k+1)=h(x1,...,xn,k,f(x1,...,xn,k)) k=N 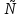 {0} {0}В данном случае рекурсия ведется по последней переменной и выражает уже известный способ математической индукции. Функция f называется примитивно-рекурсивной если она может быть получена из исходных функций применением конечного числа операторов суперпозиции и примитивной рекурсии. 73. Примитивно рекурсивные предикаты. Свойства. Предикат Р(х1,…,хn) называется примитивно рекурсивным если его характеристическая функция является примитивно рекурсивной. Характеристическая функция Xp (х1,…,хn )=0 или 1, 0 если Р(х1,…,хn)-ложно; 1 если Р(х1,…,хn) – истина Функция X рассматривается как функция натуральных элементов. Свойства: Опр.1 Если P,Q – примитивно рекурсивные предикаты, то ---P, P&Q, P 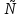 Q, P Q, P Q, P Q, P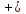 *Q , P *Q , P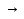 Q также примитивно рекурсивные предикаты Q также примитивно рекурсивные предикатыОпр.2 Пусть P1(х1,…,хn) , … , Pk(х1,…,хn) примитивно рекурсивные предикаты, причем Pi&Q j =0, для всех i 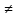 j, а P1 j, а P1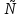 P2 P2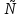 …. Pk …. Pk 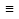 1 т.е при любом наборе переменной (х1,…,хn) только один из предикатов Pi i=1,k равен 1 и пусть функция g1(х1,…,хn)…. gk(х1,…,хn) примитивно рекурсивные предикаты Pi&Q j =0 функция f(х1,…,хn) = g1(х1,…,хn), P1 1 т.е при любом наборе переменной (х1,…,хn) только один из предикатов Pi i=1,k равен 1 и пусть функция g1(х1,…,хn)…. gk(х1,…,хn) примитивно рекурсивные предикаты Pi&Q j =0 функция f(х1,…,хn) = g1(х1,…,хn), P1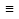 1 1 gk(х1,…,хn), Pk 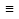 1,тогда функция также является примитивно рекурсивной 1,тогда функция также является примитивно рекурсивнойопр.3Если функция f(х1,…,хn,y) примитивно рекурсивная функция, то ограниченная сумма: g(x1,...,xn,a) = 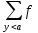 (х1,…,хn,y) и если f(х1,…,хn,0)=0 также является примитивно рекурсивной функция. (х1,…,хn,y) и если f(х1,…,хn,0)=0 также является примитивно рекурсивной функция.опр.4 Если функция f(х1,…,хn,y) примитивно рекурсивная функция, то ограниченное произведение g(x1,...,xn,a) = 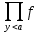 (х1,…,хn,y) при условии, что f(х1,…,хn,0)=1 также является примитивно рекурсивной функцией. (х1,…,хn,y) при условии, что f(х1,…,хn,0)=1 также является примитивно рекурсивной функцией.опр.5 Если P(х1,…,хn,y) примитивно рекурсивный предикат, то огранич кванторы Q1(х1,…,хn,a) = 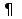 y P(х1,…,хn,y) в случае если P(х1,…,хn,0)=1 а также Q2(х1,…,хn,a) = y P(х1,…,хn,y) в случае если P(х1,…,хn,0)=1 а также Q2(х1,…,хn,a) =  y P(х1,…,хn,y). y P(х1,…,хn,y).Если P(х1,…,хn,0)=0 также, является примитивно рекурсивными предикатами. 74. Классы рекурсивных функций. (п.р., о.р., ч.р.). Тезис Черча. Функция f(х1,…,хn,z) называется результатом примитивно ограниченный оператор минимизации ( 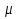 -оператор) к предикату P(х1,…,хn,y), если функция f равна такому значению у = {0,1…z} при котором значение предиката Р(х1,…,хn,y) = 1 а для -оператор) к предикату P(х1,…,хn,y), если функция f равна такому значению у = {0,1…z} при котором значение предиката Р(х1,…,хn,y) = 1 а для 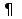 t t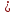 y значение предиката Р(х1,…,хn,y)=0 y значение предиката Р(х1,…,хn,y)=0В этом случае записывают: f(х1,…,хn,z)= 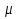 yP(х1,…,хn,y) yP(х1,…,хn,y)Теорема: Если Р(х1,…,хn,y) примитивно рекурсивный предикат, то функция 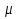 yP(х1,…,хn,y) является примитивно рекурсивной yP(х1,…,хn,y) является примитивно рекурсивной |
