Элементами. Из определения следует, что элементы множества обладают двумя свойствами 1 вполне различимы 2
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
, → . |
P-символ предиката.
1) x1,…,xn–предикатные переменные, то P(x1,…,xn) –n-местный предикат и все его переменные свободны.
2) Если A-предикатная формула, то
 – так же предикатная формула с тем же набором свободных переменных.
– так же предикатная формула с тем же набором свободных переменных.3) Если A,B– предикатные формулы и нет переменных свободных в одной формуле и связанных в друг., то формулы A&B, A˅B , A
| X1 | X2 | X3 | X4 | f |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| |   x4 x4 |  x3 x4 |  x2 x2 x4 x4 |  x2 x2x3 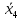 | x1   x4 x4 | x1  x3 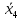 | x1 x2  | x1 x2 x3 x4 |
  x4 x4 | |  x4 |  x4 | | 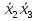 x4 | | | |
 x3 x4 |  x4 | | | | | | | |
 x2 x2 x4 x4 |  x4 | | | | | | | |
 x2 x2x3 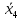 | | | | | | | | |
| x1   x4 x4 | 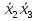 x4 | | | | | | | |
| x1  x3 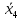 | | | | | | | | |
| x1 x2  | | | | | | | | |
| x1 x2 x3 x4 | | | | | | | | |
| | ⌐x1⌐ x2⌐ x3 x4 | ⌐x1⌐x2 x3 x4 | ⌐ x1 x2⌐x3 x4 | ⌐x1 x2 x3 ⌐x4 | x1⌐x2⌐ x3 x4 | x1⌐x2 x3 ⌐ x4 | x1 x2⌐x3 ⌐ x4 | x1 x2 x3 x4 |
| ⌐x1⌐x2 x4 | Ӿ | Ӿ | | | | | | |
| ⌐x1⌐x3 x4 | Ӿ | | Ӿ | | | | | |
| ⌐x2⌐ x3 x4 | Ӿ | | | | Ӿ | | | |
⌐x1⌐x2x4 ˅⌐x1x2⌐x3 x4 ˅x1⌐x2⌐x3 x4
35.Построение Сокращенных ДНФ геометрическим методом. Пример.
Установим геометрический смысл простой склейки с точки зрения "геометрии" булева куба. Простая склейка может быть применена только к таким двум элементарным конъюнкциям Ka и Kb, соответствующим наборам переменных a и b, что для некоторого i
a = (a1, a2,..., a i – 1, a i, a i + 1, …, an),
b = (a1, a2,…, a i – 1, ¬a i, a i + 1, …, an).
Это значит, что наборы a и b таковы, что один из них доминирует над другим (они различаются значением только одной компоненты, значит a ≤ b или b ≤ a), т.е. они образуют ребро булева куба Вn. Следовательно, простой склейке, применяемой к элементарным конъюнкциям исходной СДНФ, представляющей функцию, подлежат те и только те элементарные конъюнкции, которые соответствуют элементам какого-либо ребра булева куба, на котором функция принимает единичное значение. Образно говоря, две соседние вершины куба, на которых функция равна 1, "склеиваются" в ребро, их "соединяющее".
Пример:
F(x,y,z)=(01101110)
| x | y | z | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
(Нарисовать куб)
Nf={(001),(010),(100),(101),(110)}
ДНФ= ⌐x⌐yz˅⌐xy⌐z˅x⌐y⌐z˅x⌐yz˅xy⌐z
СДНФ=x⌐z˅⌐yz˅⌐xy⌐z
36. Построение минимальных ДНФ с помощью карт Карно.
Метод минимизаций карт Карно:
Применяется для построения СДНФ функций четырех переменных.
В этом методе для функции f(
 4) составляется таблица размером 4*4 каждая клетка которой соответствует вершине четырехмерного куба, причем соответствия зад. Таким образом, что если склеить карту по вертикали и горизонтали, то соседние карты клетки будут соответствовать соседним вершинам куба.
4) составляется таблица размером 4*4 каждая клетка которой соответствует вершине четырехмерного куба, причем соответствия зад. Таким образом, что если склеить карту по вертикали и горизонтали, то соседние карты клетки будут соответствовать соседним вершинам куба.Клетка в таблице соответствующая вершинам куба в котором функция принимает значение 1 ставят Ӿ.
Гранью называют множество Ӿ карты соответствующей какой-либо грани четырехмерного куба.
Мощность грани – количество Ӿ.
Максимальной гранью для каждой Ӿ будем считать грань с наибольшей мощностью.
Полезной мощностью будем называть множество еще непокрытых Ӿ данной грани (0,1,2,…,m)(m-максимальная мощность грани)
Пример:f(
 4)=(0010101001010111)
4)=(0010101001010111)-
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
-
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
Ӿ
37. Метод Нельсона. (Построение сокращенной ДНФ с помощью КНФ).
Суть метода: в КНФ раскрываются скобки и удаляются дублирующие члены, затем удаляем те дизъюнктивные слагаемые, которые содержат одновременно и переменную и ее отрицание. В полученном выражении удаляют все нулевые диз. слагаемые, проводят все поглощения и удаляют дублирующие члены. A˅A*B=A (поглощение)
Пример:
 (
( )(
)(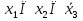 )
)Найдем СДНФ:
 =
=
Произведем поглощения :
 - СДНФ
- СДНФ 38.Построение всех тупиковых ДНФ. Алгоритм минимизации функций в классе нормальных форм.
Пусть f(x1, …, xn) – булева функция
1)находим табл. Значения функции f(x1, …, xn)=(101…01)
2)по табличным значения строим СДНФ функции f
3)строим СДНФ f=K1Ú K2Ú …Ú Km где Ki -простые импликанты
4)строим матрицу покрытий простых импликант функции f
5)для каждого столбца 1 ≤ j ≤ k находим множество Ejномеров строк для которых aj = 1 составляем множество
 =(
=(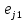 ,
, 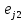 , … ,
, … ,  ), где
), где  импликанты соответствующие значение 1. Получаем выражение A=
импликанты соответствующие значение 1. Получаем выражение A=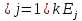 назыв. Решеточным покрытием ДНФ ф-ции f. Удаляем все дублирующеюся символы получаем ТДНФ.
назыв. Решеточным покрытием ДНФ ф-ции f. Удаляем все дублирующеюся символы получаем ТДНФ.39. Понятие о функциях k-значной логики. Их особенности.
Функция f(х1,х2,…,хn) аргументы которой определены на мн-ве Ek = {0, 1, 2, …, k – 1} назыв. функцией k-значной логики.
Произвольная n-местная функция к-значной логики может быть задана с помощью таблицы следующей:
В этой таблице kn – строк. Рк – множество всех
| х1 | … | xn-1 | xn | f (x1,…,xn-1,xn) |
| 0 | … | 0 | 1 | f (0,0,…,0) |
| 0 | … | 0 | 1 | f (0,0,…,1) |
| …… | … | …… | …… | ……. |
| 0 | … | 0 | k-1 | …… |
| …… | … | …. | …… | ….. |
| k-1 | ……. | k-1 | k-1 | f (k-1, k-1,…, k-1) |
функций к-значной логики. Рк(n) – множество функций из Рк, зависящих от n-переменной.
Множество всех функций k-значной логики будем обозначать
 . В Pk часто употребляется задание таких функций, при помощи алгоритма вычислимости функций.
. В Pk часто употребляется задание таких функций, при помощи алгоритма вычислимости функций.Следующие функции к-значной логики считаются элементарными:
Константы 0, 1, …, k-1
Отрицание Поста :
: 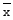 =x+1 mod k.
=x+1 mod k. 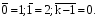
Отрицание Лукашевича x = k-1-х;
Характеристическая функция 1го рода ;
;
Характеристическая функция 2го рода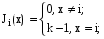 (возведение в степень);
(возведение в степень);
xÙy = min{x,y}
xÚy=max{x,y}.
Сумма по модулю k x+y=(x+y) mod k;
Усеченная разность:
Импликация (x содержит в себе y) x y=
y=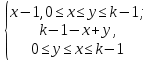
 - функция Вебба.
- функция Вебба.
Разность: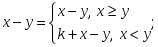
Пусть E
 будем говорить, что ф-ция f-сохраняет множество E, если "
будем говорить, что ф-ция f-сохраняет множество E, если "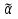 =(
=(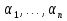 ), таком, что
), таком, что 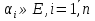 значения ф-ции
значения ф-ции 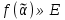 . Множество всех функций Pk ,сохраняющих мн-во E обозначим
. Множество всех функций Pk ,сохраняющих мн-во E обозначим 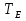 .и называется классом функций, сохраняющих множество Е. Очевидно, что класс ТЕ является замкнутым.
.и называется классом функций, сохраняющих множество Е. Очевидно, что класс ТЕ является замкнутым.40.Графы. Изоморфизм графов.
Графом G называется совокупность двух мн-в G=(V, E), где V- мн-во вершин графа, а Е –мн-во ребер графа. Между вершинами и ребрами графа G устанавливают отношение инцидентности. Считают, что ребро
 инцидентно вершинам
инцидентно вершинам 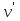 ,
, 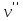 если оно соединяет эти две вершины. При этом вершины
если оно соединяет эти две вершины. При этом вершины 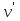 ,
, 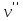 называются смежными.
называются смежными.Отношения инцидентности являются самым главным элементом графа, т.к. указывается способ объединении v и e в единый объект.
Ребра инцидентные одной и той же паре вершин назыв. кратными. Граф содер. Кратные ребра назыв. мультиграфом.
Ребро(дуга) концевые вершины которого совпадают назыв. узлом.
Вершина неинцидентная ни одному ребру назыв. изолированной.
Если граф состоит только из изолированных вершин, то он назыв. нульграфом.
Граф без петель и кратных ребер назыв. полным, если каждая его вершина соединена ребром.
Дополнением графа G называется граф
 имеющий те же вершины что и граф G и содержащий только те ребра которые нужно добавить к G, что бы получался полный граф.
имеющий те же вершины что и граф G и содержащий только те ребра которые нужно добавить к G, что бы получался полный граф.Локальной степенью вершины v
 n-графа G называется число
n-графа G называется число  равное кол-ву ребер инцидентных вершине v. В n-графе сумма всех степеней равна удвоенному числу ребер графа, т.е.
равное кол-ву ребер инцидентных вершине v. В n-графе сумма всех степеней равна удвоенному числу ребер графа, т.е. ,
, 
Для вершин ор-графа определяют две локальные степени
 и
и  , где
, где  -кол-во дуг исходящих из вершины v,
-кол-во дуг исходящих из вершины v,  - кол-во дуг входящих в вершину v.
- кол-во дуг входящих в вершину v.Петля дает вклад 1 в обе эти степени. В ор-графе суммы этих степеней

Графы G=(V,E) и G'=(V',E') изоморфны (пишут G
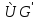 ), если существует взаимно-однозначное соответствие между множествами Vи V', сохраняющее смежность вершин (т.е. такое соответствие, при котором вершины vi и vj из множества Vсмежны тогда и только тогда, когда смежны соответствующие им вершины
), если существует взаимно-однозначное соответствие между множествами Vи V', сохраняющее смежность вершин (т.е. такое соответствие, при котором вершины vi и vj из множества Vсмежны тогда и только тогда, когда смежны соответствующие им вершины 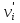 и
и 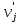 из множества V')
из множества V')41.Способы задания графов.
Способы задания графов:
Графический способ
Задание графа при помощи матрицы инцидентности
 n
n m – где n кол-во вершин графа, m – кол-во ребер графа. По вертикали и горизонтали указываются вершины и ребра, а на пересечении i-строки и j-столбца, если ребро i инцидентно вершине j ставим 1 и 0 в противном случае.
m – где n кол-во вершин графа, m – кол-во ребер графа. По вертикали и горизонтали указываются вершины и ребра, а на пересечении i-строки и j-столбца, если ребро i инцидентно вершине j ставим 1 и 0 в противном случае.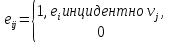
В случае орграфа

В петле присваивается любое другое число!!! (чаще всего 2)
Списком ребер графа
Список ребер графа представл. столбцом. В левом столбце перечисляется все ребра, а в правом инцидентные ему вершины, причем для n-графа порядок написания вершин произвольный, а для ор-графа первым стоит номер начала дуги.
Если граф имеет изолированные вершины, то они помещаются в конец списка.
Матричный способ:
Матрица смежности - это квадратная матрица
 размера
размера 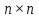 , где n – кол-во вершин графа.
, где n – кол-во вершин графа.В случае n-графа проставляется число ребер соединяющих эти две вершины.
В случае ор-графа проставляется кол-во дуг имеющих начало в вершине
 и конец в вершине
и конец в вершине  .
.Определение 2.21. Матрицей смежности конечного графа G с p вершинами называется матрица A(G)=||aij|| (i, j = 1, 2, …, p), в которой если смежны вершины то ставим 1, иначе 0.
42. Действия над графами.
Граф H будем называть

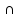 [B UC] = [A
[B UC] = [A )-(m(A
)-(m(A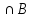 )+m(A
)+m(A ).
). 29.
29. )
)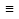 1. Аналогичная формула называется тождественно ложной, если эта формула выражает булеву функцию f(
1. Аналогичная формула называется тождественно ложной, если эта формула выражает булеву функцию f( 0. Опровержима, если f(
0. Опровержима, если f( .
.  .
. 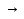 (B
(B )
) (A
(A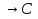 )).
)).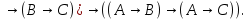
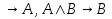 .
. 
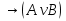 ; B
; B ).
).  )
) A)
A)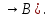
 .
.  Pi=1,i=
Pi=1,i= ; P1&…&Pn=1;1
; P1&…&Pn=1;1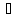 А:
А: 
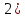 Г
Г
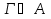 )&(Г
)&(Г )&(АВ
)&(АВ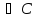 )
) )&(
)&(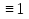 .
. 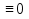 .
.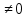 ; опровержимой, если f(
; опровержимой, если f( .
.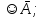
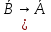 )→((
)→(( )→B);
)→B); ,& , ˅ ,
,& , ˅ ,  А1 -А4 – совпадают с соответствующими аксиомами исчисления высказываний. А5 , ∀xi (P(xi)→P(xk)) если P(xi) не содержит переменной xk A6 , P(xi)→∃xk(P(xk))
А1 -А4 – совпадают с соответствующими аксиомами исчисления высказываний. А5 , ∀xi (P(xi)→P(xk)) если P(xi) не содержит переменной xk A6 , P(xi)→∃xk(P(xk)) j
j (полное склеивание)
(полное склеивание) (неполное склеивание)
(неполное склеивание)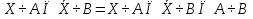 (обобщенное склеивание)
(обобщенное склеивание)