Элементами. Из определения следует, что элементы множества обладают двумя свойствами 1 вполне различимы 2
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
52. Планарные графы. Критерий планарности. Говорят, что граф G укладывается на плоскости, т. е. является планарным, или плоским, если его можно нарисовать так, что его ребра будут пересекаться лишь в концевых точках – вершинах. Изображение планарного графа на плоскости называется планарной укладкой. 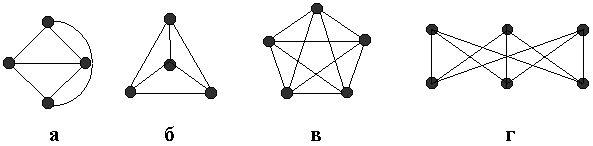 Рис. 1.24. Примеры планарного и непланарных графов: а - планарная укладка с непрямолинейными ребрами; б - планарная укладка того же графа с прямолинейными ребрами; в - непланарный граф K5; г - непланарный граф K3,3 Теорема. Граф планарен тогда и только тогда, когда он не содержит в качестве подграфа графа 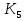 или или 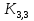 .До появления этой теоремы определение планарности графа считалось одной из труднейших задач теории графов. .До появления этой теоремы определение планарности графа считалось одной из труднейших задач теории графов.На рис. 1.25 приведен непланарный граф Петерсена. 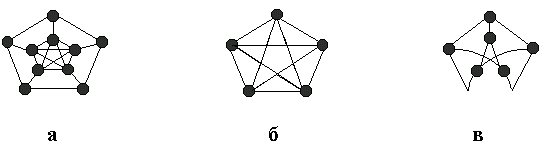 Рис. 1.25. Непланарность графа Петерсена: а - граф Петерсена; б - граф Петерсена, стянутый к K5; в - один из подграфов графа Петерсена, гомеоморфный K3,3 Граф Петерсена не имеет подграфов, гомеоморфных K5, но легко стягивается к K5. Сложнее увидеть, что граф Петерсена имеет подграф, гомеоморфный K3,3. 53. Теорема Куратовского-Понтрягина. Граф Петерсена. 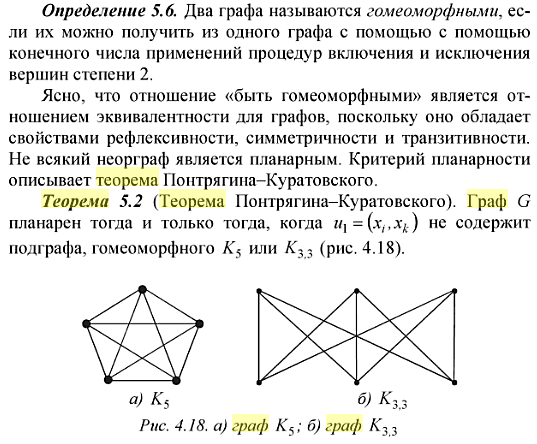 Доказательство: необходимости. С геометрической точки зрения, добавление вершины степени 2 — это добавление точки на ребре, а стирание такой вершины объединяет два ребра с общим концом в одно. Очевидно, что любая из этих операций, примененная к плоскому графу, снова даст плоский граф. Значит, по следствиям из теоремы Эйлера, никакой плоский (а следовательно, и планарный) граф не гомеоморфен графам K5 и K3,3. С учетом замечания о непланарных подграфах, необходимость доказана. Граф Петерсена 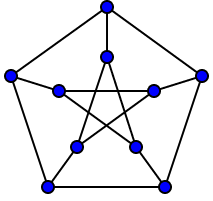 54.Двухполюсные сети. Параллельно-последовательные сети. Поток в сети. Опр. (k,l) – полюсником называется сеть имеющая k+l полюсов разбитых на два класса: k-входных полюсов, l – выходных полюсов. (1,1)-полюсник называется двухполюсной сетью. Цепью называют простую цепь между полюсами сети(S). 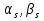 – входной, выходной полюс. Полюсные ребра-Z. – входной, выходной полюс. Полюсные ребра-Z.Сеть состоящая из n параллельных ребер, соединяющих полюса 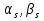 обозначается через обозначается через 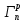 . .Сеть, которая может быть получена из сетей  и и 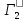 применением конечного числа операций подстановки сети вместо ребра называется параллельно-последовательной сетью. применением конечного числа операций подстановки сети вместо ребра называется параллельно-последовательной сетью.Опр. Сетью называется связный ориентированный граф G(V, E) без петель с выделенными вершинами 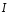 истоком и истоком и 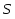 стоком, причем каждой дуге поставлено в соответствие некоторое натуральное число стоком, причем каждой дуге поставлено в соответствие некоторое натуральное число 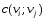 – пропускная способность дуги. – пропускная способность дуги.Пропускная способность дуги характеризует максимальное количество вещества, которое может пропустить за единицу времени дуга 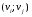 . Договоримся на сети пропускную способность дуги записывать в круглых скобках. . Договоримся на сети пропускную способность дуги записывать в круглых скобках.Поток в сети определяет способ пересылки некоторых объектов из одной вершины графа в другую по направлению дуги. Число объектов (количество вещества) 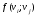 , пересылаемых вдоль дуги , пересылаемых вдоль дуги 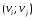 , не может превышать пропускной способности , не может превышать пропускной способности  этой дуги: этой дуги: 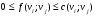 . Будем считать, что если существует дуга из . Будем считать, что если существует дуга из 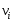 в в 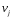 , то нет дуги из , то нет дуги из 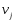 в в 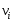 . Таким образом, рассматривается поток вещества только в одну сторону. . Таким образом, рассматривается поток вещества только в одну сторону.55.Теорема Форда-Фалкерсона о максимальном потоке. Расчет максимального потока в сети. Теорема: для любой сети с одним источником и одним стоком макс величина потока fmax через эту сеть равна мин из пропускных способностей cmin её простых сечений. Алгоритм нахождения макс потока: 1 этап(расчёт полного потока):предположим что в сети f имеется некоторый путь из αsв βs и поток вдоль этого пути, путь содержит ненасыщенные дуги. Значит, поток можно увеличить на величину Δ равную минимуму из остаточных пропускных способностей дуг входящих в этот путь. Перебирая все возможные пути из αs в βs и проводя такую же процедуру увеличением потока пока это возможно получим полный поток для которого каждый путь из αs содержит по крайней мере одну насыщенную дугу. 2 этап(расчет макс потока):рассмотрим сеть в которой уже построен полный поток. Берем произвольный путь из х1х6. Дуги образующие этот маршрут делятся на прямые и обратные. Если существует путь в котором прямые дуги не насыщенные, а потоки на обратных дугах положит, если Δ1 минимальный из остаточных пропускных способностей прямых дуг, а Δ2 минимальный из величин потоков отрицательных дуг, величину потока в этой сети можно увеличить на величину Δ, прибавляя это значение к потокам на прямых дугах и отнимая эту величину от обратной длины. 56.Общие принципы помехоустойчивого кодирования. Примеры. Пусть имеется канал связи С, содержащий источник помех: S→S’, S из A*, S’ из D*, где S- множество переданных, а S*- множество принятых по каналу сообщений. Кодирование F, обладающее таким св-вом что: 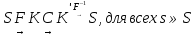 , ,F-1(C(F(s)))=S называется помехоустойчивым. Далее будем считать, без потери общности, что A=D={0,1} и что содержательное кодирование выполняется на устройстве, свободном от помех. Кодирование с исправлением ошибок представляет собой метод обработки сообщений, предназначенный для повышения надёжности передачи по цифровым каналам. Свойства: 1. Использование избыточности: закодированная последовательность всегда содержит дополнительные, или избыточные, символы. 2.св-во усреднения, означающее, что избыточные символы зависят от нескольких информационных символов.  57.Типы ошибок. Сжатие информации. Типы ошибок: 1. 0→1, 1→0 – ошибка типа замещения разряда. 2. 0→ᴧ - ошибка типа выпадения разряда. 3.ᴧ→0, ᴧ →1 - ошибка типа вставки разряда. Опр: методы кодирования, которые позволяют построить(без потери информации) коды сообщений, имеющие меньшую длину по сравнению с исходным сообщением, называются методами сжатия(или упаковки) информации. Качество сжатия обычно определяется коэффициентом сжатия, измеряется в процентах и показывает, насколько сжатое сообщение короче исходного. Способ кодирования: 1. исходное сообщение по некоторому алгоритму разбивается на последовательность символов, называется словами. 2. полученное множество считается буквами нового алфавита. Для этого алфавита строится разделимая схема алфавитного кодирования. Полученная схема обычно называется словарём, так как сопоставляет слову код. 3.Далее код сообщения строится как пара-код словаря и последовательность кодов слов из данного словаря. 4.При декодировании исходное сообщение восстанавливается путём замены кодов слов на слова из словаря. 58.Код Хэмминга. Зафиксируем число n, вычислим l такое, что 2l-2≤n≤2l, т.е. l=[  ]=1. Для произвольного слова Х=х1х2…хn ]=1. Для произвольного слова Х=х1х2…хn вычислим H(x)=x1el(1) вычислим H(x)=x1el(1)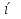 … …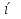 xnel(n)- вектор полученный в результате сложения векторов el(i), является двоичными кодами номеров единичных символов слова х. xnel(n)- вектор полученный в результате сложения векторов el(i), является двоичными кодами номеров единичных символов слова х. Теорема(Код Хэмминга): Hn состоящий из всех слов Х=х1х2…хn  , таких, что Hn(х)=(0,0,..,0) является кодом с исправлением одного замещения. |Hn|- число элементов кода |Hn|=2n-1, причём компоненты или позиции соответствующие 20,21,22,…,2l-1 наз. проверочными позициями. Позиции отличные от проверочных называются информационными. , таких, что Hn(х)=(0,0,..,0) является кодом с исправлением одного замещения. |Hn|- число элементов кода |Hn|=2n-1, причём компоненты или позиции соответствующие 20,21,22,…,2l-1 наз. проверочными позициями. Позиции отличные от проверочных называются информационными. Суть метода Хэмминга в том, что кодируемое слово длины n дополняется l проверочными разрядами, которые определяются образом высчитывания при кодировании. В итоге передаёт слово, длины m+l, где проверочные символы стоят на 20,21,22,…,2l-1месте. 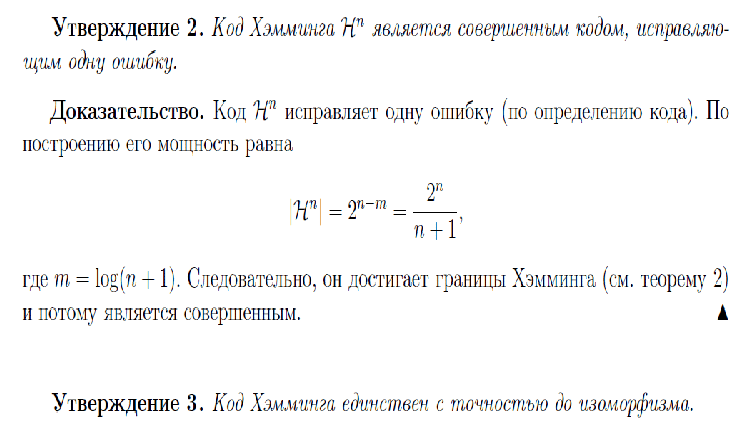 Пример.'>59.Троичный код Хэмминга. Пример. Расширенный код Хэмминга(EHml) получен из двоичного кода Хэмминга добавлением бита проверенного на чётность, минимальное расстояние в таком коде увеличивается до 4, т.е. полученный код исправляющий одну ошибку и обнаруживающий 2 ошибки. Код Хэмминга может быть распространён на любое конечное поле Fq. Выберем произвольно l и построим проверочную матрицу для линейного кода Fq с избыточностью b исправляемую одну ошибку, добавлением каждый новый столбик будем проверять, что он ЛНЗ от ранее выбранного столбца. 1.Выберем q0=1 столбцов, когда столбец выбран, удаляем из дальнейшего рассмотрения не только этот столбец, но и все его q-1 кратных столбцов. Получим, что 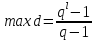 . Построен таким образом минимальный код Hml(p) имея избыточность если существует проверочная матрица семейства столбцов. . Построен таким образом минимальный код Hml(p) имея избыточность если существует проверочная матрица семейства столбцов. Теорема: Код Хэмминга избыточности 1 над полем Fq является линейным:  является совершенным кодом исправляющим ошибку. является совершенным кодом исправляющим ошибку.Док-во: Длина кода n= 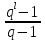 , т.к. код имеет избыточность l, то его размерность n-l, значит граница Хэмминга определяется условиями qn-l(1+(q-1)n)≤qn, qn-l(1+(q-1) , т.к. код имеет избыточность l, то его размерность n-l, значит граница Хэмминга определяется условиями qn-l(1+(q-1)n)≤qn, qn-l(1+(q-1)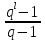 )=qn-lql=qn≤qn код является совершенным. )=qn-lql=qn≤qn код является совершенным.Задача: Рассмотри троичный [13,10] код Хэмминга 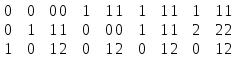 Декодировать (2,2,2,2,2,2,1,1,1,1,1,1,1) Х=(11001), |Х|=5, l=[ 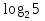 ]+1=4 и ещё построить таблицу и найти проверочные элементы. ]+1=4 и ещё построить таблицу и найти проверочные элементы.60.Алфавитное кодирование. Постройка кода, когда кодируется каждая буква алфавита А={а1,а2,…} называется алфавитным кодированием. Пусть α=α1α2 некоторое слово, тогда α1 называется префиксом(началом слова), а α2-постфиксом(конец слова). Алфавитное кодирование задаётся схемой: δ=(α1→β1,…,αn→βn) где αi 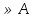 , βi , βi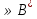 . Множество слов V={βi |βi . Множество слов V={βi |βi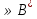 }, i=1,n называется множеством элементарных кодов. }, i=1,n называется множеством элементарных кодов. Алфавитное кодирование можно использовать для любого множества сообщений S. F:A*→B* ,если F(α)=(βi1,…,βik), где α=(αi1,…,αik). Пример: А={0,1,2,3,4,5,6,7,8,9} B={0,1} δ1={0→0, 1→1, 2→10, 3→11, 4→100, 5→101, 6→110, 7→111, 8→1000, 9→1001}. Пример: А={0,1,2,3,4,5,6,7,8,9} B={0,1} δ2={0→0000, 1→0001, 2→0010, 3→0011, 4→0100, 5→0101, 6→0110, 7→0111, 8→1000, 9→1001}. Схемы δ1и δ2 являются однозначными, но δ1не является взаимно-однозначным соответствием, а кодирование по схеме δ2 является взаимно-однозначным. Схема алфавитного кодирования δ называется разделимой, если любое слово, составленное из элементов кодов единственным образом, разбивается на эти элементарные коды. Алфавитное кодирование с разделимой схемой допускает декодирование. Теорема: Префиксная схема является разделимой. Для того чтобы схема алфавитного кодирования была разделимой необходимо, чтобы длина элементарных кодов удовлетворяла неравенству Макмиллана: 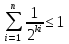 , где ki=|βi|. , где ki=|βi|.61. Алгоритм Фано.Пример Метод кодирования Фано заключается в следующем: упорядоченной в порядке убывания системе букв приписываются действия. 1) Список букв делиться на две части a1……..ak, ak+1…….an. таким образом, чтобы суммы вероятностей обеих частей как можно меньше отличались друг от друга. 2) Буквам первой части приписывается символ 1,буквам второй части – 0.Далее точно также поступают с оставшимися частями. Процесс продолжается до тех пор, пока весь список не разделится на части, каждая из которых состоит из 1 – ой части. 3)Каждой букве ставится в соответствие последовательность из 1 и приписанных в результате деления. Каждая буква ai получает свой код, который является префиксным. Метод Фано позволяет построить префиксный код, стоимость которого очень близка к оптимальной. ПРИМЕР: Рассмотрим алфавит, состоящий из 7 букв. A={a1, a2, a3, a4, a5, a6, a7,} Даны вероятности уже в порядке убывания: P={0,2; 0,2; 0,19; 0,12; 0,11; 0,09; 0,09}.
62. Алгоритм кодирования Хаффмена.Пример Лемма: Пусть G=(αi->βi), где i=1 до i=n; схема оптимального кодирования для вероятности p, где p1≥p2≥…≥pn 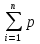 I .Тогда если pi >pa , то ki <= kk . I .Тогда если pi >pa , то ki <= kk .Теорема: Пусть Gn-1=(αi->βi), где i=1 до i=n-1 схема оптимального префиксного кодирования. Пусть при этом pj = q/+q//, тогда p1≥p2≥…≥pj-1≥pj+1≥….≥pn-1≥ q/≥ q//>0. Тогда кодирование имеющие Gn=( α1->β1,…, αj-1->βj-1 ,…, αj+1->βj+1,…., αn-1->βn-1) Тогда кодирование с такой схемой, является оптимальным префиксным кодированием с системой P: p1,….,pj-1, pj+1,…, pn-1, q/, q//. Данная теорема определяет способ построения алгоритма кода. Для списка вероятностей упорядоченного по убыванию убирают две последние вероятности. Вероятности, а их список составляют так, чтобы он был упорядочен по убыванию, на втором шаге вновь выбрасывают две последние вероятности, а их сумма вставляется в преобразованный список так, чтобы он оставался упорядоченным по убыванию. Первой вероятности принимают символ 0, второй символ 1. Далее согласно теореме из оптимального кода для двух букв строиться оптимальный код для трех букв и т.д. до тех пор, пока не получится исходный код исходного списка вероятностей. Пример: 0,2 0,2 0,23 0,37 0,4 0,6 0 0,2 0,2 0,2 0,23 0,37}00 0,4 1 0,19 0,19 0,2 0,2} 10 0,23}01 0,11 0,18 0,19} 000 0,2}11 0,09} 0010 0,12}010 0,18}001 0,09} 0010 0,11}010 } – показывается сумма! | |||||||||
