Элементами. Из определения следует, что элементы множества обладают двумя свойствами 1 вполне различимы 2
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Результатом применения неограниченного оператора минимизации к предикату Р называется функция f=1 равную значению y=N 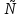 {0}. А для {0}. А для  t t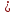 y равно P=0. Если такое значение у не существует, то функция f является неопределенной. y равно P=0. Если такое значение у не существует, то функция f является неопределенной.Опр: Функция называется частично рекурсивной, если она может быть получена из исходных, применением конечного числа операторов S, конечного числа операторов примитивно рекурсии и конечного числа неограниченного 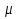 - операторов - операторовТезис Черча : всякая эффективно вычислимая функция является частично рекурсивной 75. Машины Тьюринга. Принципы работы. Протокол работы. Машиной Тьюринга Т называется тройка множеств T= Р = РТ = {T(i,j) | i=1,…,n; j=0,1,…,m} – программа машины Т; где Т(i,j) – команды этой программы, причем, для каждой пары (i,j) существует одна единственная команда Т(i,j), которая имеет один из видов: qiaj 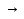 qkal qiaj qkal qiaj 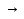 qkR qkR qiaj 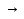 qkL qkLПринцип работы. МТ представляет собой бесконечную в обе стороны ленту разбитую на ячейки причем имеется конечное число упорядоченных ненулевых символов. В начальный момент времени в ячейке вписаны символы из алфавита А, в остальные ячейки вписаны пустые символы, которые обычно обозначаются 0. МТ имеет считывающе-пишущую головку, которая в любой момент времени обозревает заданную ячейку и воспринимает в этой ячейке символ. В момент времени к головка находится в левой части. Если МТ находится в состоянии символов qi а в обозрев ячейке находится аj , то выполняется команда qkajS. Для МТ начальным символом, является состояние q1 q0 считается конечным символом или заключительным состоянием машины Тьюринга. МТ останавливается если в левой части цепочки отсутствует символ q0 и останавливается, также если отсутствует команда которую необходимо выполнить, такого вида остановка считается безрезультативной. Конфигурацией МТ будем называть слово К вида UqiV , гдеU-слово на ленте левее голов, а V- слово на ленте правее. Если при выполнении команды получается что из конфигурация ki получаем кофигурацию kj то записывают: T: Ki 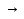 Kj KjЕсли Т: К1  К2 К2 К3 К3 … … Кn то Т: К1=> Кn Кn то Т: К1=> КnЕсли К1и Кn – начальные и конечные конфигурации, то записывают так: Т: К1|- Кn Детерминированная последовательность К1 К2К3…Кn….. называют протоколом работы МТ Говорят что МТ Т применяется к слову А, если Т начиная работу над словом А останавливается через конечное число шагов. Если в результате работы получается слово В, то записывают Т(А)=В. Если МТ не останавливается, то говорят, что Т не применимо к слову А. 76.Машины Тьюринга. Примеры. Функции, вычислимые по Тьюрингу. Машиной Тьюринга Т называется тройка множеств T= Р = РТ = {T(i,j) | i=1,…,n; j=0,1,…,m} – программа машины Т; где Т(i,j) – команды этой программы, причем, для каждой пары (i,j) существует одна единственная команда Т(i,j), которая имеет один из видов: qiaj 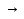 qkal qiaj qkal qiaj 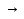 qkR qkRqiaj 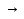 qkL qkLпример: рассмотрим МТ : Т: q1а 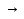 qbR, q1b qbR, q1b  q2 aR, q2а q2 aR, q2а  q0, q2b q0, q2b  q1L A={a,b} q1L A={a,b}Рассмотрим работу МТ над конфигурациями 1) q1aa … 0 0 q1а 0 … … 0 b a q2 0 … … 0 b a q0 0 … T(a,a)=ba (T: aa|- ba) 2) q1 ab … 0 a q1b 0 … … 0 b bq1 0 … … 0 bq1 b 0 … … 0 a bq2 0 … … 0 a q1b 0 … T не применимо к слову ab МТ Т можно задавать при помощи таблицы переходов и диаграммы переходов. В таблице переходов строки соответственно внутренние состояниям qi считывающего устройства, столбец символом внешнего алфавита. В клетках таблицы правые части соответствующих команд. Например: Пусть А={0 1 a b c} c –вспомогательный символ q10P(a,b)|- q001n0, P(a,b)-слово длины n q10 -> q5R q20 -> q31L q4a -> 0L q21 -> R q31 -> L q4b -> 0L q2a -> R q3a -> L q4c -> 0L q2b -> R q3b -> L q50 -> q3L q3 -> q0 q3c -> q5R q51 -> q4L q40 -> R q41 -> q0L q5a -> q2R q5b -> R
|
