Элементами. Из определения следует, что элементы множества обладают двумя свойствами 1 вполне различимы 2
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Перестановка. Пусть n ϵ N0, B = {b1,b2,…,bn}. Перестановкой из элементов множества B называется всякое размещение этого множества по n элементов. Очевидно, что количество всевозможных перестановок множества B не зависит от природы элементов множества В. Поэтому количество перестановок произвольного n-элементного множества обозначим через Pn. Теорема 1: Pn = n! Доказательство: Согласно определению перестановки Pn=Ann =n*(n-1)*…*1=n!. Сочетание. Пусть n, kϵN0, knиB = {b1,b2,…,bn} - - n-элементное множество. Всякое k-элементное подмножество В называется сочетанием из n элементов этого множества по k элементов. Совершенно очевидно, что количество всевозможных сочетаний по k элементов множества В не зависит от природы элементов множества В. В силу этого, количество всевозможных сочетаний произвольного n-элементного множества по kэлементов обозначим через Сnk.
Теорема 1: Число всех k-элементных подмножеств множества из n элементов Свойства сочетаний: 1. Сn0 = 1. 2. Сnk = Сnn - k. 3. Сnk = Сn - 1k - 1 + Сn - 1k 4. Сn0 + Сn1 + Сn2 + ... + Сnn - 1 + Сnn = 2n. Бином Ньютона. Бином Ньютона - это отношение, позволяющее представить выражение (a + b)n (n ∈ Z+) в виде многочлена. Теорема 1: Имеет место равенство (a + b)n = an + Сn1an - 1b + Сn2an - 2b2 + ... + Сnkan - kbk + ... + Сnn - 1abn - 1 + bn. (1) Формулу (1) можно записать в виде (a + b)n = nk=0Cnkan-kbk. Числа Сn1, Сn2, ... , Сnn - 1 называются биномиальными коэффициентами. С помощью следующей таблицы можно определить значения биномиальных коэффициентов для любой степени. Строится он следующим образом - любое число образуется суммой рядом стоящих чисел над ним. Именно потому эта таблица имеет название треугольник Паскаля. 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 7 1 7 21 35 35 21 7 1 8 1 8 28 56 70 56 28 8 1 Слева указана степень n, справа значения соответствующих биномиальных коэффициентов. №24 r- выборки из n - множества. Определение1. Набор элементов  , ,  ,…, ,…,  из множества из множества  называется выборкой объема r из n элементов (или, иначе, называется выборкой объема r из n элементов (или, иначе,  -выборкой). -выборкой).Выборка называется упорядоченной, если порядок следования элементов в ней задан. Замечание. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными. Если порядок следования элементов не является существенным, то выборка называется неупорядоченной. В выборках могут допускаться или не допускаться повторения элементов. Определение2.Упорядоченная  -выборка, в которой элементы могут повторяться, называется -выборка, в которой элементы могут повторяться, называется  -размещением с повторениями. -размещением с повторениями.Определение3.Упорядоченная  -выборка, элементы которой попарно различны, называется -выборка, элементы которой попарно различны, называется 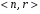 -размещением без повторений (или, иначе, -размещением без повторений (или, иначе,  -размещением). -размещением).Замечание.  -размещения без повторений называются перестановками множества X. -размещения без повторений называются перестановками множества X.Определение4.Неупорядоченная  -выборка, в которой элементы могут повторяться, называется -выборка, в которой элементы могут повторяться, называется  -сочетанием с повторениями. -сочетанием с повторениями.Определение5.Неупорядоченная  -выборка элементы, которой попарно различны, называется -выборка элементы, которой попарно различны, называется  -сочетанием без повторений (или, иначе, -сочетанием без повторений (или, иначе,  -сочетанием). -сочетанием).Замечание. Любое  -сочетание можно рассматривать, как r-элементное подмножество n-элементного множества. -сочетание можно рассматривать, как r-элементное подмножество n-элементного множества.Число 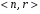 -размещений с повторениями будем обозначать -размещений с повторениями будем обозначать 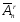 , а без повторений – через , а без повторений – через  . Число перестановок n-элементного множества будем обозначать через . Число перестановок n-элементного множества будем обозначать через  (т.е. (т.е.  ). Число ). Число  -сочетаний с повторениями будем обозначать через -сочетаний с повторениями будем обозначать через  , а без повторений – через , а без повторений – через  . .25. Перестановки с повторениями Пусть задано конечное множество U={a1,a2,…,an}. Рассмотрим набор из элементов ai1,ai2,…,aik где ai  U, i U, i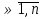 , k≤n этот набор называется выборкой объемов к из n элементов. , k≤n этот набор называется выборкой объемов к из n элементов.Выборка называется упорядоченной, если в ней задан порядок следование элементов, если порядка следования не существует, то выборка называется неупорядоченной. Упорядоченные выборки n из n называется перестановкой. Число таких перестановок Pn=n! Упорядочен выборки объем m из n элементов(m 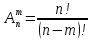 . .Перестановка с повторениями : пусть имеется n элементов среди которых , к1 элементов 1 типа , к2 элементов 2 типа … кr элемент r типа. Причем к1+к2+…+ кr=n упорядочен выборки из таких m элементов по n называется перестановкой с повторением и обозначается  (k1,k2,…,kr) = (k1,k2,…,kr) = , их называют полиниальными коэффициентами. , их называют полиниальными коэффициентами.26. Полиномиальная теорема. Принцип Дирихле. Принцип Дирихле : Если в m ящиках расположены n кроликов, при этом (n>m) то хотя бы в 1 из ящиков будет находиться больше чем 1 кролик . (Например :9 ящиков , 10 кроликов.) Если n кроликов рассажены в m ящиках, то хотя бы в 1 ящике находится не менее  кроликов, а также хотя бы в 1 ящике не более кроликов, а также хотя бы в 1 ящике не более  кроликов. кроликов.Полиномиальная теорема: Выражение  равно сумме всех возможных слагаемых вида равно сумме всех возможных слагаемых вида  , где r1+r2+…+ , где r1+r2+…+ =n, то =n, то есть  = = . .Доказательство: Перемножим последовательность  n раз. Тогда получаем n раз. Тогда получаем  слагаемых вида d1…dn, где каждый множитель di равен или а1, или а2 ,…, или  .Обозначим .Обозначим через В(r1,…,  ) совокупность всех слагаемых , ) совокупность всех слагаемых , где а1 встречается множителем r1 раз ,а2-r2 раз , …,  - - раз .Число таких слагаемых равно раз .Число таких слагаемых равно Cn( r1,…,  ). Но Cn( r1,…, ). Но Cn( r1,…, )= )=  . .Следовательно  = = . .27.Рекуррентные соотношения и производящие функции. Рекуррентные соотношения :это соответствия позволяющие свести решение комбинаторной задачи для некоторого числа объектов к аналогичной задаче с меньшей размерностью. Пусть f(n) некоторое рекуррентное соотношение и для него известно  =F( =F( )(1). Где F(y1,…,yk) известная функция от k переменных тогда (1) называется рекуррентным соотношением к –ого порядка. Последовательность чисел )(1). Где F(y1,…,yk) известная функция от k переменных тогда (1) называется рекуррентным соотношением к –ого порядка. Последовательность чисел  называется решением соотношения (1), если при подстановке называется решением соотношения (1), если при подстановке 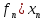 в (1) получается верное равенство. в (1) получается верное равенство.Если в (1) первые к соотношений f1,f2,…fk заданы произвольно то соотношение (1) имеет бесконечное число соотношений. Опр: Пусть f(n) общее решение соотношения (1) если оно зависит от к произвольных постоянных то записывают  = = (С1,С2…Сn,n). Если для любого Xn существует С1’,С2’…Ск’ что (С1,С2…Сn,n). Если для любого Xn существует С1’,С2’…Ск’ что  является решением то записывают Xn= является решением то записывают Xn= (С1’,С2’…Ск’,n). (С1’,С2’…Ск’,n). Опр: Линейное однородное рекуррентное соотношение 2-го порядка с постоянными коэффициентами называется рекуррентным соотношением вида  = = ,n=1,2…(2) ,n=1,2…(2)Уравнение 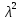 =а1 =а1 +а2 (3) называется характеристическим уравнением соотношения (2). +а2 (3) называется характеристическим уравнением соотношения (2).Теор: Если характеристическое уравнение (3) имеет 2 различных корня  2 то общее решение рекуррентного соотношения (2) имеет вид, 2 то общее решение рекуррентного соотношения (2) имеет вид,  =С =С +С2 +С2 . Если уравнение (3) имеет кратные корни то общее решение имеет вид . Если уравнение (3) имеет кратные корни то общее решение имеет вид  =(С1+С2) =(С1+С2) . .Опр: Линейное рекуррентное соотношение к-го порядка называется соотношение вида  =а1 =а1 +а2 +а2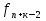 +…+ +…+  + +  (4). (4).Характеристическим для (4) будет уравнение вида  =а1 =а1 +а2 +а2 +…+ +…+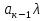 + + .(5) .(5) Теор: 1)Пусть  ,…, ,…, Попарно различные корни характеристического уравнения (5) Тогда общее уравнение (4) записывается в виде Попарно различные корни характеристического уравнения (5) Тогда общее уравнение (4) записывается в виде  =С =С +С2 +С2 …+ Сn …+ Сn 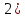 Пусть Пусть  ,…, ,…, попарно различны корни характеристического уравнения (5) имеющие кратность mi причем m1+m2+…+mp=k, i=1,p. Тогда общее решение уравнения (4) имеет вид попарно различны корни характеристического уравнения (5) имеющие кратность mi причем m1+m2+…+mp=k, i=1,p. Тогда общее решение уравнения (4) имеет вид  =(С11+С12n+…+ =(С11+С12n+…+ ) ) +…+(Cp1+Cp2+… +…+(Cp1+Cp2+… ) ) . Для решения рекуррентных соотношений используют так же метод производящих функций. . Для решения рекуррентных соотношений используют так же метод производящих функций. Пусть задано линейное рекуррентное соотношение а0=0, а1=1, аn=5  , n>=2. , n>=2. Производящую функцию G(z)будем искать в виде ряда  =a0+a1z+a2 =a0+a1z+a2 +… с этой целью отношение G умножают соответственно на +… с этой целью отношение G умножают соответственно на  …. 0 …. 0 +1 +1 +…+(5 +…+(5 ) ) +…+a0+a1z+ +…+a0+a1z+ =z+5 =z+5 -6 -6 G(z)=z+5zG(z)-6 G(z)=z+5zG(z)-6 G(z). Откуда производящая функция G(z)= G(z). Откуда производящая функция G(z)= . Оно задает производящую функцию последовательности (5) в замкнутом виде . Оно задает производящую функцию последовательности (5) в замкнутом виде  = = + +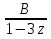 . An= . An= - - ,n=0,1,2… решение рекурсивного выражения 5. ,n=0,1,2… решение рекурсивного выражения 5.28. Принцип включения и исключения: Теорема. Если А1, A2, ..., An – некоторые конечные множества, то: m(A1 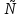 A2 A2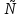 … …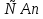 )=[m(A1)+…+m(An)]-[m(A1 )=[m(A1)+…+m(An)]-[m(A1 )+m(A1 )+m(A1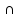 A3)+…+m(An-1 A3)+…+m(An-1 )]+[m(A1 )]+[m(A1 )+…+m(An-2 )+…+m(An-2 )]-…+( )]-…+( [m(A1 [m(A1 )]. )].Поясним формулировку этой теоремы. Правая часть формулы в теореме представляет собой алгебраическую сумму n слагаемых (взятых в квадратные скобки), имеющих попеременно знак «+» и «–».Первое слагаемое – число элементов, входящих хотя бы в одно из множеств А1, A2, ..., An, второе – число элементов, входящих хотя бы в одно из множеств  (i < j, i = 1, …, n, j = 1, …, n), третье – число элементов, входящих хотя бы в одно из множеств (i < j, i = 1, …, n, j = 1, …, n), третье – число элементов, входящих хотя бы в одно из множеств  (i < j < k, i = 1, …, n, j = 1, …, n, k = 1, …, n) и так далее. . Последнее слагаемое, взятое со знаком (i < j < k, i = 1, …, n, j = 1, …, n, k = 1, …, n) и так далее. . Последнее слагаемое, взятое со знаком  , – число элементов в множестве A1 , – число элементов в множестве A1 . Такое попеременное включение и исключение слагаемых с целью учета каждого элемента только один раз и послужило причиной для названия этой формулы: формула включений и исключений. . Такое попеременное включение и исключение слагаемых с целью учета каждого элемента только один раз и послужило причиной для названия этой формулы: формула включений и исключений.Эту формулу можно доказать, используя метод математической индукции. Мы ограничимся ее доказательством только для случая n = 3, то есть покажем, что m(AUBUC)= m(A)+m(B)+m(C)-m(B  )-m(A )-m(A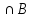 )-m(A )-m(A )+m(A )+m(A ) )Доказательство. Чтобы не писать индексы, рассмотрим множества А, В, С. Используя очевидное равенство AU B UC = AU(B UC) и то, что эта формула доказана для двух множеств, получим: m(AU B UC) = m(AU[B UC]) = m(A) + m(B UC) − m(A  [B UC]) , [B UC]) , |
