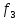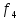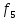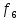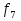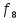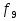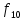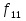Элементами. Из определения следует, что элементы множества обладают двумя свойствами 1 вполне различимы 2
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
Булева алгебра. Булевой алгеброй называется непустое множество A с двумя бинарными операциями  (аналог конъюнкции), (аналог конъюнкции), (аналог дизъюнкции),унарной операцией (аналог дизъюнкции),унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы: (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:7. Булевы функции. Мощность множества булевых функций от 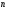 переменных. переменных.Функции, определенные на множестве E2={0,1} и принимающее значение на множестве называются булевыми функциями или функция алгебры логики. Функцию F алгебры логики удобно задавать при помощи таблицы, в которой аргументы расположены в порядке возрастания, т.е. будем считать что аргументы упорядочены в алфавитном порядке, т.е. будем обозначать, что аргумент(0,0,0,1) предшествует({) аргументу (0,0,1,0), а аргумент (0,0,1,0){(1,0,0,1). Наборы 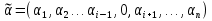 , , 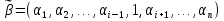 будем называть соседними по i-й координате, а наборы будем называть соседними по i-й координате, а наборы 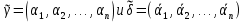 называются противоположными. называются противоположными.Символом 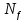 будем обозначать количество наборов переменных, при которых функция принимает значение 1. будем обозначать количество наборов переменных, при которых функция принимает значение 1.Свойства булевой функции:
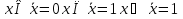 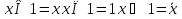 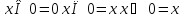 Совокупность всех булевых функций относительно операций логического умножения, сложения, отрицания является алгеброй булевой функций. Соотношение между булевой алгеброй и алгеброй Кантора и есть изоморфизм, т.к. любая алгебра обладающая свойствами 1-10 называется булевой алгеброй. Функцию f, определенную на множестве всех n-мерных векторов 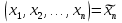 , где числа , где числа 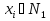 , будем называть булевой функцией от n переменных и будем записывать в виде , будем называть булевой функцией от n переменных и будем записывать в виде 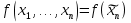 . .Мощность множества всех булевых функций от n переменных для фиксированного n- это количество булевых функций от n переменных. Мощность высчитывается по формуле 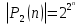 8.Элементарные булевы функции. Будем рассматривать следующие элементарные функции:
Таблица истинности для функции с одной переменной.
Таблица истинности для функций с 2 переменными
9. Формулы. Основные эквивалентности формул. В каждой формуле 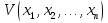 над полем Р сопоставляется функция над полем Р сопоставляется функция 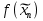 из Р2 множество всех возможных булевых функций. из Р2 множество всех возможных булевых функций.Формулы V и G считаются эквивалентными, если соответствующие им функции fu = hg равны. Правила: 1. Внешние скобки в формулах как правило опускаются. 2. Формула U 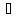 G записывается в виде U●G или UG. G записывается в виде U●G или UG.При этом считают, что знак отрицания связывает сильнее, чем логическое 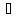 знак умножить связывает сильнее, чем знак любой из операций или знак умножить связывает сильнее, чем знак любой из операций или 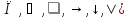 А знак = связывает слабее, чем вышеперечисление операции в формуле. Функции f1 – f11 – Элементарные функции подчиняются следующим эквивалентности:
xy = 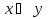 = x⊕y⊕1 = x⊕y⊕1 xy = ( 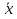 ∨y)&(x∨ ∨y)&(x∨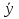 ) = x&y ∨ ) = x&y ∨ 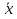 & &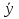
x ⊕ y = (x& 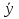 ) ∨ ( ) ∨ (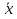 & y) = ( & y) = (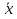 ∨ ∨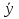 ) & (x ∨ y) ) & (x ∨ y)
x→y = 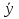 → →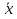 x→y = xy⊕x⊕1 x→y = xy⊕x⊕1 x→ 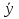 = y→ = y→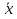 x→y = x→y = 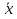 ∨y x→y= ∨y x→y= 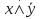 Порядок действий в формулах алгебры логики Если в выражениях нет скобок, то очередность выполнения логических операций следующая: 1) отрицание; 2) конъюнкция; 3) дизъюнкция; 4) логическое следование; 5) сумма по модулю 2 и эквивалентность. Из тождеств 1-10 вытекают правила:
Совокупность всех булевых функций относительно операций логического умножения, сложения, отрицания является алгеброй булевых функций. Соотношение между булевой алгеброй и алгеброй Кантора и есть изоморфизм, т.к. любая алгебра обладающая свойствами 1-10 называется булевой алгеброй. 10. Принцип двойственности. Двойственные булевы функции. Функция 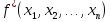 называется двойственной к функции называется двойственной к функции 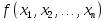 если имеет место равенство: если имеет место равенство: 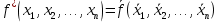 , и если f*=f, то такая функция называется самодвойственной на множестве всех самодвойственных функций, которые обозначаются S. , и если f*=f, то такая функция называется самодвойственной на множестве всех самодвойственных функций, которые обозначаются S.Принцип двойственности:  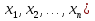 может быть записана в виде: может быть записана в виде: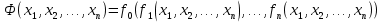 , при чем , при чем 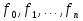 имеют двойственные функции имеют двойственные функции 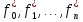 , то , то 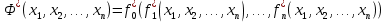 . .Лемма о несамодвойственности: Если функция 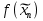 несамадвойственна, то из нее путем подстановки переменных, х, несамадвойственна, то из нее путем подстановки переменных, х, 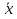 на места ее переменных можно получить константу. на места ее переменных можно получить константу.11.Теорема о разложении Теорема о разложении булевых функций по переменным. Каждую функцию алгебры логики f(x1, x2, …, xn) для ∀m ∈ {1, 2, …, n} можно представить в виде 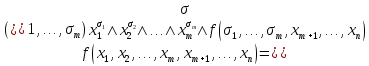 , где дизъюнкция берется по всевозможным наборам значений переменных x1,…, xm. Такое представление функции f называется разложением этой функции по m переменным. , где дизъюнкция берется по всевозможным наборам значений переменных x1,…, xm. Такое представление функции f называется разложением этой функции по m переменным. Доказательство: Рассмотрим произвольный набор значений переменных (α1,…,αn), и вычислим f(α1, …, αn) сначала стандартным образом, а затем как в формулировке доказываемой теоремы: 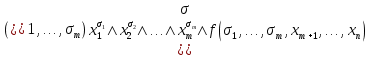 =[по ранее доказанному, если =[по ранее доказанному, если 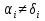 , то , то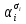 ]=, ]=, 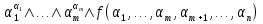 =[так что =[так что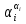 =1]=f(α1, …, αn), что и требовалось доказать. =1]=f(α1, …, αn), что и требовалось доказать. Следствия: 1) Если m=1, то f(x1,…,xn)= 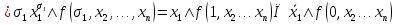 2) m=n. Тогда f(x1, …, xn)= 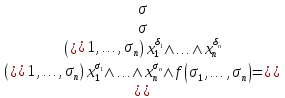 , так как остались лишь те наборы, при которых , так как остались лишь те наборы, при которых 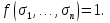 Получаем из следствия 2 равенство: f(x1,…,xn)= 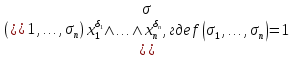 12. Совершенные дизъюнктивные нормальные формы. Совершенная дизъюнктивная нормальная форма принимает такой вид f(x1,…,xn)= 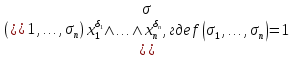 , которое следует из второго следствия теоремы о разложении. , которое следует из второго следствия теоремы о разложении.Такая форма является единственной для каждой булевой функции, кроме 0. Каждое из выражений вида 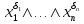 называется элементарной конъюнкцией. называется элементарной конъюнкцией.Замечание. СДНФ называется совершенной, потому что каждое слагаемое в дизъюнкции (т.е. элементарная конъюнкция) содержит все переменные; дизъюнктивной, потому что главная операция – дизъюнкция; нормальной, поскольку совершенный вид такой формы является однозначным (с точностью до порядка записи элементарных конъюнкций) способом записи формулы, реализующей заданную функцию. Пример. Функция f равна 1 на наборах (0,0,1), (0,1,0) и (1,0,1), поэтому СДНФ 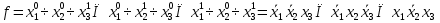 СДНФ: 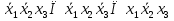 №13 Совершенные конъюнктивные нормальные формы Элементарной конъюкцией (ЭК) наз. формула: 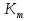 = =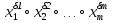 , где , где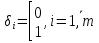 , а , а 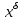 = =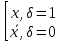 . Тогда формула вида: . Тогда формула вида: 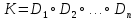 наз. конъюктивной норм.формой (КНФ). наз. конъюктивной норм.формой (КНФ).КНФ над множ. переменных 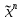 =( =(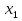 , , 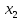 , … , , … , 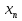 )наз. совершенной если она составлена из попарно различных ЭК. При этом m – входящее в состав ЭК назыв. рангом. Например: Из )наз. совершенной если она составлена из попарно различных ЭК. При этом m – входящее в состав ЭК назыв. рангом. Например: Из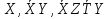 – ЭК, – ЭК, 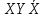 –не явл. ЭК. –не явл. ЭК.Теорема: любая булева функ. 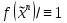 может быть представлена в виде соверш. КНФ: может быть представлена в виде соверш. КНФ: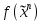 = Ʌ ( = Ʌ (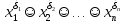 ),⍱( ),⍱(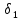 , … , , … , 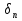 ), при чем f( ), при чем f(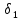 , … , , … , 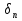 )=0, такое представление единственно. )=0, такое представление единственно.Пример: представить ф-цию в виде соверш КНФ: f( 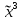 )=( )=(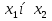 )→ )→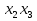  K=( 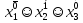 )Ʌ( )Ʌ(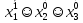 )Ʌ( )Ʌ(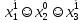 )=( )=(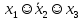 )Ʌ( )Ʌ(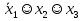 )Ʌ( )Ʌ(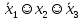 ) )№ 14 Существенные и фиктивные переменные. Будем говорить, что f( 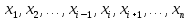 )существенным образом зависит от переменной, )существенным образом зависит от переменной,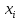 если найдётся такой набор если найдётся такой набор 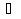 =( =(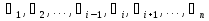 ) что f( ) что f(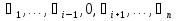 )≠f( )≠f(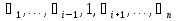 ) не совпадают. ) не совпадают.В противном случае переменная 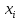 наз. несущественной или фиктивной. наз. несущественной или фиктивной.Функции f( 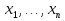 ) и g( ) и g(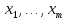 ) считаются равными, если функцию g можно получить из f путём добавления (вычёркивания) фиктивных переменных. ) считаются равными, если функцию g можно получить из f путём добавления (вычёркивания) фиктивных переменных.Для функции f получить существенные и фиктивные переменные.  f(0,0,0)=0 f(1,0,0)=1 0≠1 Переменная x – существенная ⍱( 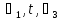 ), f( ), f(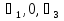 )=f( )=f(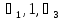 ) )y – фиктивная, z – фиктивная. Если 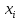 – существенная переменная ф-цииf( – существенная переменная ф-цииf(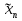 ), то в разложении этой ф-ции по i-ой переменной кортежи значений ), то в разложении этой ф-ции по i-ой переменной кортежи значений 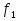 ( (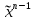 ), ), 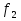 ( (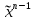 ) соответствующие ) соответствующие 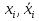 будут различные. будут различные.В случае если 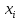 – фиктивная переменная, одинаковыми. – фиктивная переменная, одинаковыми.Переменная 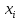 явл. существенной для функции f явл. существенной для функции f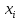 явно входит в полином Жегалкина. явно входит в полином Жегалкина.Пусть 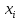 – существенная переменная функ. f, но она не входит в явном виде в полином Жегалкина. – существенная переменная функ. f, но она не входит в явном виде в полином Жегалкина.Т.к. представл. любой ф-ции в виде полинома Жегалкина единственно, то такое предложение неверно. Пусть 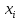 явно входит в полином Жегалкина, тогда его можно записать в виде f = явно входит в полином Жегалкина, тогда его можно записать в виде f =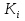 *Q( *Q( )⊕R( )⊕R( ), где QиR–полиномы не содержащие ), где QиR–полиномы не содержащие 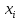 , причём Q≠0. , причём Q≠0.Пусть ( 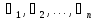 ) такой набор, что Q( ) такой набор, что Q(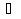 )=1.Тогдаf( )=1.Тогдаf(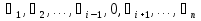 )=0*Q(⍺)+R(⍺)=0*1+ R(⍺)=R(⍺) )=0*Q(⍺)+R(⍺)=0*1+ R(⍺)=R(⍺)f( 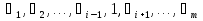 )=1*Q(⍺)+R(⍺)= )=1*Q(⍺)+R(⍺)=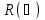 . .Если функция f( 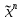 ) представима в виде полинома Жегалкина степени не меньше 2, то она содержит не менее двух существенных переменных. ) представима в виде полинома Жегалкина степени не меньше 2, то она содержит не менее двух существенных переменных.№15 Полином Жегалкина. Теорема: Каждая ф-ция f( 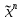 ) может быть выражена в виде формулы через конъюкцию, дизъюнкцию и отрицание (˄, ˅, ┐). ) может быть выражена в виде формулы через конъюкцию, дизъюнкцию и отрицание (˄, ˅, ┐).Выражение над множеством переменных 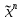 вида: вида: 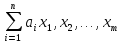 , где , где 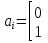 а суммирование ведётся по модулю 2 наз. полиномом Жегалкина. При этом 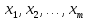 –все возможные произведения составл. из переменных –все возможные произведения составл. из переменных 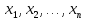 . .Например полином Жегалкина для функции двух переменных имеет вид:f( 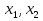 )= )=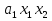 ⊕ ⊕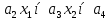 Ранг наибольшей из элементарных конъюнкций (ЭК) входящих в полином Жегалкина наз. степенью этого многочлена. №16 Представление булевой функции в виде полинома Жегалкина. Теорема:Каждая функция алгебры логики может быть представлена в виде полинома Жегалкина и это представление единственно. Произвольную функ. f( 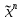 ) можно задать в виде полинома Жегалкина методом неопределённых коэффициентов. ) можно задать в виде полинома Жегалкина методом неопределённых коэффициентов.Пример: Найти полином Жегалкина для функции f( 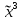 )=( )=(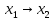 )*( )*(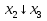 ) ) f( 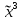 )= )=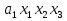 ⊕ ⊕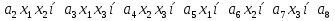 f(0,0,0)= 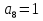 f(0,0,1)= 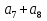 = , = ,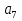 =1 =1f(0,1,0)= 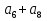 =0 , =0 ,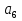 =1 =1f(0,1,1)= 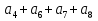 =0 , =0 , 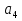 =1 =1f(1,0,0)= 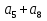 =0 , =0 , 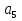 =1 =1f(1,0,1)= 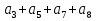 =0 , =0 , 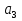 =1 =1f(1,1,0)=0 , 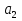 =1 =1f(1,1,1)=0 , 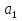 =1 =1f( 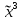 )= )=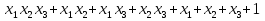 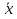 =x =x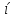 1 1f= 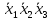 =( =(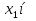 1)( 1)(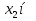 1)( 1)(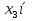 1)=( 1)=(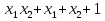 )( )(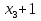 )= )=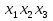 + +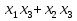 + +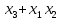 + +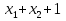 С помощью эквивалентных преобразований получить полином Жегалкина для функции:f=(x˅y 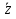 )(x˅z) )(x˅z)x˅y= 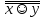 = =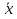 ˄ ˄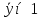 =(x+1)(y+1)+1=xy+x+y+1+1 =(x+1)(y+1)+1=xy+x+y+1+1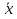 =x =x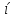 1 1f=(x˅y 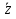 )(x˅z)=(xy )(x˅z)=(xy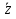 +x+y +x+y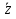 )(xz+x+z)=xy )(xz+x+z)=xy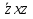 +xxz+ +xxz+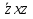 +xy +xy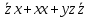 + +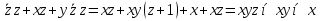 x˅y=xy 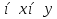 f=(x˅y 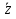 )(x˅z)=x )(x˅z)=x№17 Замкнутый класс T0. Говорят, что функция f( 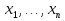 ) сохраняет константу 0 , если значение функции f(0,0, … ,0)=0 ) сохраняет константу 0 , если значение функции f(0,0, … ,0)=0Множество всех таких функций обозначается 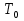 . .1)Пример: f( 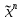 )=(0110 1001 1010 0101) )=(0110 1001 1010 0101)fͼ 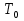  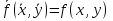 2)Пример, линейных функций содержащихся только в 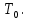 f( 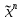 )= )=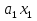 + +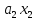 + … + + … +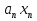 + +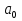 чтобы fͼ 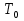  №18 Замкнутый класс T1. Говорят, что функция f( 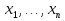 ) сохраняет константу 1 , если значение функции f(1,1, … ,1)=1 ) сохраняет константу 1 , если значение функции f(1,1, … ,1)=1Множество всех таких функций обозначается 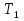 . .1)Пример: f( 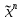 )=(0110 1001 1010 0101) )=(0110 1001 1010 0101)fͼ 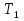  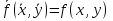 2)Пример, линейных функций содержащихся только в 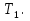 f( 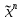 )= )=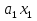 + +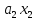 + … + + … +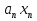 + +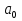 чтобы fͼ 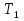 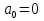 , n=2k+1 , n=2k+1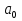 ≠0, n=2k ≠0, n=2k№19 Замкнутый класс S. Функцияf*(x1,x2,…,xn) называется двойственной к функции f(x1,x2,…,xn) если имеет место равенство:f*(x1,x2,…,xn)=f̅(x̅1,x̅2,…,x̅n) Если f*= f, то такая функция называется самодвойственной. Множество всех самодвойственных функций обозначается S Принцип двойственности: Если формула в видеF(x1,…,xn) может быть записана в видеF(x1,…,xn)=f0(f1 (x1,…,xn), f2 (x1,…,xn),…, fn(x1,…,xn)) причемf0,f1 , f2 ,…,fnимеют двойственные функцииf0*,f1*, f2*,…,fn* , тоF*(x1,…,xn)= f0*(,f1*, f2*,…,fn*) Лемма( о несамодвойственности): Если функция f(x̃n) несамодвоиственная (S), то из нее путем подстановки переменных x,x̅ на места ее переменных можно получить константу. №20 Замкнутый класс L. Функция f(x̃n) называется линейной если ее представление в виде полинома Жегалкина имеет вид f(x̃n)=a0+a1x1+…+anxn , aiϵ{0,n}, множество всех линейных функций обозначается через L. Лемма (о нелинейности):Если функция f(x̃n)линейна, то из нее путем подстановки на места ее переменных констант 0,1 и переменных x,x̅, а также быть может навешиванием отрицания над всей функцией f можно получить конъюнкцию x1Ʌx2 №21 Замкнутый класс M. Наборы α̃=(α1,…,αn) иβ̃=(β1,…,βn)говорят что для них выполнено отношение предшествованияα̃{β̃ еслиα1≤β1,…, αn≤βn Функция f(x̃n) монотонной если α̃,β̃ удовлетворяющие условиюα̃{β̃ =>f(α)≤f(β) Множество всех монотонных функций обозначается M. Лемма (о немонотонности ): Если функцияf()М то из нее путем подстановки на места ее переменных констант 0,1 и переменной x можно получить функцию x̅. №22 Теорема Поста о полноте со следствием. Теорема 1(Поста критерий полноты): Система функций {f1,f2,f3,…}(1) fiϵB2полна тогда и только тогда, если она не содержится целиком ни в одном из классовT0, T1, M, L, S. Другими словами: система (1) полна тогда и только тогда, когдаf1T0, f2 T1, f3 M, f4 L, f5 S,причем среди функций не все функции обязательно различные. Теорема 2: Пусть заданы системы функций. Если система функций (2) функционально полна, а функции системы (3) выражаются через функции системы (2), то система (3) также функционально полна. Система функций G называется независимой если никакая функция f этой системы не выражается через остальные, т.е. для любой fϵG будет выполнено условие fG̅/̅f̅. Независимая система функций G называется базисом замкнутого класса K, если всякая функция FϵK есть суперпозиция функций системы G. Следствие 1(из теоремы Поста): всякий замкнутый класс QP2 содержится целиком хотя бы в одном из классовT0, T1, M, L, S. Иначе он бы представлял собой полную систему и в силу замкнутости равнялся P2. P2-слет. всех возможных булевых функций. Следствие 2: Если к какому либо из классов (S T0, T1, M, L) добавить любую функцию, не принадлежащую этому классу, то система Su{f} является функционально полной, а ее замыкание совпадает с P2. Поэтому классы T0, T1, M, L, S называются предполными. Следствие 3: в P2 существует только пять предполных классов T0, T1, M, L, S. Другие классы предполными не являются. Следствие 4: Из теоремы Поста и следствий 1-3 следует что если в системе присутствуют константы 0 и 1, то для полноты системы, достаточно чтобы в ней содержалась немонотонная функция и нелинейная функция. №23 Сочетания и перестановки. Бином Ньютона. |

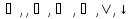
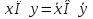
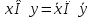 правило де моргана
правило де моргана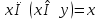
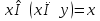 правило поглощения
правило поглощения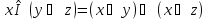
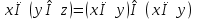
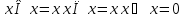
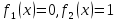 наз. Тождественный нуль и тождественная единица.
наз. Тождественный нуль и тождественная единица.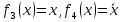 наз. Тождественная функция истинности и отрицание
наз. Тождественная функция истинности и отрицание 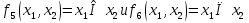 конъюнкция
конъюнкция 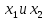 и дизъюнкция
и дизъюнкция 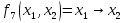 импликация
импликация 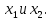
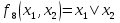 функция Шеффера (отр. конъюнкция
функция Шеффера (отр. конъюнкция 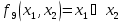 эквивалентности
эквивалентности 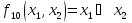 сумма по модулю 2 (отр. Эквивалентности
сумма по модулю 2 (отр. Эквивалентности 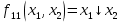 стрелка Пирса, (отр. дизъюнкция
стрелка Пирса, (отр. дизъюнкция