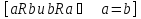Элементами. Из определения следует, что элементы множества обладают двумя свойствами 1 вполне различимы 2
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
1. Под множеством понимают совокупность определенных, вполне различных объектов, рассматриваемых как единое целое. Объекты из которых состоит множество называются элементами. Из определения следует, что элементы множества обладают двумя свойствами: 1) вполне различимы; 2) все имеют общее свойство Множество обозначаем :A, B, …,X, Y, Z, их элементы: a, b, …, x, y, z. 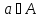 – отношение принадлежности элемента a к мн-вуA. – отношение принадлежности элемента a к мн-вуA.a 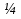 A - отношение непринадлежности элемента a к мн-вуA. A - отношение непринадлежности элемента a к мн-вуA.Множество B называется подмножествомA , если каждый элемент множества B принадлежит множеству A (B≤A) Множества A и Bназываются равными если они состоят из одних и тех же символов (A=B), если B≤A, B≠A, то B  A, в этом случае B-собственное подмножество мн-ваA. A, в этом случае B-собственное подмножество мн-ваA.Не всякая совокупность объектов является множеством. Мн-во не содержащее ни одного элемента наз. пустым (ø).ø≤A,  А АМножество состоящее из конечного числа элементов 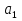 , , 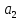 , …, , …, 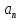 называется конечным. В противном случае бесконечным. называется конечным. В противном случае бесконечным.Количество элементов конечного множества называется мощностью этого множества (n=|A|) A={ 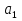 , , 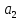 , …, , …, 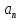 } }Мн-ва, равномощные мн-ву натуральных чисел наз. счетными (Ν) Равномощные мн-ва действительных чисел континуальные (R) Все рассматриваемые мн-ваA,B,C,…,N,RU и наз. универсальными. Имеют место два принципа, которые играют роль аксиом: 1) принцип объемности: множества A и B наз. равными если они состоят из одних и тех же элементов. Формой от x будем называть конечную последовательность состоящую из слов и символа x такую что если каждое вхождение x в эту последовательность заменить одним и тем же именем , то в результате получим истинное (ложное) высказывание. 2) принцип абстракции. Любая форма P(x) определяет некоторое множество A, а именно только тех элементов множества А для которых aϵA, P(a) – истинное высказывание. В этом случае мн-во А можно задавать в виде A={x|P(x)}; A={x:P(x)} P(x) наз. также характерным св-вом или распознающей процедурой. Способы задания множеств: 1) перечисление A={ 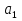 , , 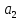 , …, , …, 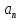 }; |A|=3; 2) описание характеристических свойств B={x|x=2n, nϵN}; 3) при помощи порождающей процедуры (т.е. алгоритма). Позволяет получать элементы мн-ва из уже имеющихся элементов, либо других объектов, в этом случае мн-во C содержит все объекты, которые можно получить при помощи этой процедуры }; |A|=3; 2) описание характеристических свойств B={x|x=2n, nϵN}; 3) при помощи порождающей процедуры (т.е. алгоритма). Позволяет получать элементы мн-ва из уже имеющихся элементов, либо других объектов, в этом случае мн-во C содержит все объекты, которые можно получить при помощи этой процедуры Основные операции над множествами:1. Объединением (A 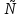 B) множеств A и B наз. множество A B) множеств A и B наз. множество A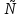 B, состоящее из всех элементов, которые принадлежат хотя бы одному из множеств A или B. A B, состоящее из всех элементов, которые принадлежат хотя бы одному из множеств A или B. A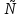 B= {x| xϵA или xϵB }. 2. Пересечение. Пересечением множеств A B= {x| xϵA или xϵB }. 2. Пересечение. Пересечением множеств A B называют множества A и B состоящее из тех и только тех элементов, которые принадлежат и множеству A и множеству B. A B называют множества A и B состоящее из тех и только тех элементов, которые принадлежат и множеству A и множеству B. A B= {x| xϵA и xϵB}; A B= {x| xϵA и xϵB}; A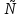 B B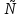 … …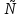 C; T C; T M M … …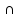 N. 3 Разностью мн-в A и B наз. мн-во A\Bсостоящее из всех элементов мн-ваA N. 3 Разностью мн-в A и B наз. мн-во A\Bсостоящее из всех элементов мн-ваA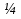 мн-вуB. A\B={x| xϵA и x неϵB }; A\B мн-вуB. A\B={x| xϵA и x неϵB }; A\B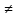 B\A. Операция всегда двуместная и некоммутативная. 4) Дополнение до универсального мн-ва U.(Ā) которое состоит из всех элементов мн-ва U не содержащихся в A. Ā=U\A=={x| xϵU и xнеϵA }. Операции объединения, пресечения и дополнения называют булевы операции над множествами. B\A. Операция всегда двуместная и некоммутативная. 4) Дополнение до универсального мн-ва U.(Ā) которое состоит из всех элементов мн-ва U не содержащихся в A. Ā=U\A=={x| xϵU и xнеϵA }. Операции объединения, пресечения и дополнения называют булевы операции над множествами.Свойства операций:1 Коммутативность : 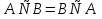 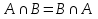 2 Ассоциативность : 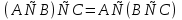 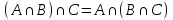 3 Идемпотентность: 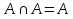 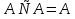 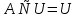 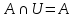 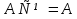 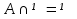 4 Дистрибутивность: 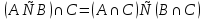 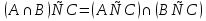 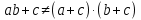 5 Законы де Моргана (отрицание). 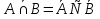 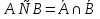 6 Инволюция (правило двойного отрицания): 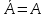 2.Высказывания.Операции над высказываниями. Высказывание-утверждение, о котором можно сказать истинно оно или ложно. Обозначается малыми (прост выск.)или большими(сложные выск.)буквами латинского алфавита. Отрицанием высказ. а наз. высказывание 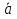 ,которое принимает значение «истиности», если а-«ложно»,и принимает значение 0,если а-1,т.е. задается след табл истинности: а-0 ,которое принимает значение «истиности», если а-«ложно»,и принимает значение 0,если а-1,т.е. задается след табл истинности: а-0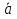 -1, а-1 -1, а-1 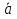 -0, -0, 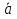 -«отрицание а,не а,не верно, что а» -«отрицание а,не а,не верно, что а»Дизъюнкцией двух высказываний называется такое новое высказывание, которое истинно тогда и только тогда, когда истинно ХОТЯ БЫ ОДНО из этих высказываний. Конъюнкцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда истинны оба высказывания А и В. Импликацией А => В называется высказывание, которое ложно тогда и только тогда, когда А истинно и В ложно. Эквиваленцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда оба эти высказывания А и В истинны или оба ложны. 3. Тождественно истинные и тождественно ложные высказывания. Равносильные высказывания. Высказывание А(а1,..аn) наз. тождественно истинное, если оно принимает значение 1 при любых наборах истинностных значений, входящих в него прост высказывание а1,..аn. Высказывание А(а1,..аn) наз. тождественно ложное, если оно принимает значение 0 при любых наборах истинностных значений, входящих в него прост высказывание а1,..аn. Высказывание А(а1,..аn)и В(а1,..аn)наз. равносильными, если истинностные значение этих высказываний на одинаковых наборах истинностных значений, входящих в них простейших высказываний а1,..аn совпадают.А(а1,..аn)≡В(а1,..аn). Прим. А(а,b)= 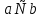 и В(а,b)= и В(а,b)=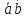 4.Суперпозиция функций. Бинарные отношения. Свойства бинарных отношений Суперпозицией ф-ции наз. ф-цию, полученную из системы ф-цийf, g1,…,gk некоторой подстановкой во внешнюю ф-цию f ф-ций g1,…,gk на месте её переменных и переименованиями переменных. Например: f(x,y,z)=3x+5y2-z; g1(x,y)=X-Y; g1(x)=lnx; h1(x,z)=3(x-z)+5(x-z)2-lnz; h2(x,z)= 3(x-z)+5ln2(x-z)-lnz; h3(x,y,z,s)= 3(x-y)+5ln (y-s)2-ln(z-s); Бинарные отношения. Свойства бинарных отношений. Пусть задано не пустое множество 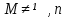 – арным (n – местным) отношением на мн-ве М наз. подмн-во – арным (n – местным) отношением на мн-ве М наз. подмн-во 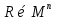 которое обозначатся R(m1,m2,…,mn), при этом говорят, что элементы (m1,m2,…,mn) (весть спектр) находится в отношении R. которое обозначатся R(m1,m2,…,mn), при этом говорят, что элементы (m1,m2,…,mn) (весть спектр) находится в отношении R.Число n наз. арностью (или местностью) отношения. Если n=1, то говорят, что задана одноместное (унарное) отношение, а одноместное наз. св-вом или признаком мн-вом М к св-вом можно отнести эти 2 случая. В случае n=2, отношение наз. бинарным. Бинарное отношение - мн-во всех пар 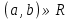 которое в общем случае которое в общем случае 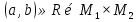 . .Отношение R 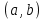 чаще записывают в виде aRb элементы a и b находятся в отношении R (но не на оборот). чаще записывают в виде aRb элементы a и b находятся в отношении R (но не на оборот).Отношение принадлежности элементы 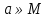 также можно рассматривать как бинарное отношение между объектами a и M, причём R(a,M), если также можно рассматривать как бинарное отношение между объектами a и M, причём R(a,M), если 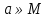 и не принадлежности R, если и не принадлежности R, если 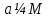 . .Бинарное отношение на конечных множествах можно представить кв. матрицей, строки и столбцы которой- элементы данного мн-ва, а элемент матрицы находящийся на пересечении строки X и столбца Y равен 1, если X и Y находятся в отношении R(XRY), и равен 0 если не находятся в отношении R. ((X,Y) 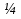 R) R)Запись ARB рассматривается, как совокупность всех высказываний элемента aЄA находится в отношении RaЄARbЄB. Отрицания отношения. Пусть aRb, отношение R , бинарным отношением 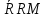 на мн-ве М наз. бинарное отношение в котором находятся все пары элементов мн-ва М кроме элементов находящихся в отношении R (противоположным). на мн-ве М наз. бинарное отношение в котором находятся все пары элементов мн-ва М кроме элементов находящихся в отношении R (противоположным).Какие бывают отношения:
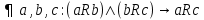 Транзитивным замкнутым бинарное отнош. Rназ.такое бинарное отношие 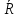 , что , что 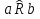 , если сущ. цепочка c1,…cn для которой имеет место след.нер-во aRc1,c1Rc2,…,cnRb , если сущ. цепочка c1,…cn для которой имеет место след.нер-во aRc1,c1Rc2,…,cnRb5.Отношение порядка. Отношение эквивалентн. Бинарные опер. Отношение эквивалентности наз. отнош., явл. рефлексивным, симметричным.и транзитивным. (X,Y) R (Z,P) X/Y=Z/P Пусть на мн-ве М задано отношение эквивалентности R, для каждого элемента 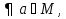 рассмотрим Ma ={b| рассмотрим Ma ={b|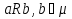 }. }.В силу симметричности и транзитивности отнош. R получаем, что если 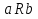 , то мн-ве Ma = Mb. , то мн-ве Ma = Mb.Если 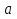 Ṝb, то Ma Ṝb, то Ma Mb= Mb= , следовательно система множеств { Ma } есть разбиение мн-ва М на классы эквивалентности бинарного отношения R на множестве М. При этом любые два элемента одного класса эквивалентности эквивалентны, любые 2 элемента разных классов не эквивалентны. , следовательно система множеств { Ma } есть разбиение мн-ва М на классы эквивалентности бинарного отношения R на множестве М. При этом любые два элемента одного класса эквивалентности эквивалентны, любые 2 элемента разных классов не эквивалентны.Отношения порядка. Отношения строгого порядка наз. бинарное отношение явл. антисимметричным, антирефлексивным и транзитивным. Обозначают это отношение таким образом a{b и говорят: а предшествует b. Отношения не строгого порядка наз. бинарное отношение явл. рефлексивным, антисимметричным и транзитивным. Отношения порядка устанавливаются на тех мн-вах, где для всех пар либо для некоторых отношение предшествования. Задание на мн-ве отношения порядка наз. Упорядочением мн-ва, а само мн-во М наз. упорядоченным. Если для a,b 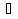 M выполнено a{b либо b{a, то элементы a и b наз. сравнимыми.В противном случае несравнимыми. M выполнено a{b либо b{a, то элементы a и b наз. сравнимыми.В противном случае несравнимыми. Линейноупорядоченным мн-вом М наз. мн-во на котором задано отнош. порядка, причём любые 2 элемента мн-ва М сравнимы. Частично упорядоченным наз. мн-во в котором допускается несравнимые элементы. Если a2+b2+c2 Бинарные операции. Множество 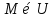 , B={0,1}, тогда отображение , B={0,1}, тогда отображение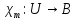 наз. характеристической ф-цией м-ва M и ставит в соответствие элементам множ. M 1 наз. характеристической ф-цией м-ва M и ставит в соответствие элементам множ. M 1 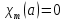 , и О если элемент , и О если элемент 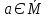 , то , то 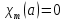 . .n-арная операция на множ. M-есть отображ.f :Mn→M, где М – произвольное множ. не обязательно числовое. Если n=2, то операция наз. бинарной 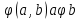 – обозначение. – обозначение.Частным случаем n- арной операции когда M – числовое множ. явл. n- местная функция. Мн-во М наз. замкнутым отнош. опер. 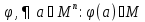 . .БулеаномB(E) наз.множ. Всех подмн-ств множ. E. БулеаномB(E) явл. Замкнутым отнош. операций объединения, пересечения и дополнения ( 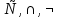 ). ).А система { B(E), 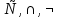 } – наз. алгеброй мн-ва на мн-ве Е или алгеброй Кантора. } – наз. алгеброй мн-ва на мн-ве Е или алгеброй Кантора.Ассоциативной бинарной операцией наз. опер. 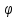 , обладающая св-вом: , обладающая св-вом: 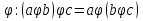 . . Ассоциативность позволяет записывать такую последов. без скобок. (32:4):2=4 32:(4:2)=16 Если опер. 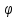 обладает св-вом: обладает св-вом: 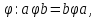 то она наз. коммутативной бинарной опер. то она наз. коммутативной бинарной опер.Дистрибутивность бинарной опер. определяет распределительный закон подобный арифметическому отношению ((a+b)c=ac+bc. Дистрибутивность слева бинарной опер. 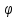 относ. бинарной опер. относ. бинарной опер. 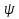 есть св-ва: есть св-ва: 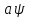 ( (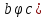 = =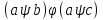 . .Дистрибутивность справа бинарной опер. 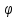 относ. бинарной опер. относ. бинарной опер. 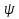 будет св-ва: будет св-ва: 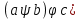 = =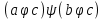 . .6. Алгебры. Алгебра Кантора и булева алгебра. Изоморфизм. Операции над двоичными числами. Алфавит, это кортеж попарных символов, которые мы будем наз. буквами алфавита. К алфавиту будем также относить мн-во {0,1}, а также {0,1,2,…,9}. Словом в алфавите A будем называть кортеж (вектор) из символов алфавита А. 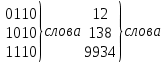 Слово записывается символами алфавита подряд слева направо без пробелов. Формула не всегда считается словом из-за нелинейности расположения символов. Алгеброй будем. наз. мн-во М вместе с заданной на этом мн-ве системой операций 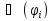 , где , где 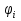 – некот. опер. При этом – некот. опер. При этом 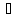 наз. сигнатурой алгебры, М – носитель алгебры. наз. сигнатурой алгебры, М – носитель алгебры.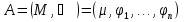 (F; D) – мно-во всех диф. фун. F многл. всех действ. ф-ций, D – оператор диф. Изоморфизмом 2-х алгебр А= 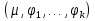 ; B=( ; B=(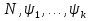 ) будем наз. взаимооднозначное соотв. Г между M и N и операциями ) будем наз. взаимооднозначное соотв. Г между M и N и операциями 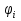 и и 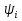 при котором выполнено усл.: при котором выполнено усл.: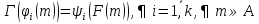 Смысл этого соответствия состоит в том, что если в алгебре А выполнить какие-либо операции над элементами мн-ва М и выполнить соотв. операции в алгебре В над элементами мн-ва М, то результат операции также будут соответствовать друг другу. Т.к. система 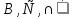 явл. алгеброй Кантора. Если явл. алгеброй Кантора. Если  этой алгебры поставить в соответствие этой алгебры поставить в соответствие  операцию операцию 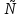 трактовать как +; трактовать как +;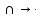 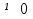 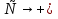 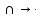 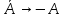 То алгебра Кантера будет соотв. алгебре введённой на мн-вецелых чисел отн. +,  ; ;Т.к. в изоморфных алгебрах А и В можно элементы и операции переименовать так, что В=А, то в дальнейшим алгебры будем рассматривать в точности до изоморфизма. |

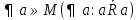
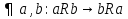
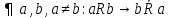 ,
,