Гдз общ. Элементы теории вероятностей Самостоятельная работа Вариант 1 Часть Тест
 Скачать 61.06 Kb. Скачать 61.06 Kb.
|
|
Элементы теории вероятностей Самостоятельная работа Вариант 1 Часть 1. Тест Под случайным событием, связанным с некоторым опытом, понимается всякое событие, которое при осуществлении этого опыта а) не может произойти; б) либо происходит, либо нет; в) обязательно произойдет. Вероятность достоверного события равна а) 0; б) 1; в) 2; г) 3. Из 25 экзаменационных билетов, занумерованных числами от 1 до 25, студент наудачу извлекает 1. Какова вероятность того, что студент сдаст экзамен, если он знает ответы на 23 билета? а) 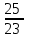 ; б) ; б) 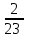 ; в) ; в) 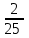 ; г) ; г) 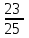 . .В коробке 10 шаров: 3 белых, 4 черных, 3 синих. Наудачу вытащили 1 шарик. Какова вероятность, что он будет либо белым, либо черным? а) 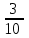 ; б) ; б) 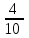 ; в) ; в) 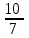 ; г) ; г) 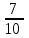 . .Из слова «математика» выбирается наугад одна буква. Какова вероятность того, что эта буква «а»? а) 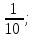 б) б) 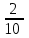 ; в) ; в) 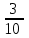 ; г) ; г) 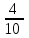 . .Часть 2 Решение задач Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками. В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке. Определите вероятность того, что при бросании кубика выпало число очков, не большее 3. В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку. Элементы теории вероятностей Самостоятельная работа Вариант 2 Часть 1. Тест Если событие происходит в данном опыте обязательно, то оно называется а) совместным; б) реальным; в) достоверным; г) невозможным. Если появление одного из событий не исключает появление другого в одном и том же испытании, то такие события называются а) совместными; б) несовместными; в) зависимыми; г) независимыми. Вероятность любого события есть неотрицательное число, не превосходящее а) 1; б) 2; в) 3; г) 4. Из слова «автоматика» выбирается наугад одна буква. Какова вероятность того, что это будет буква «а»? а) 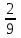 ; б) ; б) 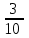 ; в) ; в) 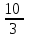 ; г) ; г) 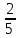 . .Магазин получил продукцию в 11 ящиках с трех складов: 4 с первого склада, 5 со второго склада, 2 с третьего склада. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик или с первого или со второго склада? А) 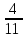 ; б) ; б) 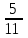 ; в) ; в) 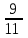 ; г) ; г) 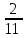 . . Часть 2 Решение задач Телевизор у Марины сломался и показывает только один случайный канал. Марина включает телевизор. В это время по восьми каналам из сорока показывают кинокомедии. Найдите вероятность того, что Марина попадет на канал, где комедия не идет. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с вишней. В фирме такси в данный момент свободно 15 машин: 3 чёрных, 6 жёлтых и 6 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси. В каждой пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдёт приз в своей банке. Определите вероятность того, что при бросании кубика выпало число очков, не большее 3. В магазине канцтоваров продаётся 200 ручек, из них 31 красная, 25 зелёных, 38 фиолетовых, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что при случайном выборе одной ручки будет выбрана красная или чёрная ручка. Элементы теории вероятностей Самостоятельная работа Вариант 3 Часть 1. Тест Если в данном опыте никакие два из событий не могут произойти одновременно, то такие события называются а) несовместными; б) невозможными; в) равносильными; г) совместными. В партии из 100 деталей 3 бракованных. Какова вероятность того, что взятая наудачу деталь окажется бракованной? а)  ; б) ; б) 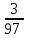 ; в) ; в) 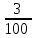 ; ; 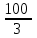 . .Вероятность невозможного события равна а) 0; б) 1; в) 2; г) 3. На полке в произвольном порядке расставлено 10 учебников. Из них 1 по математике, 2 по химии, 3 по биологии и 4 по географии. Студент произвольно взял 1 учебник. Какова вероятность того, что он будет либо по математике, либо по химии? а) 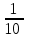 ; б) ; б) 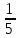 ; в) ; в) 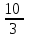 ; г) ; г) 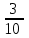 . .Если наступление события В не оказывает никакого влияния на вероятность наступления события А, и наоборот, наступление события А не оказывает никакого влияния на вероятность наступления события В, то события А и В называются а) несовместными; б) независимыми; в) невозможными; г) зависимыми. Часть 2 Решение задач Телевизор у Саши сломался и показывает только один случайный канал. Саша включает телевизор. В это время по пятнадцати каналам из пятидесяти показывают кинокомедии. Найдите вероятность того, что Саша попадет на канал, где комедия не идет. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с вишней. В фирме такси в данный момент свободно 15 машин: 4 черных, 3 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. В каждой четвертой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Аля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Аля не найдет приз в своей банке. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет менее 4 очков. В магазине канцтоваров продаётся 112 ручки, из них 17 – красные, 44 – зелёные, 29 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку. Элементы теории вероятностей Самостоятельная работа Вариант 4 Часть 1. Тест Если событие в данном опыте не может произойти, то оно называется а) невозможным; б) несовместным; в) необязательным; г) недостоверным. Вероятность невозможного события равна а) 0; б) 1; в) 2; г) 3. В магазин поступило 30 холодильников. 5 из них имеют заводской дефект. Случайным образом выбирается один холодильник. Какова вероятность, что он будет без дефекта? а) 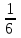 ; б) ; б)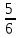 ; в) ; в) 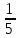 ; г) ; г) 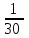 . .В классе 20 человек. Из них 5 отличников, 9 хорошистов, 3 имеют тройки и 3 имеют двойки. Какова вероятность того, что выбранный случайно ученик либо хорошист, либо отличник? а) 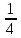 ; б) ; б) 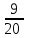 ; в) ; в) 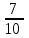 ; г) ; г) 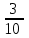 . .5. Вероятность достоверного события равна а) 0; б) 1; в) 2; г) 3. Часть 2 Решение задач Телевизор у Любы сломался и показывает только один случайный канал. Люба включает телевизор. В это время по двадцати пяти каналам из пятидесяти показывают кинокомедии. Найдите вероятность того, что Люба попадет на канал, где комедия не идет. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с вишней. В фирме такси в данный момент свободно 10 машин: 1 черная, 1 желтая и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. В каждой двадцать пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Коля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Коля не найдет приз в своей банке. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 4 очков. В магазине канцтоваров продаётся 206 ручек, из них 20 – красные, 8 – зелёные, 12 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или синюю ручку. |
