Билеты матан 1 курс 1 семестр Л. Мат.Анализ (Экзамен). Эпсилонокрестности
 Скачать 65.63 Kb. Скачать 65.63 Kb.
|
|
Эпсилон-окрестности: 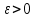 , равносильные записи , равносильные записи 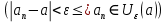 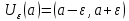 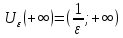 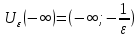 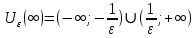 Определения предела последовательности: (1) Если есть конечные предел: 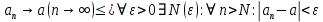 Остальное в пункте 5. 1. Сходящаяся последовательность и ее предел. Теорема об арифметических действиях с пределами. Замена переменной в пределе. 1) Сходящаяся последовательность – последовательность имеющая числовой предел. Def: Говорят, что последовательность 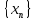 является сходящейся, если является сходящейся, если 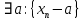 – бесконечно малая послед. Числа – бесконечно малая послед. Числа 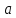 в этом случае называется пределом посл. в этом случае называется пределом посл. 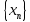 . .Def: Число 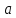 называется пределом посл. называется пределом посл. 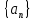 (пишут (пишут 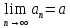 ), ), если 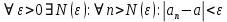 Теорема о единственности предела Если посл. 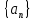 – сходящаяся, то предел единственный – сходящаяся, то предел единственныйДок-во: От противного, пусть 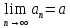 , , 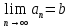 , => ( , => (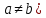 Распишем по опр. Предела: 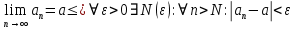 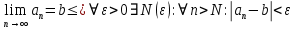 Возьмем произволный 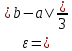 , , 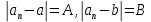 => и восполуемся свойством неравенства: => и восполуемся свойством неравенства: 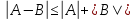 : : 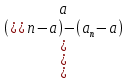 => 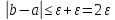 => подставит => подставит 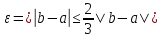 => противоречие, ЧТД. => противоречие, ЧТД.Теорема. Сходящиеся последовательности ограничены. 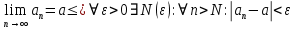 ––––––––| 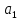 –––––––––| –––––––––|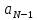 ––––––– –––––––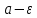 (––––|a––––) (––––|a––––)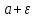 –––––––––| –––––––––|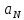 ––––| ––––|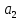 ––––––––– –––––––––Тогда возьмем число 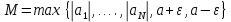 тогда тогда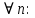 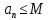 . Значит сход. посл. ограничена, мы получили определение огр посл. (так как за окрестностью a+e a-e – находится конечное количество членов последовательности, то в ней можно найти наибольший член, который и будет ограничивать всю эту последовательность.) . Значит сход. посл. ограничена, мы получили определение огр посл. (так как за окрестностью a+e a-e – находится конечное количество членов последовательности, то в ней можно найти наибольший член, который и будет ограничивать всю эту последовательность.)2) Расходящаяся последовательность – это последовательность, не имеющая конечного числого предела. Либо бесконечность. 3) Теорема Ариф.Действиях.Пределы: Пусть 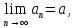 и и 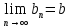 , , 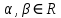 Тогда: (1) 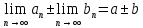 Док-во: Распишем по определению предела: 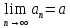 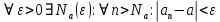 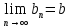 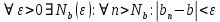 => Воспользуемся неравенством: 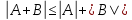 : :=> 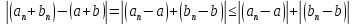 Теперь нам нужно найти такую функцию 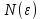 , при которой, для любого положительного числа , выполняется неравенство , при которой, для любого положительного числа , выполняется неравенство 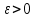 : :Положим 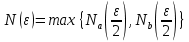 Тогда 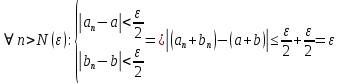 , ЧТД. , ЧТД.(2) 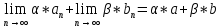 Док-во: Для того, чтобы доказать это, достаточно доказать свойство однородности: 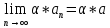 : :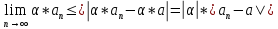 , положим , положим 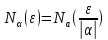 Тогда 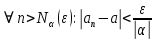 Тогда Тогда 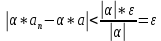 *Если 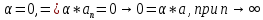 , ЧТД. , ЧТД.(3) 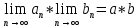 Док-во: 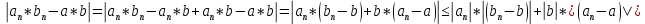 Где: 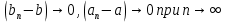 , , 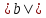 – постоянная значит – постоянная значит 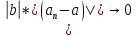 Тогда определим Что же такое 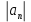 : По теореме об ограниченности сход. посл. => : По теореме об ограниченности сход. посл. => 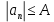 Тогда положим 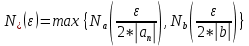 Тогда: 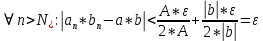 . ЧТД. . ЧТД.(4) 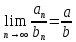 , при , при 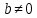 : Для того чтобы доказать это свойство, достаточно доказать что : Для того чтобы доказать это свойство, достаточно доказать что 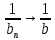 : :Док-во: 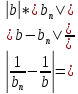 1. Положим 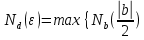 , тогда: , тогда: 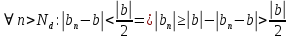 Тогда вернемся к  : :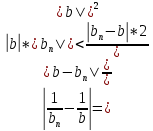 Значит следущим шагом до конца положим 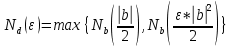 Значит получим что: 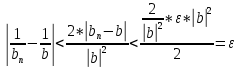 . ЧТД. . ЧТД.4) Замена переменной в пределе: 2. Фундаментальная последовательность. Вещественные числа как пополнение рациональных. Полнота множества вещественных чисел. 1)Фундаментальная последовательсноть – посл., где любые два члена последовательности друг от друга отличаются меньше чем на 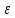 . .Def: 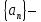 фунд. фунд. 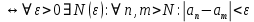 Теорема (Критерий КОШИ): Если 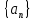 – сход. => – сход. => 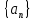 – фунд. – фунд.Доказательство: 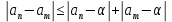 , фиксируем , фиксируем 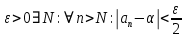 => Пусть m, n > N, ТОГДА 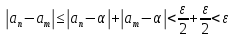 ЧТД. ЧТД.* –––––––––––––––––––– 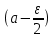 (–––––* (–––––*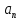 ––––––––*a–––––––* ––––––––*a–––––––*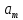 –––––)( –––––)(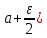 ––––––––––––––––– –––––––––––––––––Так как начиная с какого то номера все члены посл. оказались в этом интервале, это значит что 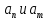 также в этом интервале, причем они отличаются друг от друга меньше чем на эпсилон. ЧТД также в этом интервале, причем они отличаются друг от друга меньше чем на эпсилон. ЧТД2) Вещественные числа как пополнение рациональных. Классы эквивалент в тетради синей (лекция 3) Вещественные числа Более точно, рассмотрим все фундаментальные последовательности рациональных чисел Две такие последовательности Множество вещественных чисел можно определить как классы эквивалентности этих последовательностей. 3) Полнота множества вещественных чисел. 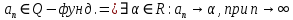 T. (Полнота R по метрике): (1) 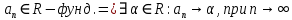 Док-во: 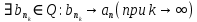 Рассмотрим посл. 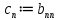 Тогда: 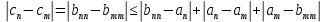 => 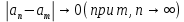 Добавляем тогда: к 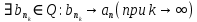 что что 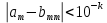 Тогда можем сказать, что 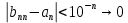 и и 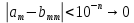 (2) 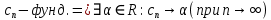 (3) Верни ли, что 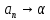 : :Рассмотрим 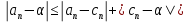 Где 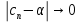 и и 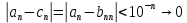 ЧТД. 3. Супремум и инфимум. Существование супремума и инфимума для произвольного подмножества вещественнных чисел. 1) Множество 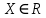 называется ограниченным сверху, если существует такое число b: называется ограниченным сверху, если существует такое число b: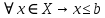 – число b ограничивает множество X сверху. – число b ограничивает множество X сверху.2) Множество 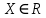 называется ограниченным снизу, если существует такое число a: называется ограниченным снизу, если существует такое число a: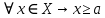 – число a ограничивает множество X снизу. – число a ограничивает множество X снизу.3) Следовательно, если взять любое число большее чем b или a, оно также будет является верхней или нижний гранью множества X, значит множество X имеет бесконечное количество верхних и нижних граней, и для нас главной будет наименьшая из них, то есть точная верхняя или нижняя грань M = supX / M = infX 4) Теорема о существовании точной ниж и верх граней.: Определение. Верхней гранью непустого множества X⊂R называется число b, удовлетворяющее условиям: ∀x∈X → x≤b; ∀b′ Определение. Нижней гранью непустого множества X⊂R называется число a, удовлетворяющее условиям: ∀x∈X → x≥a; ∀a′>a → ∃x∈X: x Доказательство. Пусть A - непустое ограниченное сверху множество. Рассмотрим непустое множество B, элементами которого являются все числа b, ограничивающие множество A сверху. Тогда ∀a∈A, ∀b∈B → a≤b Из аксиомы непрерывности (по дедекинду) следует, что для некоторого c∈R ∀a∈A, ∀b∈B → a≤c≤b Покажем, что ∃supA=c Первое условие из определения верхней грани выполнено для c в силу того, что ∀a∈A → a≤c Покажем, что выполняется и второе. Пусть c′ Следовательно, c=supA, и теорема доказана. 4) Теорема единственности. T. Числовое множество не может иметь больше одной точной верхней грани. Доказательство. Допуская противное, предположим, что каждое из чисел b и b′ (b≠b′) является верхней гранью множества X. Пусть, для определённости, b′ 4. Теорема о пределе монотонной последовательности. Теорема о зажатой последовательности (о двух милиционерах). 1) T. (Предел мон. Посл.) Пусть 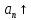 – посл. Возрастает, тогда – посл. Возрастает, тогда 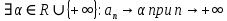 . .Если посл-ть возрастает, то у нее точно есть предел 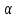 . .Док-во: 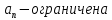 , то пределом будет число , то пределом будет число 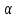 , если , если 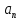 – неограничено, то – неограничено, то 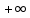 Возьмем число 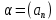 , следовательно из свойств sup получим: , следовательно из свойств sup получим:1) 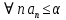 2) 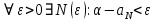 Мы доказали что если взять окрестность, то в этой окрестности найдется член последовательности который будет приближен к альфа. Теперь докажем что последовательность возрастает: Если 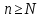 то в силу монотонности ( то в силу монотонности (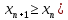 получим что получим что 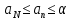 Значит 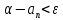 В итоге получим определение предела посл: В итоге получим определение предела посл: 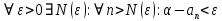 ЧТД ЧТД2) T. (Зажатая посл) Пусть есть 2-е посл. 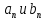 , и они оба сходятся к одному числу гамма, и пусть элементы посл. , и они оба сходятся к одному числу гамма, и пусть элементы посл. 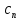 удовлетворяют условию, удовлетворяют условию, 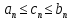 , ТОГДА , ТОГДА 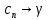 (также стремится к гамме). (также стремится к гамме).Док-во: Так как, посл. 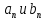 имеют конечные пределы, то по определению предела, следует, что: имеют конечные пределы, то по определению предела, следует, что: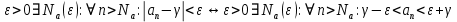 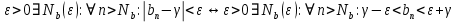 Имеется некоторое 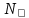 , такое что выполняется , такое что выполняется 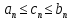 , следовательно положим что , следовательно положим что 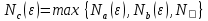 : :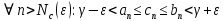 Следовательно 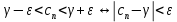 и это значит что и это значит что 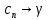 . ЧТД. . ЧТД.5. Бесконечно малая последовательность: классы o(1) и o(xn). Арифметические операции над бесконечно малыми. (1) Бесконечно малая последовательность – это сходящаяся последовательность, пределом которой является ноль: 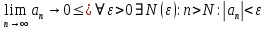 (2) Свойства бесконечно малой последовательности: Пусть 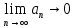 и и 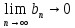 , ТОГДА: , ТОГДА:1) 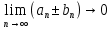 . Доказывается как и с обычными пределами. . Доказывается как и с обычными пределами.2) 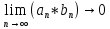 . Доказывается как и с обычными пределами. . Доказывается как и с обычными пределами.3) Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью: Пусть  Тогда: Тогда: 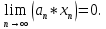 Док-во: 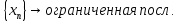 => => 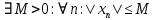 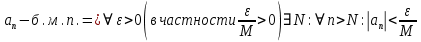 , , Тогда докажем, что 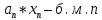 : :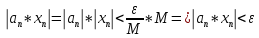 , ЧТД. , ЧТД.4) Свойство представления сходящейся последовательности через бесконечно малую: Для того, чтобы посл. 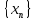 имела предел b, необходимо и достаточно, чтобы: имела предел b, необходимо и достаточно, чтобы: 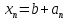 , где , где 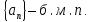 : :Док-во: 1. Необходимость: Пусть 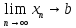 , тогда рассмотрим послед. , тогда рассмотрим послед. 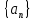 , с общим членом: , с общим членом: 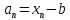 , => , => 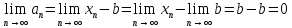 , значит послед. , значит послед. 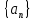 – б.м.п. – б.м.п.2. Достаточность: Пусть 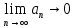 – б.м.п. Тогда по ариф. св-вам пределов имеем: – б.м.п. Тогда по ариф. св-вам пределов имеем: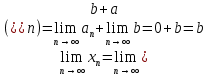 Следствия: 1) Произведение б.м.п на постоянную C – б.м.п. ( из свойства 3) 2) Производение б.м.п. на б.м.п. – б.м.п. (из свойства 3) (3) классы o(1) и o( 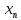 ): ):Если последовательность стремится к 0, это класс ( о малое (1)) Если последовательность стремится к 0 быстро, со скоростью не менее, чем какая то гарантированная, это класс ( о малое от чего нибудь) – o( 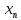 ) )(4) Бесконечно большая последовательности – последовательность, имеющая бесконечные предел, т.е. все ее члены безгранично возрастают. 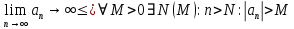 . .Def (Знаковая бесконечность): 1)  2)  Теорема: Если  – б.б.п и все ее члены отличны от нуля, то – б.б.п и все ее члены отличны от нуля, то  – б.м.п. и наоборот: – б.м.п. и наоборот: Док-во:  А это  . ЧТД. . ЧТД.6. Сходящийся ряд: определение, необходимый признак сходимости, теорема об арифметических действиях с пределом. Числовой ряд: Вид:  , где , где  –члены ряда. –члены ряда.Его записывают как  <=> <=>   – частичные суммы – частичные суммы**** Ряды нужны для того, чтобы устанавливать сам факт сходимость ряда, без использования значения альфа, а также определять скорость сходимости без того же альфа. Сходимость ряда: (1) Def: Будем говорить, что 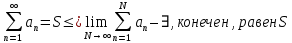 . (Ряд сходится, если тогда и только тогда, когда предел частичных сум . (Ряд сходится, если тогда и только тогда, когда предел частичных сум 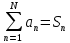 – – 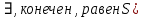 В этом случае можно также говорить что ряд что 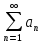 СХОДИТСЯ к S. СХОДИТСЯ к S.(2) В ином случае, если 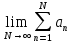 – не существует, или имеет бесконечные предел, то ряд что – не существует, или имеет бесконечные предел, то ряд что 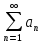 – РАСХОДИТСЯ. – РАСХОДИТСЯ.Def: 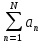 – частичная сумма – начальные члены ряда, без пропусков. – частичная сумма – начальные члены ряда, без пропусков.(3) Любую последовательность мы можем переформулировать в терминах ряда: Т.е. у нас есть посл. 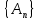 то по ней мы можем построить посл. то по ней мы можем построить посл. 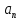 , такое что , такое что 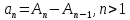 , , 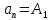 , , ТОГДА 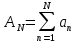 (последовательность частичных сумм ( (последовательность частичных сумм ( ) )(4) Теорема об арифмет. Действияхс пределами сходящихся рядов: Теорема: Пусть  – ряды сходятся, – ряды сходятся,  , тогда: , тогда:1)  (сумма каждого ряда будет (сумма каждого ряда будет 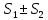 ) )2) 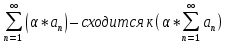 (сумма ряда будет равна (сумма ряда будет равна 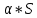 ) )Док-во: 1) Рассмотрим посл. 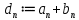 (общий член нашего 3 ряда, равен сумме общих членов ряда 1 и 2), ТОГДА (общий член нашего 3 ряда, равен сумме общих членов ряда 1 и 2), ТОГДА 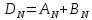 ( последовательность частичных сумм ряда 3 равна сумме последовательностей частичных сумм ряд 1 и 2), значит по определению ряда, мы можем написать предел) => ( последовательность частичных сумм ряда 3 равна сумме последовательностей частичных сумм ряд 1 и 2), значит по определению ряда, мы можем написать предел) => 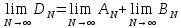 , где , где 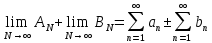 . .Значит мы нашли предел 3 ряда, при котором он будет сходится и равен сумме рядов 1 и 2. ЧТД. 2) Пусть 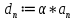 => => 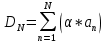 , и так как сумма конечна из за N, то: , и так как сумма конечна из за N, то:=> 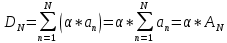 => => 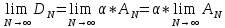 . . Где 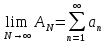 . .Значит мы нашли предел ряда 3, при котором он будет сходится, и сходится к константе умноженной на ряд 1. ЧТД. (5) Достаточный признак сходимости: 1) 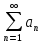 – сход. => – сход. => 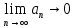 2) 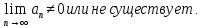 => => 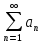 – расходится – расходитсяДок-во: 1) Пусть: 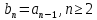 и и 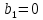 , тогда: , тогда: 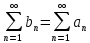 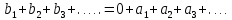 Тогда  Вычтем ряды a и b:  , , также это можно записать как:  , ЧТД. , ЧТД.2) От противного, предположим что  => => 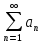 – сходится, – сходится,но т.к. ряд сходится, значит, то по тому что мы доказали в пункте 1, 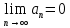 , возникает противоречие, следовательно ряд расходится. ЧТД. , возникает противоречие, следовательно ряд расходится. ЧТД.7. Абсолютно сходящийся ряд: определение, теорема сравнения, шкала геометрических прогрессий, шкала рядов Дирихле. (1) Определение Абсолютно сход. ряда: Def: ряд 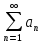 – называется абсолютно сходящимся, тогда и только тогда, когда ряд – называется абсолютно сходящимся, тогда и только тогда, когда ряд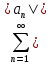 – сходится. – сходится.Связь сходимости ряда и абсолютной сходимости: Теорема: Если ряд 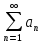 – сходится абсолютно, то он – сходится абсолютно, то он 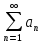 – сходится. – сходится.Док-во: Пусть есть послед-ти: 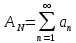 и и 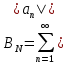 , т.к. , т.к.   – фундаментальная посл. <=> – фундаментальная посл. <=>  Рассмотрим такое:  , не умоляю общности считаем что: , не умоляю общности считаем что:  ТОГДА: ТОГДА:  (т.к. M>N то можем заменить  ) )Значит:  – фунд., => – фунд., =>  – сходится <=> – сходится <=>  – сходится. – сходится.8. Абсолютно сходящийся ряд: определение, теорема сравнения, признак Коши, признак Даламбера. 9. Условно сходящийся ряд. Признак Лейбница. 10. Сходимость ряда, зависящего от параметра (переменной). Область сходимости, абсолютной сходимости, условной сходимости. Теорема Абеля для степенного ряда. 11. Предел функции: определения на языке последовательностей(Гейне) и на языке окрестностей(Коши) (в конечной и бесконечной точке для конечного и бесконечного значения пределов). Арифметические действия с пределами. Замена переменной в пределе. 12. Непрерывность функции: определения на языке последовательностей и на языке окрестностей (в конечной и бесконечной точке для конечного и бесконечного значения пределов). Арифметические действия с непрерывными функциями. Непрерывность композиции непрерывных функций. 14. Теорема Больцано. 1) Подпоследовательность: Пусть  – посл-ть., тогда – посл-ть., тогда  при k = 1, 2, … – бесконечная посл, причем возрастающая, тогда при k = 1, 2, … – бесконечная посл, причем возрастающая, тогда  подпослед. подпослед.  2) Частичный предел  , причем , причем  может не иметь предела. может не иметь предела.Def 1:  Def 2: ––––––––––––––––––––––(––––|a–––)–––––––––––––––– В окрестности а лежит беск. Членов посл.  . .3) Приступим к теореме Больцано-Вейерштрасса: T. Из любой ограниченной последовательности, можно выделить сходящуяся подпоследовательность (т.е. имеющую предел).   Док-во: Возьмем огранич. посл.  , в которой количество членов бесконечно много. Далее поделим ее на 2 части, так, что хотя бы в одной из них количество членов бесконечно много: , в которой количество членов бесконечно много. Далее поделим ее на 2 части, так, что хотя бы в одной из них количество членов бесконечно много:––––––––––––––[––––––––––––|––––––––––]––––––––––––––––––– Возьмем правый отрезок и поделим еще раз на 2, и так делаем несколько раз, в итоге получим: ––––––––––––––[––––––––––––[––]–––]–––––]––––––––––––––––––– 2) По теореме о вложенных отрезках (принцип Коши-Кантора) для любой системы вложенных отрезков у нас существует точка, назовем ее A, такая что она принадлежит всем нашим отрезкам. 3) Соберем подпоследовательность, которая будет сходится к точке A: Возьмем  член, который лежит на 1 отрезке: член, который лежит на 1 отрезке:––––––––––––––[––––––––––––[––]–––]––  –––]––––––––––––––––––– –––]–––––––––––––––––––Тогда во 2 отрезке, найдется такой член, номер которого будет больше предыдущего (  ): ):––––––––––––––[––––––––––––[––]–  ––]–– ––]–– –––]––––––––––––––––––– –––]–––––––––––––––––––Он в любом случае найдется, т.к. на каждом отсеченном отрезке беск. много членов посл. Далее, получается подпоследовательность:  4) Докажем что эта подпоследовательсноть сходится к A: Назовем первый отсеч. отрезок – M, тогда 1.  2. 2. 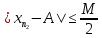 Значит: 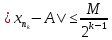 , что также можно записать как: , что также можно записать как: 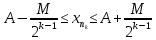 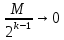 , т.к. любая посл. вида , т.к. любая посл. вида  , значит левая и правая часть стремится к A, а по теореме о 2-ух милиционерах и , значит левая и правая часть стремится к A, а по теореме о 2-ух милиционерах и  . ЧТД. . ЧТД.15. Теорема Вейерштрасса. T. Функция, непрерывная на отрезке, ограничена и достигает своей верх и ниж границы. Пусть f c ( [a,b] ) Тогда: (1)  – Функция ограничена. – Функция ограничена.(1) Док-во: От противного, допустим f – не ограничена:  Возьмём некоторые М:  ; ;   Получили последовательность точек из отрезка [a,b]. Но т.к. посл находится в промежутку [a,b] => эта посл. – ограничена, => по т. Больцано Вейерштрасса, из этой ограниченной последовательности можно выделить сходящуяся подпоследовательность, значит  Т.к.  – лежит в отрезку [a,b] ( – лежит в отрезку [a,b] ( ), значит в силу свойств предела – ), значит в силу свойств предела –  . .Значит по определению предела в терминах Гейна: Если  и f непрерывна, и f непрерывна, =>  . Однако . Однако  – это конкретное число, а в начале мы сказали что f – неограничена, тогда – это конкретное число, а в начале мы сказали что f – неограничена, тогда  и не может и не может  , значит возникает противоречие, => f – ограничена, ЧТД. , значит возникает противоречие, => f – ограничена, ЧТД.(2) 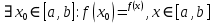 ( Достигает своей верх или ниж грани) ( Достигает своей верх или ниж грани)(2) Док-во: Т.к. ранее мы доказали, что f – непрерывна и ограничена на отрезку [a,b] => sup f(x) – число. Тогда, пусть 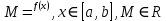 . .Из это мы знаем: 1) 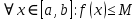 2) 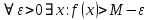 (Если чуть чуть отступить, сразу же найдется член последовательности) (Если чуть чуть отступить, сразу же найдется член последовательности)Тогда возьмём  , ,  Мы понимаем, что  – посл. ограничена, то по теореме Больцано-Вейерштрасса получаем следущее: – посл. ограничена, то по теореме Больцано-Вейерштрасса получаем следущее: => =>  Мы понимаем, что  => и т.к. => и т.к.  = >  ( ( 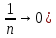 => по правая и левая часть стремится к M, тогда по теореме о двух милиционерах => => по правая и левая часть стремится к M, тогда по теореме о двух милиционерах => 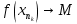 => => 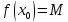 . ЧТД. . ЧТД.Тоже самое справедливо и для нижней границы. 16. Дифференцируемая функция: определения, теорема об арифметических действиях с дифференцируемыми функциями, теорема о дифференцировании композиции функций. 17. Теорема Ферма. 18. Теорема Ролля. Теорема Лагранжа. 19. Теорема Коши. Теорема Лопиталя. 20. Интерполяционный многочлен. Оценка погрешности интерполяции. 21. Многочлен Тейлора: определение, явный вид, свойства. Формула Тейлора с остатками в форме Пеано и в форме Лагранжа. |
