Лекции. Фактор времени в финансовокоммерческих расчетах
 Скачать 355.33 Kb. Скачать 355.33 Kb.
|
|
Расчет процентов с использованием процентных чисел В банковской практике размещенный на длительное время капитал может в течение этого периода времени изменяться, т.е. увеличиваться или уменьшаться путем дополнительных взносов или отчислений. Таким образом, при обслуживании счетов банки сталкиваются с непрерывной сетью поступлений и расходованием средств и начислением процентов на постоянно меняющуюся сумму. В этой ситуации в банковской практике используется правило: общая начисленная за весь срок сумма процентов равна сумме процентов, начисленных на каждую из постоянных на некотором отрезке времени сумм. Это касается и дебетовой, и кредитовой части счета. Разница лишь в том, что кредитовые проценты вычитаются. В таких случаях для расчета процентов используется методика расчета с вычислением процентных чисел: каждый раз, когда сумма на счете изменяется, производится расчет "процентного числа" за период, в течение которого сумма на счете была неизменной. Процентное число вычисляется по формуле: Процентное число = (Сумма на счете • Длительность периода в днях) / 100 = (PV • t) / 100 Для определения суммы процентов за весь срок их начисления все "процентные числа" складываются, и их сумма делится на постоянный делитель, который носит название "процентный ключ" или дивизор, определяемый отношением количества дней в году к годовой процентной ставке: I = ΣПроцентных чисел : Постоянный делитель, где Постоянный делитель =Продолжительность года в днях / Годовая ставка процентов = T / i 4) Проценты, вычисляемые с использованием дивизора, рассчитанного исходя из 365 дней в году, будут меньше, чем проценты по дивизору, где количество дней в году принято за 360, поэтому при обслуживании конкретного клиента всегда используется один из дивизоров. Методика с использованием процентных чисел по своей сути является последовательным применением формулы простых процентов для каждого интервала постоянства суммы на счете: I = I1 + I2 + I3 = P1 • t1 / T • i + P2 • t2 / T • i + P3 • t3 / T • i Переменные ставки Ставка процентов не является застывшей на вечные времена величиной, поэтому в финансовых операциях, в силу тех или иных причин, предусматриваются дискретно изменяющиеся во времени процентные ставки. Например, наличие инфляции вынуждает собственника денег периодически варьировать процентной ставкой. В таких случаях наращенную сумму определяют, используя следующую формулу: FV = PV • (1 + n1 • i1 + n2 • i2 + … + nk • ik), где k – количество периодов начисления; nk – продолжительность k-го периода; ik – ставка процентов в k-ом периоде. Определение срока ссуды и величины процентной ставки В любой простейшей финансовой операции всегда присутствуют четыре величины: современная величина (PV), наращенная или будущая величина (FV), процентная ставка (i) и время (n). Иногда при разработке условий финансовой сделки или ее анализе возникает необходимость решения задач, связанных с определением отсутствующих параметров, таких как срок финансовой операции или уровень процентной ставки. Как правило, в финансовых контрактах обязательно фиксируются сроки, даты, периоды начисления процентов, поскольку фактор времени в финансово-коммерческих расчетах играет важную роль. Однако бывают ситуации, когда срок финансовой операции прямо в условиях финансовой сделки не оговорен, или когда данный параметр определяется при разработке условий финансовой операции. Обычно срок финансовой операции определяют в тех случаях, когда известна процентная ставка и величина процентов. Если срок определяется в годах, то n = (FV - PV) : (PV • i), а если срок сделки необходимо определить в днях, то появляется временная база в качестве сомножителя: t = [(FV - PV) : (PV • i)] • T. Необходимость определения уровня процентной ставки возникает в тех случаях, когда она в явном виде в условиях финансовой операции не участвует, но степень доходности операции по заданным параметрам можно определить, воспользовавшись следующими формулами: i = (FV - PV) : (PV • n) = [(FV - PV) : (PV • t)] • T. Формула сложных процентов В финансовой практике значительная часть расчетов ведется с использованием схемы сложных процентов. Применение схемы сложных процентов целесообразно в тех случаях, когда: проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов; срок ссуды более года. Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга: FV = PV + I = PV + PV • i = PV • (1 + i) – за один период начисления; FV = (PV + I) • (1 + i) = PV • (1 + i) • (1 + i) = PV • (1 + i)2 – за два периода начисления; отсюда, за n периодов начисления формула примет вид: FV = PV • (1 + i)n = PV • kн , где FV – наращенная сумма долга; PV – первоначальная сумма долга; i – ставка процентов в периоде начисления; n – количество периодов начисления; kн – коэффициент (множитель) наращения сложных процентов. Эта формула называется формулой сложных процентов. Как было выше указано, различие начисления простых и сложных процентов в базе их начисления. Если простые проценты начисляются все время на одну и ту же первоначальную сумму долга, т.е. база начисления является постоянной величиной, то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу. Таким образом, простые проценты по своей сути являются абсолютными приростами, а формула простых процентов аналогична формуле определения уровня развития изучаемого явления с постоянными абсолютными приростами. Сложные проценты характеризуют процесс роста первоначальной суммы со стабильными темпами роста, при наращении ее по абсолютной величине с ускорением, следовательно, формулу сложных процентов можно рассматривать как определение уровня на базе стабильных темпов роста. Согласно общей теории статистики, для получения базисного темпа роста необходимо перемножить цепные темпы роста. Поскольку ставка процента за период является цепным темпом прироста, то цепной темп роста равен: (1 + i). Тогда базисный темп роста за весь период, исходя из постоянного темпа прироста, имеет вид: (1 + i)n . Базисные темпы роста или коэффициенты (множители) наращения, зависящие от процентной ставки и числа периодов наращения, табулированы и представлены в Приложении 2. Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через n периодов при заданной процентной ставке i. 5) Наращение по простым и сложным процентам Графическая иллюстрация соотношения наращенной суммы по простым и сложным процентам представлена на рисунке 4. 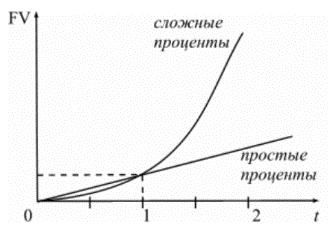 Рис.1. Наращение по простым и сложным процентам. Как видно из рисунка 4, при краткосрочных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам значительно выше, чем по простым. При любом i, если 0 < n < 1, то (1 + ni) > (1 + i)n ; если n > 1, то (1 + ni) < (1 + i)n ; если n = 1, то (1 + ni) = (1 + i)n . Таким образом, для лиц, предоставляющих кредит: более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года); более выгодной является схема сложных процентов, если срок ссуды превышает один год; обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов. Достаточно часто финансовые контракты заключаются на период, отличающийся от целого числа лет. В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием двух методов: общий метод заключается в прямом расчете по формуле сложных процентов: V = PV • (1 + i)n, n = a + b, где n – период сделки; a – целое число лет; b – дробная часть года. смешанный метод расчета предполагает для целого числа лет периода начисления процентов использовать формулу сложных процентов, а для дробной части года – формулу простых процентов: FV = PV • (1 + i)a • (1 + bi). Поскольку b < 1, то (1 + bi) > (1 + i)a, следовательно, наращенная сумма будет больше при использовании смешанной схемы. Номинальная ставка процентов Период начисления по сложным процентам не всегда равен году, однако в условиях финансовой операции указывается не ставка за период, а годовая ставка с указанием периода начисления – номинальная ставка ( j ). Номинальная ставка – годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год. Эта ставка: во-первых, не отражает реальной эффективности сделки; во-вторых, не может быть использована для сопоставлений. Если начисление процентов будет производиться m раз в год, а срок долга – n лет, то общее количество периодов начисления за весь срок финансовой операции составит: N = n • m Отсюда формулу сложных процентов можно записать в следующем виде: FV = PV • (1 + j / m)N = P • (1 + j /m)mn , где j – номинальная годовая ставка процентов. Пример. Изменим условия предыдущего примера, введя ежеквартальное начисление процентов. Решение: Количество периодов начисления: N = m • n = 4 • 2 = 8 Наращенная сумма составит: FV = PV • (1 + j / m)mn = 2'000 • (1 + 0,1 / 4 )8 = 2'436,81 руб. Сумма начисленных процентов: I = FV - PV = 2'436,81 - 2'000 = 436,81 руб. Таким образом, через два года на счете будет находиться сумма в размере 2'436,81 руб., из которой 2'000 руб. является первоначальной суммой, размещенной на счете, а 436,81 руб. – сумма начисленных процентов. Эффективная ставка Наряду с номинальной ставкой существует эффективная ставка (effective rate), измеряющая тот реальный относительный доход, который получен в целом за год, с учетом внутригодовой капитализации. Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m-разовое наращение в год по ставке j / m: (1 + i)n = (1 + j / m)mn, следовательно, i = (1 + j / m)m - 1. Из формулы следует, что эффективная ставка зависит от количества внутригодовых начислений. Расчет эффективной ставки является мощным инструментом финансового анализа, поскольку ее значение позволяет сравнивать между собой финансовые операции, имеющие различные условия: чем выше эффективная ставка финансовой операции, тем (при прочих равных условиях) она выгоднее для кредитора. Пример. Рассчитаем эффективную ставку для финансовой операции, рассмотренной в предыдущем примере, а также для вклада при ежемесячном начислении процентов по годовой ставке 10%. Решение: Эффективная ставка ежеквартального начисления процентов, исходя из 10% годовых, составит: i = (1 + j / m)m - 1 = (1 + 0,1 / 4)4 - 1 = 0,1038. Эффективная ставка ежемесячного начисления процентов будет равна: i = (1 + j / m)m - 1 = (1 + 0,1 / 12)12 - 1 = 0,1047. Таким образом, годовая ставка, эквивалентная номинальной ставке процентов в размере 10% годовых при ежемесячном начислении процентов, составит 10,47% против 10,38% с ежеквартальным начислением процентов. Чем больше периодов начисления, тем быстрее идет процесс наращения. Для облегчения расчетов можно пользоваться таблицами коэффициентов наращения сложных процентов, но внимательно следить за соответствием длины периода начисления и процентной ставки за этот же период. Например, если периодом начисления является квартал, то в расчетах должна использоваться квартальная ставка Непрерывное начисление процентов Все ситуации, которые мы до сих пор рассматривали, относились к дискретным процентам, поскольку их начисление осуществляется за фиксированные промежутки времени (год, квартал, месяц, день, час). Но на практике нередко встречаются случаи, когда проценты начисляются непрерывно, за сколь угодно малый промежуток времени. Если бы проценты начислялись ежедневно, то годовой коэффициент (множитель) наращения выглядел так: kн = (1 + j / m)m = (1 + j / 365)365 Но поскольку проценты начисляются непрерывно, то m стремится к бесконечности, а коэффициент (множитель) наращения стремится к ej: где e≈2,718281, называется числом Эйлера и является одной из важнейших постоянных математического анализа. Отсюда можно записать формулу наращенной суммы для n лет: FV = PV • e j • n = P • e δ • n Ставку непрерывных процентов называют силой роста (force of interest) и обозначают символом δ, в отличие от ставки дискретных процентов ( j ). Пример. Кредит в размере на 100 тыс. долларов получен сроком на 3 года под 8% годовых. Определить сумму подлежащего возврату в конце срока кредита, если проценты будут начисляться: а) один раз в год; б) ежедневно; в) непрерывно. Решение: Используем формулы дискретных и непрерывных процентов: начисление один раз в год: FV = 100'000 • (1 + 0,08)3 = 125'971,2 долларов; ежедневное начисление процентов: FV = 100'000 • (1 + 0,08 / 365)365 • 3 = 127'121,6 долларов непрерывное начисление процентов: FV = 100'000 • e 0,08 • 3 = 127'124,9 долларов. Графически изменение наращенной суммы в зависимости от частоты начисления имеет следующий вид: 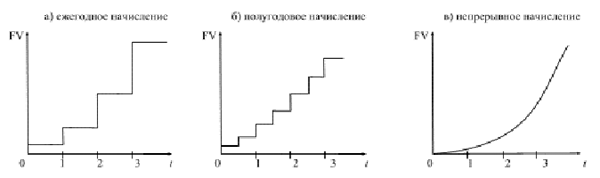 Рис. 1. Различные варианты начисления процентов При дискретном начислении каждая "ступенька" характеризует прирост основной суммы долга в результате очередного начисления процентов. Обратите внимание, что высота "ступенек" все время возрастает. В рамках одного года одной "ступеньке" на левом графике соответствует две "ступеньки" на среднем графике меньшего размера, но в сумме они превышают высоту "ступеньки" однократного начисления. Еще более быстрыми темпами идет наращение при непрерывном начислении процентов, что и показывает график справа. Таким образом, в зависимости от частоты начисления процентов наращение первоначальной суммы осуществляется с различными темпами, причем максимально возможное наращение осуществляется при бесконечном дроблении годового интервала. Непрерывное начисление процентов используется при анализе сложных финансовых задач, например, обоснование и выбор инвестиционных решений. Оценивая работу финансового учреждения, где платежи за период поступают многократно, целесообразно предполагать, что наращенная сумма непрерывно меняется во времени и применять непрерывное начисление процентов. Определение срока ссуды и величины процентной ставки Так же как для простых процентов, для сложных процентов необходимо иметь формулы, позволяющие определить недостающие параметры финансовой операции: срок ссуды: n = [log (FV / PV)] / [log (1 + i)] = [log (FV / PV) ] / [log(1 + j / m)m]; ставка сложных процентов: Пример. Что выгоднее: увеличение вклада в три раза за три года или 46% годовых? Решение: Такого рода задачи приходится решать не только лицам, занимающимся финансовой работой, но и населению, когда решается вопрос о том, куда выгоднее вложить деньги. В таких случаях решение сводится к определению процентной ставки: Таким образом, увеличение вклада за три года в три раза эквивалентно годовой процентной ставке в 44,3%, поэтому размещение денег под 46% годовых будет более выгодно. Сущность дисконтирования В финансовой практике часто приходится решать задачи, обратные определению наращенной суммы: по уже известной наращенной сумме (FV) следует определить неизвестную первоначальную сумму долга (PV). Такие ситуации возникают при разработке условий финансовой сделки, или когда проценты с наращенной суммы удерживаются непосредственно при выдаче ссуды. Процесс начисления и удержания процентов вперед, до наступления срока погашения долга, называют учетом, а сами проценты в виде разности наращенной и первоначальной сумм долга дисконтом (discount): D = FV - PV Термин дисконтирование в широком смысле означает определение значения стоимостной величины на некоторый момент времени при условии, что в будущем она составит заданную величину. 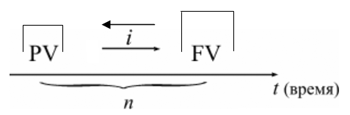 Рис. 1. Логика финансовой операции дисконтирования. Не редко такой расчет называют приведением стоимостного показателя к заданному моменту времени, а величину PV называют приведенной (современной или текущей) величиной FV. Таким образом, дисконтирование – приведение будущих денег к текущему моменту времени, и при этом не имеет значения, имела ли место в действительности данная финансовая операция или нет, а также независимо от того, можно ли считать дисконтируемую сумму буквально наращенной. Именно дисконтирование позволяет учитывать в стоимостных расчетах фактор времени, поскольку дает сегодняшнюю оценку суммы, которая будет получена в будущем. Привести стоимость денег можно к любому моменту времени, а не обязательно к началу финансовой операции. Исходя из методики начисления процентов, применяют два вида дисконтирования: математическое дисконтирование по процентной ставке; банковский учет по учетной ставке. Различие в ставке процентов и учетной ставке заключается в различии базы для начислений процентов: в процентной ставке в качестве базы берется первоначальная сумма долга: i = (FV - PV) / PV в учетной ставке за базу принимается наращенная сумма долга: d = (FV - PV) / FV Проценты, начисленные по ставке процентов, называются антисипативными, а по учетной ставке – декурсивными. Учетная ставка более жестко отражает временной фактор, чем процентная ставка. Если сравнить между собой математическое и банковское дисконтирование в случае, когда процентная и учетная ставка равны по своей величине, то видно, что приведенная величина по процентной ставке больше приведенной величины по учетной ставке. |
