Лекции. Фактор времени в финансовокоммерческих расчетах
 Скачать 355.33 Kb. Скачать 355.33 Kb.
|
|
Современная (текущая) величина ренты (аннуитета) Помимо наращенной суммы обобщающей характеристикой потока платежей является современная величина. Современная (текущая) величина потока платежей (капитализированная или приведенная величина) – это сумма платежей, дисконтированных на момент начала ренты по ставке начисляемых сложных процентов. Это важнейшая характеристика финансового анализа, т.к. является основой для измерения эффективности различных финансово-кредитных операций, сравнения условий контрактов и т.п. Данная характеристика показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые начислялись бы установленные проценты в течение всего срока, можно было бы получить указанную наращенную сумму. 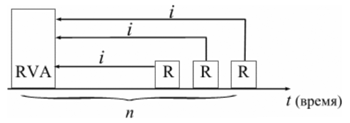 Рис. 1. Логика финансовой операции определения современной величины потока платежей. В этом случае реализуется схема дисконтирования: все элементы с помощью дисконтных множителей приведены к одному моменту времени, что позволяет их суммировать. В простейшем случае, для годовой обычной ренты с выплатами в конце каждого года, когда момент оценки совпадает с началом ренты, современная величина финансовой ренты равна: 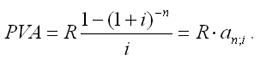 Дробь в формуле – коэффициент приведения ренты (an;i), значения которого табулированы для широкого круга значений, поскольку зависят от ставки процентов (i) и от числа лет (n) (Приложение 5). Пример. Определить по данным примера современную величину ренты. Решение: Современная величина ренты составит: Таким образом, все производимые в будущем платежи оцениваются в настоящий момент в размере 1'217,78 руб. Рассмотрим расчет современной величины ренты для различных ее видов: годовая рента с начислением процентов несколько раз в год: срочная рента при начислении процентов один раз в год: срочная рента с неоднократным начислением процентов в течение года, при условии, что число выплат не равно числе начислений, т.е. p ≠ m : Определение параметром ренты (аннуитета) Последовательные платежи в виде постоянной обычной годовой ренты определяются основными параметрами: R – размер платежа; n – срок ренты в годах; i – годовая ставка процентов. Однако при разработке условий финансовой операции могут возникать ситуации, когда заданной величиной является одна из двух обобщающих характеристик и неполный набор параметров ренты. В таких случаях находят недостающий параметр. Определение параметром ренты (аннуитета) При определении члена ренты возможны два варианта, зависящие от того, какая величина является сходной: а) наращенная сумма. Если сумма долга определена на какой-либо момент в будущем (FVA), тогда величину последующих взносов в течение n лет при начислении на них процентов по ставке i можно определить по формуле: Пример. Для покупки автомобиля через 5 лет потребуется 50 тыс. руб. Определите размер ежегодных взносов, вносимых в конце каждого года в банк, который начисляет проценты по ставке 40%. Решение: В данном случае известна наращенная величина постоянной финансовой ренты, поэтому размер ежегодных взносов будет равен: Таким образом, чтобы накопить на счете необходимую сумму для покупки автомобиля следует в конце каждого года в течении пяти лет откладывать 4'568 руб. б) современная величина финансовой ренты, тогда, исходя из ставки процента и срока ренты, разовый платеж находится по формуле: Пример. Сумма 10 тыс. долларов предоставлена в долг на 5 лет под 8% годовых. Определить ежегодную сумму погашения долга. Решение: Известна современная величина долга, отсюда: Таким образом, ежегодно необходимо будет возвращать сумму 2'504,56 руб. Можно произвести проверку: сумма долга с начисленными на нее процентами к концу пятого года будет составлять: FV = 10'000 • (1 + 0,08)5 = 14'693,28 руб. Наращенная сумма для потока платежей размером 2'504,56 руб. составит: Следовательно, величина члена финансовой ренты определена верно. Незначительное расхождение вызвано округлением расчетов. Современная величина ренты пренумерандо рассчитывается путем умножения современной величины обычной ренты на соответствующий множитель наращения Оценка некоторых видов ренты Если денежные поступления осуществляются достаточно длительное время и их число заранее не может быть известно, то такой поток называется бессрочным аннуитетом или вечной рентой. В этом случае определение будущей величины такого аннуитета не имеет смысла. Для данного вида финансовой ренты имеет смысл только характеристика современной величины потока платежей. Поток, даже с неограниченным числом платежей все же имеет конечную приведенную стоимость, поскольку с финансовой точки зрения, деньги, поступающие через много лет, сейчас практически ничего не стоят. Для бессрочного аннуитета постнумерандо формула современной величины принимает следующий вид: 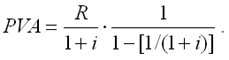 При больших сроках аннуитета и большом уровне процентной ставки для определения приведенной величины срочного аннуитета можно пользоваться формулой бессрочного аннуитета, поскольку полученный приблизительный результат не слишком будет отличаться от точного значения, т.к. при сроке более 40-50 лет коэффициенты дисконтирования аннуитета незначительно отличаются друг от друга. Приведенная стоимость бессрочного аннуитета пренумерандо в общем виде определяется из приведенной стоимости бессрочного аннуитета постнумерандо, скорректированного на коэффициент (1 + i), т.е. отличается на величину первого платежа. Непрерывный аннуитет (рента) Если промежутки между последовательными поступлениями являются бесконечно малой величиной, то такой аннуитет считают непрерывным, т.е. денежные поступления происходят непрерывно с постоянной интенсивностью. При начислении непрерывных процентов для получения формул определения наращенной или современной величины потока платежей необходимо перейти к пределу, откуда: наращенная величина потока платежей 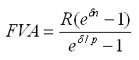 где σ – сила роста. современная величина потока платежей 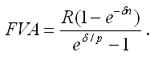 Особенности инвестиционных процессов как объекта финансовой математики Инвестиции – это долгосрочные финансовые вложения экономических ресурсов с целью создания и получения выгоды в будущем, которая должна быть выше начальной величины вложений. Инвестиционный процесс – это последовательность связанных инвестиций, растянутых во времени, отдача от которых также распределена во времени. Этот процесс характеризуется двусторонним потоком платежей, где отрицательные члены потока являются вложениями денежных средств в инвестиционный проект, а положительные члены потока – доходы от инвестированных средств. 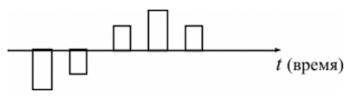 Рис. 1. Графическое изображение инвестиционного процесса Принято различать: финансовые инвестиции; реальные инвестиции; инвестиции в нематериальные активы. Финансовые инвестиции – вложение денежных средств в ценные бумаги; реальные инвестиции – вложения в основной капитал и прирост запасов; вложения в нематериальные активы – вложения в развитие научных исследований, повышение квалификации работников, приобретение лицензий и прав. Реализация инвестиционных проектов требует отказа от денежных средств сегодня в пользу получения дохода в будущем, поэтому любой инвестиционный проект требует анализа и оценки. Оценивая эффективность инвестиционных проектов, следует учитывать и степень риска, – здесь, как правило, выделяют два вида риска: предпринимательский и финансовый. Предпринимательский риск – риск, связанный с деятельностью конкретного бизнеса. Финансовый риск – изменениями рыночной ставки дохода на капитал. Для упрощения исследования эффективности инвестиций предполагается, что необходимая норма прибыли задана и одинакова для всех инвестиционных проектов и для любого из рассматриваемых проектов степень риска одинакова. Различают простые (статические) и усложненные (динамические) методы. Простые методы традиционно использовались в социалистической экономике и отвечали действующим тогда условиям хозяйствования. В рыночных условиях используются методы, основанные на теории временной стоимости денег, которые устранили недостаток ранее действующих методик. Важнейшая задача анализа инвестиционных проектов – расчет будущих денежных потоков, возникающих при реализации проекта, но не прибыли. Анализ инвестиционных проектов основан на исследовании доходов и расходов, выраженных в форме денежных потоков, но не на изменениях, вызванных условностями бухгалтерского учета. В данной главе рассматриваются только методы и показатели эффективности инвестиций, основанные на принципе дисконтирования. При анализе потоков платежей используются обобщающие показатели: наращенная стоимость; приведенная стоимость; норма доходности. Эти показатели уже рассматривались в теоретической части, но для инвестиционных процессов они приобретают свою специфику. Чистый приведенный доход Поскольку денежные средства распределены во времени, то и здесь фактор времени играет важную роль. При оценке инвестиционных проектов используется метод расчета чистого приведенного дохода, который предусматривает дисконтирование денежных потоков: все доходы и затраты приводятся к одному моменту времени. Центральным показателем в рассматриваемом методе является показатель NPV (net present value) – текущая стоимость денежных потоков за вычетом текущей стоимости денежных оттоков. Это обобщенный конечный результат инвестиционной деятельности в абсолютном измерении. При разовой инвестиции расчет чистого приведенного дохода можно представить следующим выражением: где Rk – годовые денежные поступления в течение n лет, k = 1, 2, …, n; IC – стартовые инвестиции; i – ставка дисконтирования. Важным моментом является выбор ставки дисконтирования, которая должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке. Для определения эффективности инвестиционного проекта отдельной фирмой в качестве ставки дисконтирования используется средневзвешенная цена капитала, используемого фирмой для финансирования данного инвестиционного проекта. Последовательное инвестирование финансовых ресурсов Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение нескольких лет (m), то формула для расчета модифицируется: Показатель NPV является абсолютным приростом, поскольку оценивает, на сколько приведенный доход перекрывает приведенные затраты: при NPV > 0 проект следует принять; при NPV < 0 проект не принимается, при NPV = 0 проект не имеет ни прибыли, ни убытков. Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала фирмы в случае принятия данного проекта. Одно из важных свойств данного критерия, что показатель NPV различных проектов можно суммировать, поскольку он аддитивен во времени. Это позволяет использовать его при анализе оптимальности инвестиционного портфеля. Пример. Фирма рассматривает целесообразность инвестиционного проекта, стоимость которого составляет 210 тыс. долларов. По прогнозам ежегодные поступления составят 55 тыс. долларов. Проект рассчитан на 5 лет. Необходимая норма прибыли составляет 8%. Следует ли принять этот проект? Решение: Чистая стоимость проекта равна: 12) NPV = 55'000 (1,08)-1 + 55'000 (1,08)-2 + 55'000 (1,08)-3 + 55'000 (1,08)-4 ++ 55'000 (1,08)-5 - 210'000 = 50'926 + 42'867 + 39'692 + 36'751 + 34'029 - 210'000 == 204'265 - 210'000 = -5'735 долларов. Поскольку величина чистой текущей стоимости -5'735 долларов, т.е. NPV < 0, то проект не может быть принят. Как правило, основываются на том, что величина NPV находится на начало реализации инвестиционного проекта, однако можно определять эту величину на момент завершения процесса вложений или на иной момент времени. Напомним, что ставка дисконтирования – результат выбора, субъективного суждения. Кроме того, при высоком уровне ставки отдаленные платежи будут оказывать на величину NPV малое влияние, поэтому варианты, отличающиеся по продолжительности периодов отдачи, могут оказаться равноценными по конечному экономическому эффекту. Срок окупаемости Для анализа инвестиций применяют и такой показатель, как срок окупаемости– продолжительность времени, в течение которого дисконтированные на момент завершения инвестиций прогнозируемые денежные поступления равны сумме инвестиций. Иными словами – это сумма лет, необходимых для возмещения стартовых инвестиций: т.е. NPV = 0. Период окупаемости можно определить как ожидаемое число лет по упрощенной формуле: nок = Число лет до года окупаемости + (Не возмещенная стоимость на начало года окупаемости / Приток наличности в течение года окупаемости) Данный показатель определяет срок, в течение которого инвестиции будут "заморожены", поскольку реальный доход от инвестиционного проекта начнет поступать только по истечении периода окупаемости. Пример. Рассчитать срок окупаемости проекта, для которого размер инвестиций составляет 1 млн руб., а денежные поступления в течение 5 лет будут составлять: 200; 500; 600; 800; 900 тыс. руб. соответственно. Ставка дисконтирования 15%. Решение: Рассчитаем дисконтированный денежный поток:
Срок окупаемости проекта: kок = 3 + 54 / 458 = 3,12 Таким образом, период, реально необходимый для возмещения инвестированной сумы, составит 3,12 года или 3 года и 44 дня. Если доходы можно представить в виде аннуитета, то 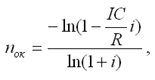 Срок окупаемости существует, если не нарушаются определенные соотношения между поступлениями и размером инвестиций. При ежегодных постоянных поступлениях это соотношение имеет вид: Rk < IC • i, т.е. не всякий уровень дохода при прочих равных условиях приводит к окупаемости инвестиций. |
