Федеральное агентство по образованию иркутский государственный технический университет

• Название: Федеральное агентство по образованию иркутский государственный технический университет
• Дата: 29.04.2023
• Размер: 7.53 Mb.
• Имя файла: mk. kurs lektsii +.doc
• Тип: Курс лекций; #1097232
• страница: 10 из 44

Рис. 3.11. Схема распределения сосредоточенной нагрузки

на стенку сварной балки при поэтажном сопряжении балок
При наличии местных напряжений σ_loc, возникающих в местах приложения сосредоточенной нагрузки к верхнему поясу при поэтажном сопряжении балок (рис. 3.11) (балки настила попадают между поперечными ребрами жесткости, укрепляющими стенку от потери устойчивости), необходима проверка прочности стенки на местные сминающие напряжения по формуле



где σ_loc = F/(l_eft_w) = 334,08 / (20,5 · 1,2) = 13,58 кН/см²,

здесь F= 2Q = 2 · 167,04 = 334,08 кН – расчетное значение сосредоточенной силы, равное двум реакциям от балок настила;

условная длина распределения сосредоточенной нагрузки на стенку главной балки;

b = 155 мм – ширина пояса балки настила;

t_f= 25 мм – толщина верхнего пояса главной балки.

Прочность балки обеспечена.

3.6.4. Изменение сечения балки по длине

Сечение составной балки, подобранное по максимальному изгибающему моменту в середине пролета, можно уменьшить в местах снижения моментов. Наибольший эффект дает симметричное изменение сечения на расстоянии x = l/6 от опор. Наиболее простым является изменение сечения за счет уменьшения ширины пояса (рис. 3.12).


Рис. 3.12. Изменение сечения балки по длине

Стыкуем сжатый и растянутый пояса прямым сварным швом с выводом концов шва на технологические подкладки с применением механизированной сварки без использования физических способов контроля качества швов. Расчетное сопротивление таких сварных соединений при растяжении принимается пониженным:

R_wy = 0,85R_y = 0,85 ∙ 23 = 19,55 кН/см².

Для снижения концентрации напряжений при сварке встык элементов разной ширины на элементе большей ширины делаем скосы с уклоном 1:5.
Определяем расчетный момент и перерезывающую силу на расстоянии от опоры:





Определяем требуемые:

– момент сопротивления измененного сечения, исходя из прочности сварного стыкового шва, работающего на растяжение:



– момент инерции измененного сечения



– момент инерции пояса



– площадь пояса



– ширину пояса



По конструктивным требованиям ширина пояса должна отвечать условиям:

–

–

–

По сортаменту принимаем измененный пояс из универсальной стали сечением 24025 мм с площадью

Вычисляем геометрические характеристики измененного сечения балки:

– момент инерции



– момент сопротивления

W₁ = 2I₁/h = 2∙1035188 / 155 = 13357 см³;

– статический момент пояса относительно оси х-х



Производим проверку прочности балки в месте изменения сечения в краевом участке стенки на уровне поясных швов (рис. 3.13) на наиболее неблагоприятное совместное действие нормальных и касательных напряжений, для чего определяем:

– нормальное напряжение



– касательное напряжение





Рис. 3.13. Распределение напряжений в месте изменения сечения балки
Проверяем прочность стенки балки по формуле



где 1,15– коэффициент, учитывающий локальное развитие пластических де-

формаций в стенке балки.

В случае невыполнения условия необходимо увеличить толщину стенки t_w.

При наличии местной нагрузки F_b (см. рис. 3.11) и отсутствия поперечного ребра жесткости в рассматриваемом сечении проверка прочности стенки производится с учетом локальных напряжений σ_loc по формуле



Если эта проверка не выполняется, то стенку балки под сосредоточенной нагрузкой можно укрепить поперечным ребром жесткости. Это ребро через пригнанный торец воспримет сосредоточенное давление и через сварные швы, соединяющие ребро со стенкой, распределит его на всю высоту стенки. При наличии таких ребер стенка балки с учетом действия местных напряжений на прочность не проверяется.

3.6.5. Проверка общей устойчивости балки

Общая устойчивость балки считается обеспеченной при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный, а также, если соблюдается условие: отношение расчетной длины участка балки l_ef между связями, препятствующими поперечным смещениям сжатого пояса балки, к его ширине b_f не превышает критическое значение, определяемое по формуле



где l_ef = 3 м – расстояние между точками закрепления сжатого пояса от поперечных смещений, равное шагу балок настила a₁.

Проверяем:

– в середине пролета балки



– в измененном сечении балки



Общая устойчивость балки обеспечена.

В случае невыполнения условий необходимо проверить устойчивость балки по формуле



где φ_b– коэффициент устойчивости при изгибе, определяемый по [6, прил.7*];

W_c – момент сопротивления сечения относительно оси x-x, вычисленный для сжатого пояса;

_с = 0,95 – коэффициент условий работы при расчетах на общую устойчивость при _b  1 (см. табл. 1.3).

3.6.6. Проверка местной устойчивости элементов балки

Проверка местной устойчивости сжатого пояса не требуется, так как она была обеспечена надлежащим назначением отношения свеса пояса к толщине (см. п. 3.6.2).

Проверка местной устойчивости стенки балки. Под действием нормальных и касательных напряжений стенка балки может потерять местную устойчивость, т.е. может произойти ее местное выпучивание. Это произойдет в том случае, если действующие в балке отдельные виды напряжений или их совместное воздействие превысят критические напряжения потери устойчивости. Устойчивость стенки обычно обеспечивают не за счет увеличения ее толщины, что привело бы к повышенному перерасходу материала из-за большого размера стенки, а за счет укрепления ее ребрами жесткости.

Стенку балки следует укреплять поперечными ребрами жесткости, если значение условной гибкости превышает 3,2 при отсутствии местной нагрузки на пояс балки и 2,2 – при наличии местной нагрузки.

Определяем условную гибкость стенки:



следовательно, поперечные ребра жесткости необходимы (рис. 3.14). Расстояние между основными поперечными ребрами a не должно превышать 2h_w при _w > 3,2 и 2,5h_w при _w 3,2. Для балок, рассчитываемых в упругой стадии, допускается превышать указанные выше расстояния между ребрами до значения 3h_w при условии передачи нагрузки через сплошной жесткий настил или при значении гибкости сжатого пояса балки λ_b = l_ef /b_f, не превышающем ее предельного значения λ_ub (в рассматриваемом примере это условие соблюдается: в середине пролета балки λ_b = 6,67< λ_ub = 15,64 и в измененном сечении λ_b = 12,56< λ_ub = 14,3), и при обязательном обеспечении местной устойчивости элементов балки.



Рис. 3.14. Схема балки, укрепленной поперечными ребрами жесткости

Расстояние между ребрами назначаем , что увязывается с шагом балок настила При шаге а = 3 м поперечное ребро жесткости попадает на монтажный стык в середине пролета балки, поэтому первое и последующие за ним ребра смещаем к опоре на расстояние а/2 = 1,5м.

Ширина выступающей части парного ребра должна быть не менее

b_r = h_w/30 + 40 = 1500 / 30 + 40 = 90 мм.

для одностороннего – b_r = h_w/24 + 50 = 1500 / 24 + 50 = 112,5 мм.

Толщина ребра



Принимаем ребро жесткости по ГОСТ 103–76* (табл. 3.7) из двух стальных полос 907 мм. Ребра жесткости привариваются к стенке непрерывными угловыми швами минимальной толщины. Торцы ребер должны иметь скосы с размерами не менее 4040 мм для снижения концентрации сварочных напряжений в зоне пересечения сварных швов и пропуска поясных швов балки.

Поперечное ребро жесткости, расположенное в месте приложения сосредоточенной нагрузки F_b = 334,08 кН к верхнему поясу балки проверяют расчетом на устойчивость: двустороннее ребро – как центрально-сжатую стойку, одностороннее – как стойку, сжатую с эксцентриситетом, равным расстоянию от срединной плоскости стенки до центра тяжести расчетного сечения стойки. При этом в расчетное сечение стойки включают сечение ребра жесткости и устойчивые полосы стенки шириной

c = 0,65t_w = 0,65 · 1,2 = 22,85 см

с каждой стороны ребра, а расчетную длину принимают равной высоте стенки h_w = 1500 мм (рис. 3.15).



Рис. 3.15. Расчетное сечение условной стойки

Расчетная площадь стойки при двустороннем ребре

A_s= (2b_r+ t_w)t_r+ 2ct_w = (2 · 9 + 1,2) 0,7 + 2 ∙ 22,85 ∙ 1,2) = 68,28 см².

Момент инерции сечения стойки

I_z = t_r³/12 + 2ct_w³/12 = 0,7 (2 ∙ 9 +1,2)³ / 12 + 2 ∙ 22,85 ∙ 1,2³ / 12 = 412,88 см⁴.

Радиус инерции

i_z = = = 2,46 см.

Гибкость стойки

λ_z = l_ef /i_z = 150 / 2,46 = 60,98.

Условная гибкость



Производим проверку устойчивости стойки: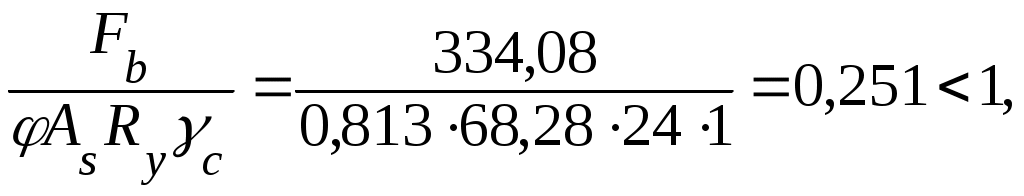



где φ = 0,813 – коэффициент устойчивости при центральном сжатии, принимаемый по табл. 3.11 в зависимости от условной гибкости λ_z для типа кривой устойчивости ^״b^״; тип кривой устойчивости зависит от формы сечений и толщины проката (табл. 3.12), при условной гибкости λ_z ≤ 0,4 коэффициент φ принимается равным единице.

Условие выполняется.

Таблица 3.11

Коэффициенты устойчивости при центральном сжатии

Условная гибкость	Коэффициент  для типов кривых устойчивости			Условная гибкость	Коэффициент  для типов кривых устойчивости
	a	b	c		a	b	c
0,4	999	998	992	3,2	660	602	526
0,6	994	986	950	3,4	615	562	492
0,8	981	967	929	3,6	572	524	460
1,0	968	948	901	3,8	530	487	430
1,2	954	927	878	4,0	475	453	401
1,4	938	905	842	4,2	431	421	375
1,6	920	881	811	4,4	393	392	351
1,8	900	855	778	4,6	359	359	328
2,0	877	826	744	4,8	330	330	308
2,2	851	794	709	5,0	304	304	289
2,4	820	760	672	5,2	281	281	271
2,6	785	722	635	5,4	261	261	255
2,8	747	683	598	5,6	242	242	240
3,0	704	643	562	5,8	226	226	226

П р и м е ч а н и е. Значения коэффициента  в таблице увеличены в 1000 раз.

Устойчивость стенок балок не требуется проверять, если условная гибкость стенки _w не превышает значений:

3,5 – для балок с двухсторонними поясными швами при отсутствии местной нагрузки на пояс балки;

3,2 – для таких же балок с односторонними поясными швами;

2,5 – для балок с двухсторонними поясными швами при наличии местной нагрузки на пояс.

Таблица 3.12