Федеральное агентство по образованию иркутский государственный технический университет
 Скачать 7.53 Mb.
|
|
Характеристики кривых устойчивости
В нашем примере  следовательно, требуется проверка стенки на местную устойчивость.Расчет на устойчивость стенки балки симметричного сечения, укрепленной только поперечными основными ребрами жесткости, при отсутствии местных напряжений смятия  и условной гибкости стенки  выполняется по формуле при наличии местного напряжения (см. рис. 3.11) – по формуле  где σ,и σloc – действующие нормальные, касательные и локальные напряжения в месте соединения стенки с поясом от средних значений M,Q и Fb в пределах отсека; если длина отсека больше его расчетной высоты (a> hw), то M и Q определяются для наиболее напряженного участка отсека с длиной, равной высоте отсека hw; если в пределах отсека MиQменяют знак, то их средние значения следует вычислять на участке отсека с одним знаком; σсr , σloc,сr, τсr – критические напряжения, определяемые по СНиП [6]. Проверку местной устойчивости стенки производят в наиболее нагруженных отсеках: первом от опоры; среднем и, при наличии изменения сечения балки по длине, в отсеке с измененным сечением. Проверка местной устойчивости стенки в среднем отсеке балки (рис. 3.16).  Рис. 3.16. Распределение изгибающих моментов и поперечных сил в среднем отсеке Так как а = 3 м > hw = 1,5 м, определяем Mср и Qср по середине условного отсека шириной, равной половине высоты стенки hw, для чего вычисляем величины моментов и поперечных сил на границах расчетного участка (х1 = 7,5 м; х2 = 9 м): M1 = qx1(l – x1)/2 = 115,03 · 7,5 (18 – 7,5) / 2 = 4529,31 кН∙м; M2 = Mmax = 4658,72 кН∙м;  Q2 = 0;Mср = (M1 + M2)/2 = (4529,31 + 4658,72) / 2 = 4594,02 кН·м; Qср = (Q1 + Q2)/2 = 172,55 / 2 = 86,28 кН. Краевое напряжение сжатия в стенке σ = Mср(hw/h)/Wx = 4594,02 (150 / 155) /21234 = 20,09 кН/см2. Среднее касательное напряжение в отсеке τ = Qср/(hwtw) = 86,28 / (150 ∙ 1,2) = 0,48 кН/см2. Локальное напряжение σloc= 0. Критическое нормальное напряжение  где cсr = 33,4 – коэффициент, определяемый по табл. 3.13 в зависимости от значения коэффициента δ, учитывающего степень упругого защемления стенки в поясах,  здесь β = ∞ – при непрерывном опирании плит; β = 0,8 – в прочих случаях. Таблица 3.13 Значения коэффициента ссr в зависимости от значения δ
Критическое касательное напряжение определяется по формуле  где  – отношение большей стороны отсека a или hw к меньшей d; здесь d = hw = 1,5 м < a = 3 м. Проверяем местную устойчивость стенки:  Устойчивость стенки в середине балки обеспечена. Проверка местной устойчивости стенки в месте изменения сечения балки на расстоянии х = 3 м от опоры. Расчетные усилия равны: М1 = 2588,18 кН·м; Q1 = 690,18 кН. Краевое напряжение сжатия в стенке σ = M1(hw/h)/W1 = 258818 (150 / 155) /13357 = 18,75 кН/см2. Среднее касательное напряжение в отсеке τ = Q1/(hwtw) = 690,18 / (150 ∙ 1,2) = 3,83 кН/см2. Локальное напряжение σloc= 0. Критическое нормальное напряжение  где cсr = 31,8 – по табл. 3.13 в зависимости от  Критическое касательное напряжение  (см. проверку местной устойчивости стенки в среднем отсеке).Производим проверку:  Стенка в отсеке балки с измененным сечением устойчива. Проверка местной устойчивости стенки в первом отсеке в сечении на расстоянии от опоры x1 = a1/2 = 1,5 / 2 = 0,75 м (рис. 3.17), где a1= hw= 1,5 м.  Рис. 3.17. К проверке местной устойчивости стенки балки у опоры Определяем усилия: M1 = qx1(l – x1)/2 = 115,03 · 0,75 (18 – 0,75) / 2 = 744,1 кН∙м;  Краевое напряжение сжатия в стенке σ = M1(hw/h)/W1 = 74410 (150 / 155) /13357 = 5,39 кН/см2. Среднее касательное напряжение в отсеке τ = Q1/(hwtw) = 949 / (150 ∙ 1,2) = 5,27 кН/см2. Локальное напряжение  Критическое нормальное напряжение  при = 1,16.Критическое касательное напряжение определяется по формуле  где  ; здесь d = hw = a1 = 1,5 м – меньшая из сторон отсека. Производим проверку:  Стенка в первом от опоры отсеке устойчива. В случае невыполнения условий устойчивости стенки необходимо увеличить толщину стенки tw или уменьшить расстояние между поперечными ребрами жесткости а, затем повторно произвести проверку ее устойчивости. Проверка местной устойчивости стенки балки при наличии местных напряжений (σloc 0). При наличии местных напряжений проверку стенки на местную устойчивость следует выполнять в зависимости от значения a/hw, при этом значения M иQ определяют в одном сечении балки. Значения критических напряжений определяются в предположении выпучивания стенки между ребрами жесткости при ее потере устойчивости по одной полуволне при частом расположении ребер (a/hw 0,8) и при более редкой расстановке ребер жесткости (a/hw > 0,8) – по одной или двум полуволнам. Значение критического нормального напряжения σcr при a/hw 0,8 определяется так же, как и при отсутствии местных напряжений по формуле 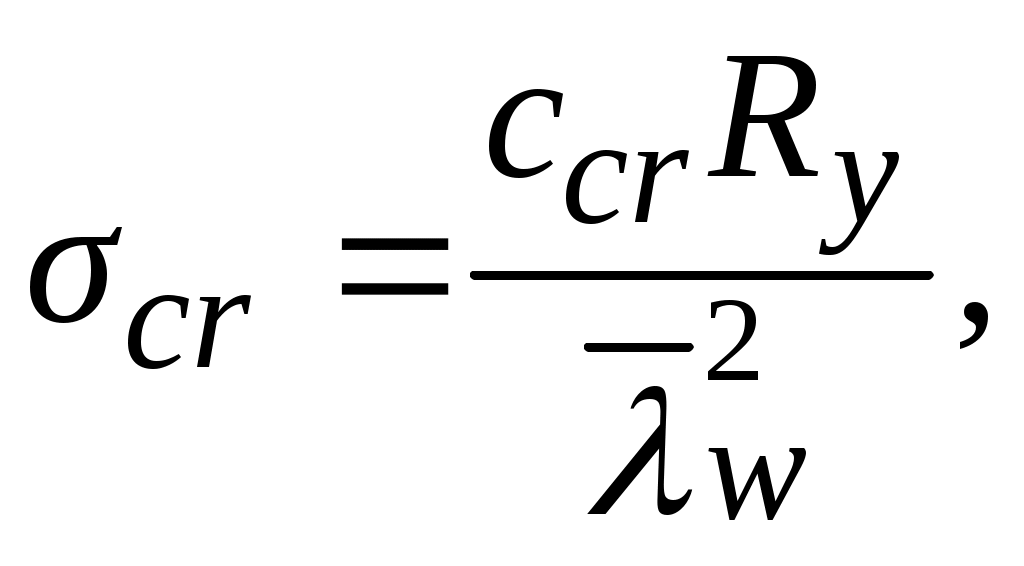 где ccr находится по табл. 3.13; Критическое напряжение потери устойчивости от действия местных напряжений определяется по формуле 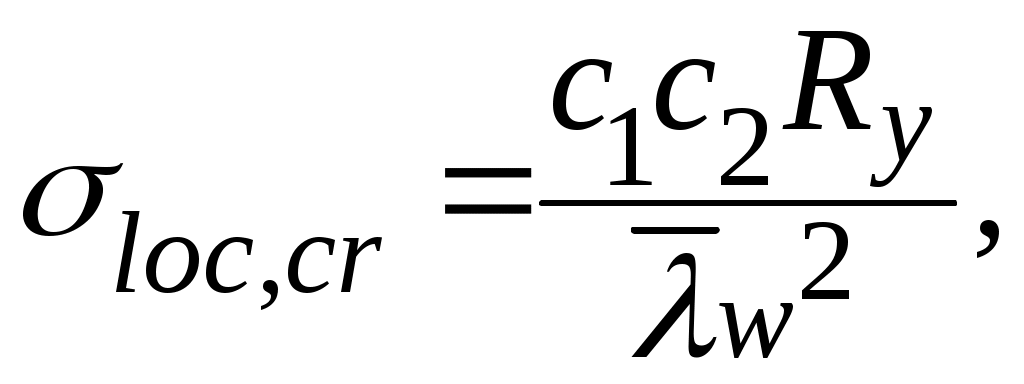 где с1 – коэффициент, принимаемый по табл. 3.14 в зависимости от a/hw – соотношения сторон проверяемой пластины и значения, ρ = 1,04lef /hw – относительной длины загружения пластины местной нагрузкой lef к высоте стенки hw (см. рис. 3.11), здесь lef = b + 2tf ; с2 – коэффициент, принимаемый по табл. 3.15 в зависимости от отношенияa/hw и значения δ. Таблица 3.14 Значения коэффициента c1
Таблица 3.15 Значения коэффициента c2
При отношении a/hw> 0,8 рассматривают два случая проверки устойчивости стенки: В первом случае вычисляются критическое нормальное σcr и локальное σloc,cr напряжения по следующим формулам: 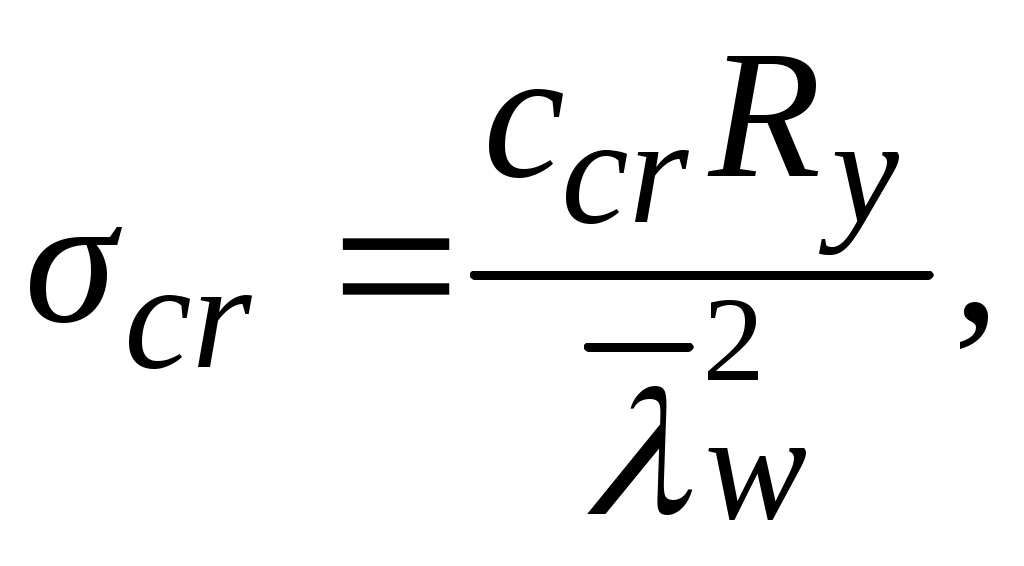 где ccr определяется по табл. 3.13;  где для его вычисления при определении коэффициентов c1 и c2 по табл. 3.14 и 3.15 вместо a необходимо принять a1 = 0,5aпри0,8 ≤ a/hw ≤ 1,33 и a1 = 0,67hwпри a/hw > 1,33. Во втором случае их определяют так: – критическое нормальное напряжение 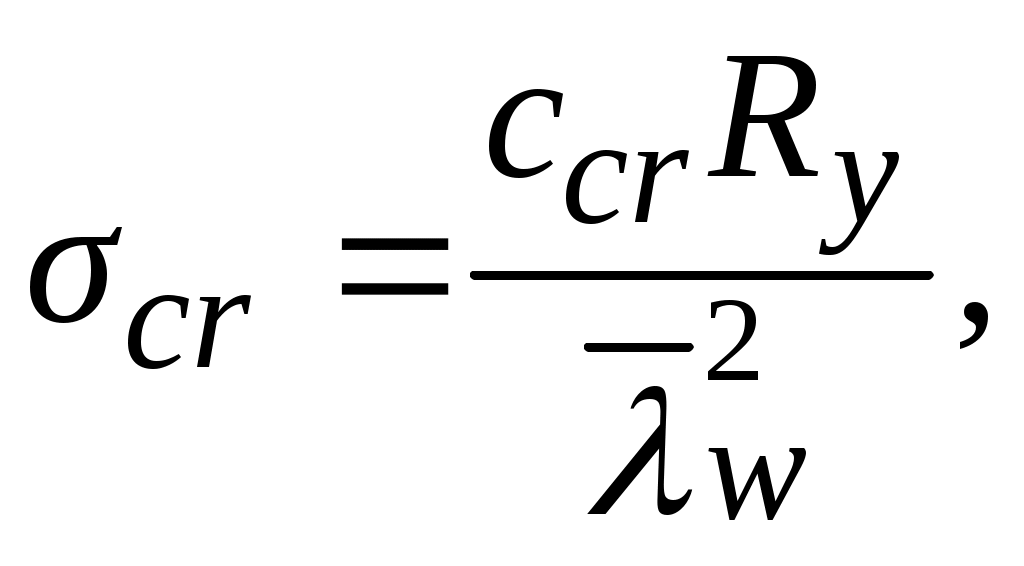где ccr определяется по табл. 3.16; – критическое локальное напряжение потери устойчивости  где коэффициенты c1 и c2 определяют по фактическому отношению сторонa/hw(если a/hw> 2, в расчете принимаютa/hw= 2). Таблица 3.16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
