Федеральное агентство по образованию иркутский государственный технический университет

• Название: Федеральное агентство по образованию иркутский государственный технический университет
• Дата: 29.04.2023
• Размер: 7.53 Mb.
• Имя файла: mk. kurs lektsii +.doc
• Тип: Курс лекций; #1097232
• страница: 14 из 44

Предельные условные гибкости

Относительный эксцентриситет	Сечение элемента	Значения  и1	Формулы для определения
m = 0	Двутавровое	 < 2,0   2,0	но не более 2,3
	Коробчатое, швеллерное прокатное	 < 1,0   1,0	но не более 1,6
	Швеллерное, кроме прокатного	 < 0,8   0,8	но не более 1,6
m  1,0	Двутавровое, коробчатое	 < 2,0   2,0	но не более 3,1

Обозначения:

 – условная гибкость элемента, принимаемая в расчете на устойчивость при центральном сжатии;

₁ – условная гибкость элемента, принимаемая в расчете на устойчивость в плоскости действия момента.

П р и м е ч а н и я: 1. К коробчатым относятся замкнутые прямоугольные профили (составные, гнутые прямоугольные и квадратные).

2. В коробчатом сечении при m > 0 значение _uw следует определять для стенки, параллельной плоскости изгибающего момента.

3. При значениях 0 < m < 1,0 значение _uw следует определять линейной интерполяцией между значениями, вычисленными при m= 0 и m= 1,0.

Отношение ширины свеса полки b_ef = (b_f – t_w)/2 = (40 – 8) / 2 = 19,6 см

к толщине полки t_f в центрально-сжатых элементах с условной гибкостью

 = 0,8 – 4 по условию местной устойчивости полки не должно превышать



откуда определяем минимальную толщину полки:



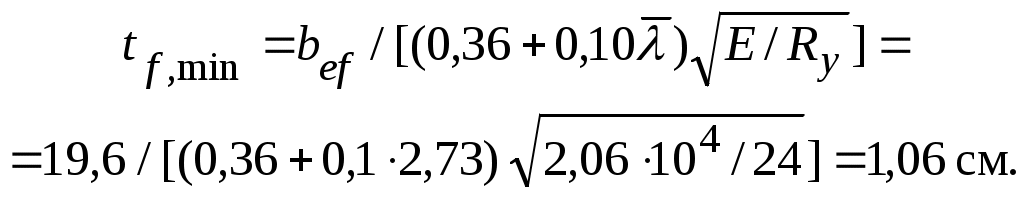
Требуемая площадь одной полки





Рис. 4.4. Укрепление стенки продольными и

поперечными ребрами жесткости

Требуемая толщина полки



Принимаем

Высота сечения

h = h_w + 2t_f = 400 + 2 ∙ 1,2 = 42,4 см.

Площадь полки



Вычисляем геометрические характеристики сечения:

– площадь



– момент инерции относительно оси у-у (моментом инерции стенки пренебрегаем)



– радиус инерции



– фактическую гибкость



– условную гибкость



– коэффициент устойчивости при центральном сжатии

Проверяем общую устойчивость колонны относительно оси y-y:



где _с = 1 – коэффициент условий работы по табл. 1.3.

Недонапряжение в колонне



что допустимо в составном сечении согласно СНиП [6].

Сечение принято.

В случае невыполнения условия устойчивости колонны, производится корректировка размеров сечения и повторная проверка. Корректировка, как правило, производится за счет изменения размеров полок при обязательном соблюдении условия их местной устойчивости.

Для укрепления контура сечения и стенки колонны при устанавливают поперечные ребра жесткости, расположенные на расстоянии a= (2,5...3)h_w одно от другого; на каждом отправочном элементе должно быть не менее двух ребер (см. рис. 4.4). Минимальные размеры выступающей части b_r и толщины t_r поперечных ребер жесткости принимаются так же, как в главной балке.

Проверяем:

,

постановка поперечных ребер жесткости не требуется.

В местах примыкания к колонне связей, балок, распорок и других элементов ребра жесткости устанавливают в зоне передачи сосредоточенных усилий независимо от толщины стенки.

Соединение пояса со стенкой рассчитывают на сдвиг по формуле



где T = Q_ficS_f/I – сдвигающее пояс усилие на единицу длины, вызываемое

условной поперечной силой

Q_fic = 7,15 ∙ 10^–6(2330 – E/R_y)N/φ,

здесь φ – коэффициент устойчивости при центральном сжатии, принимаемый при расчете по условной гибкости колонны относительно оси x-x;

S_f – статический момент пояса колонны относительно оси x-x;

I_x – момент инерции сечения колонны.

В центрально-сжатых колоннах сдвигающее усилие незначительно, так как поперечная сила, возникающая от случайных воздействий, невелика. Соединение стенки с полками производится автоматической сваркой. Минимальный катет сварного шва принимается конструктивно в зависимости от максимальной толщины свариваемых элементов (t_max = t_f= 12 мм) k_f = 5 мм.

4.3. Расчет и конструирование сквозной колонны

Пример 4.3. Подобрать сквозную колонну из двух швеллеров, соединенных планками (рис. 4.5), по данным примера 4.2.



Рис. 4.5. Составной стержень колонны на планках

Расчетом сквозных колонн относительно материальной оси x-x определяют номер профиля, а расчетом относительно свободной оси y-y, производимым так же, как сплошных колонн, но с заменой гибкости стержня приведенной гибкостью, назначают расстояние между ветвями, при котором обеспечивается равноустойчивость стержня в двух взаимно перпендикулярных плоскостях.

4.3.1. Расчет колонны на устойчивость относительно

материальной оси x-x

Рекомендуют предварительно задаться гибкостью: для средних по длине колонн 5 – 7 м с расчетной нагрузкой до 2500 кН принимают гибкость = 90 – 50; с нагрузкой 2500 – 3000 кН – = 50 – 30, для более высоких колонн необходимо задаваться гибкостью несколько большей.

Предельная гибкость колонн где – коэффициент, учитывающий неполное использование несущей способности колонны, принимаемый не менее 0,5. При полном использовании несущей способности колонны _u = 120.

Задаемся гибкостью = 50.

Условная гибкость



По табл. 3.12 определяем тип кривой в соответствии с типом принятого сечения (тип ′′b′′). Согласно табл. 3.11 условной гибкости = 1,7соответствует коэффициент устойчивости при центральном сжатии = 0,868.

Находим требуемую площадь поперечного сечения по формуле

.

Требуемая площадь одной ветви



Требуемый радиус инерции относительно оси x-x



По требуемым площади A_b и радиусу инерции i_x выбираем из сортамента (ГОСТ 8240-93) два швеллера №36, имеющих следующие характеристики сечения:

A_b = 53,4 см²; A = 2A_b = 53,4  2 = 106,8 см²; I_x = 10820 см⁴; I₁= 513 см⁴;

i_x= 14,2 см; i₁= 3,1 см; толщину стенки d= 7,5 мм; ширину полки b_b= 110 мм; привязку к центру тяжести z_о = 2,68 см; линейную плотность (массу 1 м пог.) 41,9 кг/м.

Если максимальный швеллерный профиль [40 не обеспечивает требуемую несущую способность сквозной колонны, переходят на проектирование

ветвей колонны из прокатных двутавров, принимаемых по ГОСТ 8239–89.

Определяем:

– гибкость колонны

;

– условную гибкость



– для кривой устойчивости ′′b′′ коэффициент устойчивости φ = 0,833. Проверяем общую устойчивость колонны относительно материальной

оси x-x:



Общая устойчивость колонны обеспечена.

Недонапряжение в колонне



Если устойчивость колонны не обеспечена или получен большой запас, то изменяют номер профиля и вновь делают проверку.
4.3.2. Расчет колонны на устойчивость относительно свободной оси y-y

Расчет на устойчивость центрально-сжатой колонны сквозного сечения, ветви которой соединены планками или решетками, относительно свободной оси (перпендикулярной плоскости планок или решеток) производят по приведенной гибкости _ef :

– для колонны с планками

при

и при

– для колонны с треугольной решеткой



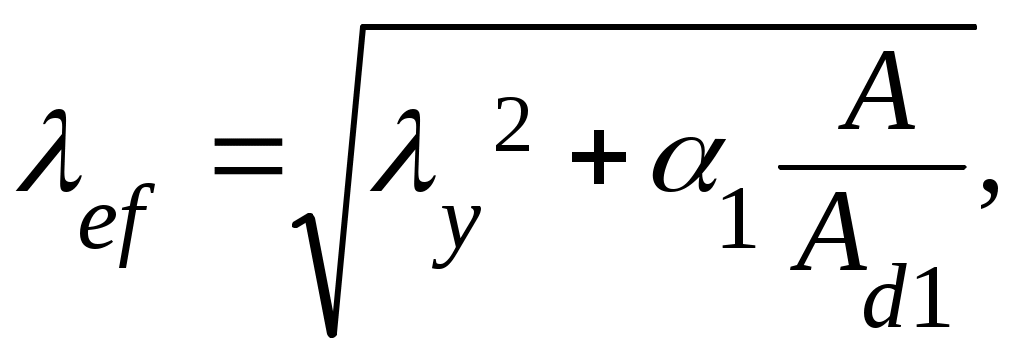
где – теоретическая гибкость стержня колонны относительно оси y-y;

– гибкость ветви колонны относительно оси 1-1;

– момент инерции сечения одной планки относительно собственной оси z-z;

I₁ – момент инерции ветви относительно оси 1-1 (по сортаменту);

l_b – расстояние между планками по центрам тяжести;

l_ob– расстояние между планками в свету;

b_o– расстояние между центрами тяжести ветвей колонн;

– отношение погонных жесткостей ветви и планки;

A – площадь сечения всего стержня колонны;

A_d1 – суммарная площадь поперечных сечений раскосов решеток, лежащих в плоскостях, перпендикулярных оси у-у;

α₁ = 10a³/(b²l) – коэффициент, зависящий от угла наклона раскоса к ветви β (a,b,l – размеры, определяемые по рис. 4.6).


Рис. 4.6. Схема треугольной решетки

Подбор сечения колонн относительно оси y-y производится из условия ее равноустойчивости (равенства гибкости λ_xотносительно x-xи приведенной гибкости λ_efотносительно оси y-y),которая достигается за счет изменения расстояния между ветвями b_o.

4.3.3. Сквозная колонна с планками

Расчет колонны относительно свободной оси y-y. Приравнивая находим требуемое значение гибкости относительно свободной оси:



где ₁ = 33 – предварительно принятая гибкость ветви (гибкость ветви назначают в пределах ₁ = 30 – 40 и обеспечивают ее при последующем конструировании колонны путем выбора соответствующего расстояния между планками l_o = λ₁i₁).

По λ_y находим радиус инерции:



Воспользовавшись приближенными значениями радиусов инерции, приведенными в табл. 4.1, определяем ширину сечения:

b =i_y/0,44 = 17,38 / 0,44 = 39,5 см.

Принимаем b= 400 мм и определяем расстояние между ветвями:



Проверяем расстояние в свету между полками швеллеров:

_{а = b – 2bb= 400 – 2 · 110 = 180 мм > 100 мм.}

Расстояние между ветвями увеличивать не требуется.

Проверка колонны на устойчивость относительно оси у-у. До проверки устойчивости колонны нужно скомпоновать сечение стержня, установить расстояние между планками, назначить их размеры.

Расчетная длина ветви



Принимаем расстояние в свету между планками l_ob= 100 см.

Длину планки b_пл принимают равной расстоянию в свету между ветвями с напуском на ветви по 20…30 мм:



Высоту планок h_пл обычно устанавливают в пределах (0,5 – 0,75)b =

= 200 – 300 мм, где b= 400 мм – ширина колонны. Принимаем h_пл = 240 мм.

Толщину планок принимают t_nл = 6 – 12 мм и по условиям местной устойчивости она должна быть:



.

Окончательно принимаем планки из листов 2402408 мм.

Момент инерции стержня колонны относительно оси у-у



Радиус инерции

i_y = см.

Гибкость стержня колонны

λ_y = l_y/i_y = 813 / 17,6 = 46,19.

Для вычисления приведенной гибкости λ_efотносительно свободной оси проверяется отношение погонных жесткостей планки и ветви:



где



Гибкость ветви колонны



Приведенная гибкость



Условная приведенная гибкость



По табл. 3.11 в зависимости от для типа кривой устойчивости ″b″ находим коэффициент устойчивости при центральном сжатии  = 0,833.

Производим проверку:



Устойчивость колонны обеспечена.

Недонапряжение в колонне



Сечение принято.

Расчет планок.

Проверяем принятое сечение планок. Расчет соединительных элементов (планок, решетки) сжатых составных стержней выполняется на условную поперечную силу Q_fic, принимаемую постоянной по всей длине стержня колонны и определяемую по формуле

Q_fic = 7,15·10^-6 (2330 – E/R_y)N/φ =

= 7,15·10^-6(2330 – 2,06 · 10⁴ / 24) 2067,18 / 0,833 = 26,3 кН,

где = 0,833 – коэффициент устойчивости при сжатии, принимаемый для составного стержня в плоскости соединительных элементов.

Поперечная сила, приходящаяся на планку одной грани (рис. 4.7) вычисляется по формуле



Сдвигающая сила в месте прикрепления планки к ветви колонны