Лабораторные фх. Лабник по ф и к химии. Физическая и коллоидная химия сборник лабораторных работ СанктПетербург 2008 удк 541 076 (075. 83) Физическая и коллоидная химия. Сборник лабораторных работ

• Название: Физическая и коллоидная химия сборник лабораторных работ СанктПетербург 2008 удк 541 076 (075. 83) Физическая и коллоидная химия. Сборник лабораторных работ
• Анкор: Лабораторные фх
• Дата: 23.06.2022
• Размер: 4.14 Mb.
• Имя файла: Лабник по ф и к химии.doc
• Тип: Сборник; #612950
• страница: 27 из 38

Молекулярная адсорбция

При молекулярной адсорбции (физической, ван-дер-ваальсовой) адсорбционные силы имеют ту же природу, что и межмолекулярные, или ван-дер-ваальсовы, силы. Физическая адсорбция всегда обратима.

Процесс молекулярной адсорбции происходит вследствие стремления системы к самопроизвольному понижению поверхностного натяжения. При перераспределении компонентов между поверхностным слоем и объемной фазой в поверхностный слой предпочтительнее переходит тот компонент, который сильнее снижает поверхностное натяжение.

Адсорбция на поверхности раздела жидкость – газ

Для интерпретаций явлений адсорбции на границе раствор — газ весьма существенно установить связь между избытком адсорбированного вещества в поверхностном слое Г, концентрацией поверхностно-активного вещества в растворе с и поверхностным натяжением а на границе раствор — газ. Эта связь для разбавленных растворов дается известным уравнением адсорбции Гиббса, выведенным им в 1876 г.:

для разбавленных растворов

для концентрированных растворов.

Уравнение адсорбции Гиббса устанавливает взаимосвязь адсорбции с концентрацией вещества в растворе и его поверхностной активностью. Поверхностная активность вещества, а значит, и адсорбция зависит от ряда факторов.

1. Природы вещества: ПАВ будут накапливаться в поверхностном слое (положительная адсорбция); поверхностно-инактивные вещества, наоборот, удаляться из поверхностного слоя (отрицательная адсорбция), если вещество не влияет на поверхностное натяжение, то адсорбции не наблюдается.

2. Полярности молекулы: уменьшение полярности молекулы приводит к росту поверхностной активности, а следовательно, к увеличению адсорбции.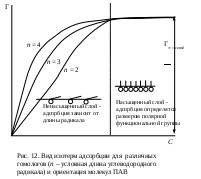


3. Строения молекулы: для членов одного гомологического ряда увеличение длины углеводородного радикала на одно звено (−СН₂−) приводит к увеличению поверхностной активности водных растворов этих веществ в 3 – 3,5 раза, при этом величина предельной адсорбции остается постоянной (эмпирическое правило Дюкло-Траубе). Математически правило Дюкло-Траубе может быть записано в виде следующего уравнения:

.

Правило Дюкло-Траубе объясняется определенной ориентацией молекул ПАВ в поверхностном слое (И. Ленгмюр, 1915 г.). При адсорбции полярная группа втягивается в полярный растворитель, например, в воду, а неполярный радикал выталкивается в неполярную фазу, например, в воздух (см. рис. 12). Происходящее при этом уменьшение поверхностной энергии ограничивает толщину поверхностного слоя размером с молекулу адсорбтива. Из-за вертикальной ориентации молекул ПАВ в поверхностном слое максимальная адсорбция Г_∞ не зависит от длины углеводородного радикала, а определяется только размерами поперечного сечения молекулы, которые в данном гомологическом ряду не меняются.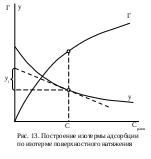



Пользуясь уравнением Гиббса, по изотерме поверхностного натяжения для поверхностно-активного вещества легко построить соответствующую изотерму адсорбции следующим образом. Возьмем какую-нибудь точку на изотерме поверхностного натяжения и проведем через нее касательную и прямые, параллельные осям координат, как это показано на рис. 13. Отрезок, отсекаемый на оси ординат касательной и прямой, параллельной оси концентраций, деленный на отрезок абсциссы, отсекаемый на ней прямой,

проведенной через точку параллельно оси ординат, равен −C(dσ/dC), т. е.

.

Подставив значение, найденное для −dσ/dC, в уравнение Гиббса, получим:

.

Определив для ряда точек изотермы поверхностного натяжения соответствующие значения величины Г, легко построить изотерму адсорбции.

Кроме того, для нахождения производной d/dC можно воспользоваться эмпирическим уравнением Б.А. Шишковского, полученным им в 1908 г.

,

где σ₀ и σ_i – поверхностное натяжение чистого растворителя и раствора соответственно; a и b – эмпирические константы.

Уравнение Шишковского хорошо применимо для вычисления поверхностного натяжения жирных кислот с не слишком большим числом атомов углерода в молекуле (до С₈).

Из уравнения Шишковского следует, что

.

После подстановки в уравнение изотермы адсорбции Гиббса получим:

.

Теоретическое обоснование эмпирическое уравнение Б.А. Шишковского получило в рамках теории мономолекулярной адсорбции И. Ленгмюра (1917 г.), основные положения которой приведены ниже.

=При адсорбции образуется насыщенный мономолекулярный слой адсорбированного вещества.

=Адсорбция является квазихимическим процессом взаимодействия между адсорбатом и адсорбентом, который можно описать с помощью величин, характеризующих химическую реакцию (тепловой эффект, энергия Гиббса, константа скорости процесса и т. п.), но при этом превращение веществ отсутствует.

=При адсорбции молекулы не могут перемещаться по поверхности, т.е. она локализована.

=Адсорбированные молекулы не взаимодействуют друг с другом.

Уравнение адсорбции Ленгмюра имеет вид:

.

Тогда константа а уравнения Шишковского связана с величиной предельной адсорбции: а = Г_∞RT; постоянная b имеет физический смысл константы равновесия процесса адсорбции.

По величине Г_∞ можно рассчитать размеры молекул ПАВ:

площадь поперечного сечения ,

где N_A – число Авогадро;

длину молекулы ,

где М_ПАВ – молярная масса ПАВ, d_ПАВ – плотность раствора ПАВ.

Адсорбция на поверхности твердого тела

Адсорбция на твердом носителе имеет ряд особенностей, отличающих этот процесс от адсорбции на поверхности раздела фаз газ – жидкость.

1. Неоднородность твердой поверхности.

2. Адсорбция проходит не на всей поверхности, а на так называемых активных центрах, которые характеризуются ненасыщенностью связей.

3. Адсорбцию на твердой поверхности можно представить как обратимый квазихимический процесс.

4. Молекула вещества считается адсорбированной, если она находится в поверхностном слое в течение определенного времени, называемого временем адсорбции (обычно 10⁻¹² – 10⁻⁵ с.).

5. Процессы адсорбции являются экзотермическими, поэтому с ростом температуры интенсивность адсорбции снижается.

6. Большинство применяемых сорбентов – это высокопористые тела с исключительно развитой поверхностью, достигающей сотни и тысячи м²/г. Адсорбенты поглощают тем больше вещества из объемной фазы, чем больше развита их поверхность. Поэтому адсорбирующую способность адсорбентов принято оценивать по их удельной поверхности, т.е. площади единицы массы адсорбента.

7. Частицы адсорбируемого вещества при адсорбции насыщают некоторую часть неуравновешенных частиц и, следовательно, понижают поверхностное натяжение. Поскольку при этом свободная энергия системы уменьшается, все адсорбционные процессы протекают самопроизвольно.

8. Если на поверхности адсорбента сорбируется только один слой молекул адсорбата, то адсорбция является мономолекулярной; при адсорбции большего числа слоев на поверхности – полимолекулярной.

9. При сорбции вещества из раствора необходимо учитывать, что последний является сложной многокомпонентной системой. При этом каждый компонент раствора теоретически способен взаимодействовать с сорбентом. Чем хуже сорбируется один компонент, тем лучше происходит адсорбция другого.

10. Количественной мерой адсорбции является избыточное (по сравнению с объемным) содержание компонента, измеряемое обычно в молях на квадратный метр поверхностного слоя сорбента:

,

где n_s – количество сорбированного вещества; s – удельная поверхность сорбента, т.е. поверхность единицы массы сорбента.

Для экспериментального исследования адсорбции на твердой поверхности применяют статический и динамический методы.

Статические методы определения адсорбции из растворов сводятся к определению концентрации исходных растворов С₀, встряхиванию навески адсорбента m_s в каждом растворе в течение времени, необходимого для установления адсорбционного равновесия, фильтрованию и определению равновесной концентрации растворенного вещества в фильтратах. Удельная адсорбция растворенного вещества

,

где С₀ и С^* – соответственно исходная и равновесная концентрации сорбируемого вещества; V – объем раствора; m_s – масса адсорбента.

В этом случае удельная адсорбция представляет собой количество вещества, сорбированное площадью поверхности 1 кг сорбента.

К числу динамических относится, например, фронтальный хроматографический метод, при котором раствор фильтруется через слой адсорбента, помещенного в колонку. В процессе сорбции отбираются пробы раствора, протекающего через колонку. При отборе проб, как правило, ориентируются на определенный объем раствора, пропущенного через сорбент. Например, пробы отбирают через 10 мл или через 50 мл. Процесс ведут до полного насыщения сорбента адсорбируемым веществом. По данным анализа строят так называемую выходную кривую в координатах концентрация раствора – объем фильтрата (см. рис. 14). Количество сорбированного вещества рассчитывают по формуле:

.

Изотерма адсорбции на твердой поверхности имеет вид, показанный на рис. 11. Удельная адсорбция увеличивается с ростом концентрации раствора. Для очень разбавленных растворов характер зависимости практически линейный.

При сравнительно высоких концентрациях величина удельной адсорбции стремится к некоторому постоянному предельному значению Г_∞, которое соответствует образованию на поверхности насыщенного мономолекулярного слоя сорбированных молекул. По величине предельной адсорбции можно дать количественную оценку удельной поверхности сорбента:

,

где N_A – число Авогадро; S_M – площадь поперечного сечения молекулы адсорбата (для карбоновых кислот она примерно составляет 20,5·10⁻²⁰, для спиртов – 21,6·10²⁰ м²).

На среднем участке процесс адсорбции описывают либо при помощи уравнения Ленгмюра, либо эмпирическим уравнением Фрейндлиха

.

Уравнение Фрейндлиха имеет концентрационное ограничение применимости и используется для приблизительных расчетов удельной адсорбции на твердых сорбентах с неоднородной пористой поверхностью.

Уравнение изотермы адсорбции Ленгмюра, выведенное на основании термодинамических и кинетических характеристик адсорбции хорошо согласуется с экспериментальными данными в области как низких, так и высоких концентраций раствора. При низкой концентрации (произведение KC << 1, соответственно 1 + KC ≈ 1) Г = Г_∞KC, получается линейная зависимость адсорбции от концентрации раствора как в области Генри. При высокой концентрации раствора KC + 1 ≈ KC значение адсорбции стремится к своему предельному значению. Однако и уравнение Фрейндлиха и Ленгмюра применимы только в случае образования мономолекулярного слоя адсорбтива.

В случае полимолекулярной адсорбции изотерма адсорбции имеет более сложный характер. Для описания процесса применяют другие теории, например, БЭТ (Бруннауэра, Эммета и Тейлора), которую широко применяют при измерении удельной поверхности порошков и пористых материалов.

Для проверки применимости того или иного уравнения изотермы адсорбции используют линейную форму уравнения. Если экспериментально полученные данные располагаются на этой прямой, то уравнение применимо. В этом случае возможно определить входящие в уравнение изотермы постоянные.

Линейная форма уравнения Фрейндлиха определяется в логарифмических координатах lgГ = f(lgC):

.

Если при этом экспериментальные точки укладываются на прямую, то результаты опытов согласуются с уравнением Фрейндлиха. Отрезок ординаты, отсекаемый прямой равен lga, а тангенс угла наклона – 1/n.

Приведение уравнения Ленгмюра к линейному виду возможно двумя способами:

1) .

При такой записи уравнения Ленгмюра график зависимости строят в координатах 1/Г – 1/С. Свободный член полученного уравнения прямой равен 1/Г_∞, а угловой коэффициент – .

2) .

В этом случае график зависимости строят в координатах С/Г – С. Свободный член полученного уравнения прямой равен , а угловой коэффициент – 1/Г_∞.