логика билеты. Формы мышления Объектом логического исследования являются "формы" мышления понятие, суждение, умозаключение. Логику интересует правильное, истинное мышление. Понятие форма мышления
 Скачать 280.66 Kb. Скачать 280.66 Kb.
|
|
10. Простые суждения. Суждение — форма мышления, в которой что-либо утверждается или отрицается о предмете, его свойствах или отношениях между предметами. Виды суждений и отношения между ними изучаются в философской логике. Простые суждения — суждения, составными частями которых являются понятия. Простое суждение можно разложить только на понятия. Состав простого суждения Простое (атрибутивное) суждение — это суждение о принадлежности предметам свойств (атрибутов), а также суждения об отсутствии у предметов каких-либо свойств. В атрибутивном суждении могут быть выделены термины суждения — субъект, предикат, связка, квантор. Субъект суждения — это мысль о каком-то предмете, понятие о предмете суждения (логическое подлежащее). Предикат суждения — мысль об известной части содержания предмета, которое рассматривается в суждении (логическое сказуемое). Логическая связка — мысль об отношении между предметом и выделенной частью его содержания (иногда только подразумевается). Квантор — указывает, относится ли суждение ко всему объёму понятия, выражающего субъект, или только к его части: «некоторые», «все» и т. п. Классификация простых суждений По качеству Утвердительные — S есть P. Пример: «Люди пристрастны к самим себе». Отрицательные — S не есть P. Пример: «Люди не поддаются лести». По объёму Общие — суждения, которые справедливы относительно всего объёма понятия (Все S суть P). Пример: «Все растения живут». Частные — суждения, которые справедливы относительно части объема понятия (Некоторые S суть P). Пример: «Некоторые растения суть хвойные». По отношению Категорические — суждения, в которых сказуемое утверждается относительно субъекта без ограничений во времени, в пространстве или обстоятельствах; безусловное суждение (S есть P). Пример: «Все люди смертны». Условные — суждения, в которых сказуемое ограничивает отношение каким-либо условием (Если А есть В, то С есть D). Пример: «Если дождь пойдет, то почва будет мокрая». Для условных суждений Основание — это (предыдущее) суждение, которое содержит условие. Следствие — это (последующее) суждение, которое содержит следствие. 11. Аналогия Аналогия Умозаключение по аналогам, или аналогия, представляет собой один из видов рассуждений индуктивного типа. Аналогия — это сходство между предметами, явлениями и т.д. Умозаключение по аналогии (или просто аналогия) — это индуктивное умозаключение, при котором на основе сходства двух объектов по некоторым параметрам совершается заключение об их сходстве, а также и по другим параметрам. Например, планеты Марс и Земля сходны по следующим параметрам: они расположены в Солнечной системе, на обеих планетах есть вода, атмосфера и т.д. На Земле есть жизнь, и поскольку Марс похож на Землю с точки зрения условий, являющихся необходимыми для существования живого, то можно заключить, что на Марсе также есть жизнь. Это заключение правдоподобно. Общая схема умозаключения по аналогии: объект А имеет признаки а, b, с. Объект В сходен с A в том,что имеет признаки а и b. Значит, объект В имеет, вероятно и признак с. Сопоставление двух объектов может дать предположительное знание, гипотезу, нуждающуюся в дальнейшей проверке. Иногда аналогия проявляется в форме, напоминающей популярную индукцию. Например, ученик прочел «Евгения Онегина» А.С, Пушкина — понравилось, прочел «Пиковую даму»— тоже понравилось. На этом основании он заключает, что и «Капитанская дочка» ему тоже будет интересна. Здесь от знания об отдельных объектах совершается переход к знанию еще об одном индивидуальном объекте. Таким образом, умозаключение по аналогии весьма редко присутствует в ясной, не требующей дополнительного размышления и реконструкции форме. Зачастую аналогия является свернутой, когда ее некоторые части опускаются. Рассуждения, которые заведомо не являются умозаключениями по аналогии, также могут называться аналогией. Помимо аналогии свойств существует аналогия отношений, поскольку уподобляться друг другу и быть сходными могут не только предметы, но и отношения между ними. При аналогии отношений уподобляются лишь отношения, а предметы, между которыми эти отношения имеют место, могут быть абсолютно разными. Аналогия означает некоторое подобие и сходство вещей, свойств, отношений. Но не всякое сходство есть аналогия. Например, два близнеца похожи друг на друга, но нельзя сказать, что они —«аналоги» друг друга. Аналогия — частный случай сходства, которое сопряжено с различием и без него не существует. По этой причине аналогия представляет собой попытку продолжить сходство несходного. Умозаключение по аналогии не дает достоверного знания. Посылки умозаключения по аналогии могут быть истинными, но это не означает, что его заключение также получится истинным. Например, квадрат и прямоугольник — плоские геометрические фигуры, их противоположные стороны равны и параллельны. У прямоугольника все углы прямые. По аналогии заключаем, что у квадрата все углы также прямые. Этот вывод истинный. Продолжим рассуждения из сходства квадрата и прямоугольника, и того, что у квадрата все стороны равны, по аналогии получаем вывод, что и у прямоугольника все стороны тоже равны. Этот вывод не является истинным. Вероятность истинности вывода, получаемого по аналогии, может быть различной. Та аналогия, которая дает истинное знание с большой вероятностью, называется строгой, или точной. Строгими аналогиями являются аналогии научные, в отличие от встречающихся в повседневной жизни, как правило поверхностных и не строгих. Чтобы аналогия была строгой, важен характер связи сходных признаков предметов с переносимым признаком: информация о сходстве должна иметь тот же тип, что и переносимая на другой предмет. Если исходное знание внутренне связано с переносимым признаком, то вероятность вывода существенно повышается.
законы логики – это такие сложные суждения, которые являются истинными в силу своей логической формы, т.е. только на основании связи составляющих их суждений. Закон исключенного третьего Аристотель формулировал следующим образом: «Если мы имеем два противоречащих высказывания, т.е. таких, в одном из которых (А) что-либо утверждается, а в другом то же самое отрицается (не-А), то, по крайней мере, одно из них истинно». Иначе говоря, противоречащие высказывания не могут быть оба ложными. Другой, также аристотелевский закон – закон противоречия – может быть выражен так: из двух противоречащих высказываний А и не-А, по крайней мере, одно является ложным, или, иными словами, противоречащие друг другу высказывания не могут быть вместе истинными. закона тождества: каждая объективно истинная и логически правильная мысль или понятие о предмете должны быть определенными и сохранять свою однозначность на протяжении всего рассуждения и вывода. Закон тождества ориентирует нас на то, чтобы в процессе рассуждения любая мысль оставалась тождественной самой себе. Хотя в реальном мире абсолютного тождества не существует. Тем не менее между вещами и явлениями всегда возможно частичное тождество. Мышление выделяет именно эту сторону действительности, обеспечивая тем самым определенность и устойчивость содержания мысли. Ошибки, связанные с нарушением требований этого закона, можно разделить на три вида: эквивокация, логомахия, амфиболия. Содержание эквивокации состоит в том, что рассуждающий несколько раз использует многозначное слово то в одном, то в другом значении, считая, что использует слово однозначно. То, что называют законом достаточного основания, есть также определенное требование, необходимое условие правильности нашего мышления. Оно состоит в том, что в процессе познания можно принимать то или иное суждение, высказывание за истину лишь на достаточном основании. Основания истинности (ложности) некоторого утверждения являются объективно достаточными, если предъявление этих оснований разумному субъекту убеждает его в истинности (ложности) этого утверждения. Четыре основных формально-логических закона отражают важные свойства правильного мышления – определенность, непротиворечивость, последовательность, обоснованность, четкость. 13.Виды суждений. Объединенная классификация. При анализе простых категорических суждений в них необходимо различать как качественную, так и количественную стороны. С точки зрения качества связки суждения делятся на две группы: утвердительные и отрицательные. В утвердительных суждениях логическая связка приписывает предикат суждения субъекту. Например, в суждении «Высокая степень квалификации специалиста требует его основательной предварительной подготовки» к субъекту суждения (S) «высокая степень квалификации специалиста» с помощью утвердительной связки (не высказанной в языке) приписывают предикат суждения, (Р) – «требует его основательной предварительной подготовки». В отрицательных суждения логическая связка отделяет предикат от субъекта суждения. Например: «Рыбы не являются млекопитающими». В этом суждении связка отрицательная, так как признак «млекопитающие», составляющий предикат суждения (Р), несовместим с понятием «рыбы» (S). Логическая связка суждения считается отрицательной только в тех случаях, когда отрицательная частица «не» стоит перед связкой. Если же эта частица стоит после связки, то она входит в состав предиката, а суждение относится к разряду утвердительных. Оба вида суждения не должны метафизически противопоставляться: с логической точки зрения любое из них может быть преобразовано в свою противоположность. Те частные суждения, где количественная сторона известна лишь частично (по крайней мере, некоторые), называются неопределёнными частными суждениями. Более важной для познания формой суждения является общее суждение, где объём субъекта относится ко всем предметам данного класса. 2 Объединённая классификация суждений по качеству и количеству. В логике принято классифицировать категорические суждения по их объединённому признаку, учитывающему взаимосвязь как качественной, так и количественной стороны суждения. В объединённой классификации суждения делятся на четыре вида. Общеутвердительные суждения. Это суждение является общим по количеству и утвердительным по качеству. Символически эти суждения записываются следующим образом: «Все S есть P», где количественная («все») и качественная («есть») стороны суждения явно выражены в языке. Например: «Все звёзды светятся собственным светом», «Все птицы имеют крылья», «Все студенты сдают экзамены», и т. п.. Сокращённо общеутвердительные суждения обозначаются буквой А (первой буквой от латинского слова affirto, что в переводе означает утверждаю). Общеотрицательные суждения. Это суждение является общим по количеству и отрицательным по качеству. Обобщённая формула этого суждения такова: «Ни одно S не естьP», где количественная («ни одно») и качественная («не есть») стороны суждения явно выражены в языке. Например: «Ни одна нация не может существовать без общего языка», или «ни один организм не может жить без пищи» и так далее.. Общеотрицательные суждения символически обозначается буквой Е (взята первая гласная буква от латинского слова nego, что в переводе означает отрицаю). Частноутвердительное суждение. Это суждение является частным по количеству и утвердительным по качеству. Его обобщённая формула выглядит так: « Некоторое S есть P», где количественная («некоторые») и качественная («есть») стороны суждения явно выражены в языке. Например: «Некоторые студенты являются отличниками», или «Некоторые рыбы летают» и так далее.. Сокращённо частноутвердительные суждения обозначаются I (вторая гласная буква от латинского слова affirto). Частноотрицательные суждения. Это суждения является частным по количеству и отрицательным по качеству. Его символическая формула такова: «Некоторые S не есть P», где количественная («некоторые») и качественная («не есть») стороны суждения явно выражены в языке. Например: «Некоторые страны Африки не являются мусульманскими», или «Некоторые студенты не посещают задания занятия в спортивных секциях» и т. п.. Эти суждения обозначаются буквой O (второй гласной буквы от латинского слова nego). Единичные суждения из объединённой классификации категорических суждений в самостоятельную группу не выделяются. По своей логической характеристике с точки зрения количества все единичные суждения относятся к общим суждениям: либо к общеотрицательным.
Логическое деление понятий предполагает соблюдение ряда необходимых правил. 1. Деление должно быть соразмерным, т.е. общий объем членов деления должен равняться объему делимого родового понятия. Это правило гарантирует от двух возможных ошибок: неполного (с остатком) или обширного (с избытком) деления. Например, деление понятия «право» на государственное, гражданское, административное, уголовное будет неполным (ибо есть еще семейное, сельскохозяйственное и пр. виды), т.е. с остатком; деление же понятия «дерево» на лиственное, хвойное, высокое, низкое, зеленое и т.д. будет широким, с избытком (указанные видовые признаки взяты по разным основаниям, отсюда и избыток членов деления). 2. В каждом акте деления необходимо применять только одно основание, т.е. производить деление родового понятия по видоизменению одного и того же существенного признака. Только переходя к следующей ступени деления на подвиды, следует менять основание деления, пока не будут выявлены самые низшие классы предметов. При нарушении этого правила теряется стройность деления, возникает путаница, как в случае с предыдущим примером с «деревом». 3. Члены деления должны взаимно исключать друг друга. Согласно этому правилу члены деления должны быть соподчиненными понятиями, их объемы не должны перекрещиваться. Например, понятие «литература» может быть разделено на понятия «художественная», «научная», «техническая», «учебная», но если в этот перечень будут включены такие понятия, как «переводная», «новая» («старая»), «дорогая» и т.п., то это будет ошибкой, т.к. указанные объемы будут перекрещиваться (художественная литература может быть переводная, а может быть оригинальная, например, и т.д.). Деление должно быть последовательным, т.е. делимое понятие должно представлять ближайший род для членов деления, а члены деления должны быть непосредственными видами делимого понятия. Нельзя переходить к подвидам, минуя непосредственные видовые понятия. Примером нарушения такого правила будет деление понятия «дома» на кирпичные, панельные, деревянные, многоэтажные, старые, обычные, элитные и т.д. Видовые понятия «кирпичные», «панельные», «деревянные» будут конкретизированы подвидами «многоэтажные», «одноэтажные»; те же, в свою очередь, будут делиться на «старые» или «новые» и т.д.
Каждая наука, в том числе логика, строит свой язык на базе естественного языка, а именно формируя специальные слова, термины, особые знаки (символы). Одно и то же слово естественного языка в разных науках имеет разное значение. Например, значение слова «термин» в логике используется для обозначения элементов суждения и умозаключения и выступает как синоним слова «понятие». В данном пособии уже использованы некоторые специальные слова «языка» логики, такие как субъект, предикат, связка, термин и пр. Необходимо, чтобы основополагающие понятия определялись строго, а их значения оставались одинаковыми в рамках одного учения, теории. Поскольку некоторые основополагающие понятия (категории) логика заимствует из философии, то сама логика их определять не может, например: «противоречие», «тождество», «различие» и пр. Однако остальные слова «языка» логики должны своевременно определяться. Обычно знакомство с «языком» логики происходит по мере ее познания. В действительности, символика традиционной формальной логики немногочисленна, и эту символику необходимо знать и уметь ею пользоваться, переводить ее на естественный язык и наоборот. Основные символы, заменяющие главные понятия логики, S и P используются для обозначения понятий субъекта, или предмета мысли, и предиката, признака предмета мысли соответственно. Понятия «субъект» и «предикат» также используются и в философии, но имеются различия между их философским и логическим значениями. Именно в философии «субъект» — это то, что противостоит «объекту» — природе, миру в целом. По этой причине субъектом в данном смысле становится и один человек, и все человечество, т.е. общество. В логике же «субъект» — предмет мысли, о чем ведется рассуждение, это логическое подлежащее суждения. С точки зрения логики субъектом может выступать любое понятие, отражающее любой реальный или мнимый, материальный или идеальный «предмет», поскольку предметом мысли может быть все, что угодно.
Объективные отношения между самими предметами находят свое отражение в отношениях между понятиями. Все многообразие этих отношений также можно классифицировать на основе содержания и объема понятий. Сравнимые и несравнимые понятия. Сравнимыми называют понятия, в содержании которых имеется хотя бы один общий признак. Почти все понятия являются сравнимыми. В данном случае опровергается известная пословица «Нельзя сравнивать Божий дар с яичницей». С точки зрения логики, это также сравнимые понятия, так как о них, по крайней мере, можно сказать, что и то, и другое – предмет. Это и будет их общий признак. Несравнимыми называют понятия, в содержании которых нет ни одного общего признака. Некоторые авторы в качестве примера несравнимых понятий приводят понятия «предмет» и «свойство». Сравнимые понятия могут быть совместимыми или несовместимыми. Совместимые и несовместимые понятия. Понятия называются совместимыми, если их объемы имеют хотя бы один общий элемент. Несовместимые – это понятия, в объемах которых нет ни одного общего элемента. Обычно отношения между понятиями изображают с помощью так называемых кругов Эйлера (рис. 2, 3). Виды совместимых понятий. Совместимые понятия могут быть равнозначными (тождественными), перекрещивающимися, а также подчиненным и подчиняющим. Равнозначные (тождественные) - это понятия, объемы которых полностью совпадают (рис. 2, а). Пример. А – понятие «автор романа «Анна Каренина»»; В – понятие «автор романа «Война и мир»». Перекрещивающиеся - это понятия, объемы которых частично совпадают 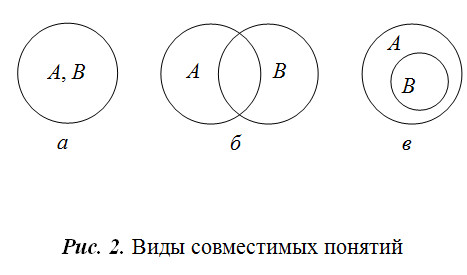 Перекрещивающиеся - это понятия, объемы которых частично совпадают (рис. 2, б). Пример. А – понятие «студент»; В – понятие «спортсмен». Подчиняющее и подчиненное понятия. Объем подчиненного понятия полностью входит в объем подчиняющего, не исчерпывая его (рис. 2, в). Пример. А – понятие «деревья»; В – понятие «береза». Виды несовместимых понятий. Несовместимые понятия бывают соподчиненными, противоположными (контрарными) и противоречащими (контрадикторными). Соподчиненные – это понятия, объемы которых различны и входят в объем общего для них понятия, не исчерпывая его (рис. 3, а). Пример. А – понятие «фиалка»; В – понятие «роза»; С – понятие «цветы». 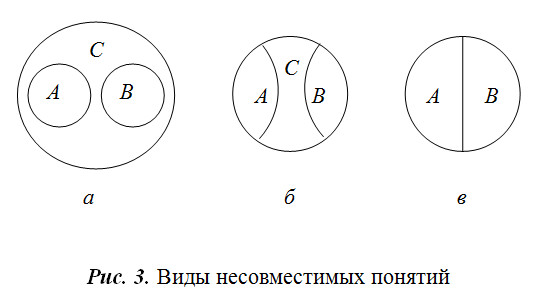 Противоположными (контрарными) понятиями являются такие, которые соподчинены третьему понятию и представляют собой крайние степени выраженности некоторого качества. Можно сказать, что их объемы занимают полярные места в объеме общего для них понятия (рис. 3, б). Пример. А – «черный»; В – «белый»; С – «цвет». Противоречивые (контрадикторные) понятия подчиняются общему для них понятию, и при этом в общем понятии не существует такого элемента, который не был бы элементом одного из этих понятий. Их объемы делят объем общего для них понятия на две части (рис. 3, в). Пример. А – «монархия»; В – «республика». Общим для этих понятий является понятие «форма правления». Причем «монархия» и «республика» – несовместимые формы правления, и в то же время других форм правления не существует. С помощью кругов Эйлера можно получать достаточно сложные схемы. Например, можно изобразить отношение между понятиями А – «студент», В – «спортсмен», С – «мастер спорта», D – «кандидат в мастера спорта» (рис. 4). 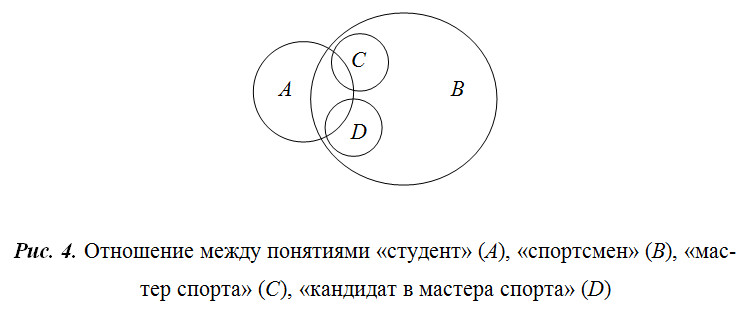 Изучение отношений между понятиями имеет огромное значение для правильного употребления понятий в устной и письменной речи. И наоборот, незнание этих отношений способно повлечь за собой искаженное отражение действительности – отношений между самими вещами. |
