логика билеты. Формы мышления Объектом логического исследования являются "формы" мышления понятие, суждение, умозаключение. Логику интересует правильное, истинное мышление. Понятие форма мышления
 Скачать 280.66 Kb. Скачать 280.66 Kb.
|
30.Операции с классами.А, т. е. А или не А, третьего не дано (tertium поп datur).32. Доказательство. Виды доказательства. Спор. По способу доказывания доказательства бывают прямыми и косвенными. Прямое доказательство — это обоснование тезиса аргументами без помощи каких-либо дополнительных построений. Рассуждение в этом случае начинается с аргументов и с логической необходимостью приводит к обоснованию истинности тезиса. Доказательство в таком случае осуществляется в форме дедуктивного умозаключения. истинность тезиса обосновывается посредством опровержения истинности противоречащего положения, иначе говоря, путем доказательства ложности антитезиса. К косвенному доказательству прибегают тогда, когда выдвинутый тезис нельзя доказать прямо, когда не располагают аргументами, обосновывающими тезис непосредственно. Косвенное доказательство имеет два вида: апагогическое и разделительное.Апагогическое косвенное доказательство (от греч. apagoge — вывод и apagogos — уводящий, отводящий) — непрямое, или как бы в сторону направленное, доказательство. Здесь к истинности тезиса приходят путем доказательства ложности антитезиса. Например, требуется доказать тезис А. Аргументов, прямо обосновывающих этот тезис, нет. Тогда высказываем суждение, противоречащее тезису, т. е. выдвигаем антитезис не А и допускаем, что он истинный (говорят: допустим, истинным является не А). Допустив , что антитезис не А является истинным, мысленно выводим из него следствия и проверяем их. Если будет установлено, что выведенные из антитезиса следствия в действительности не существуют, и их существование вообще немыслимо (абсурдно) либо они противоречат ранее доказанным положениям, то тем самым будет доказана ложность антитезиса не А. Вывод о ложности антитезиса делается на основании такого правила условно-категорического силлогизма: из ложности следствия с необходимостью вытекает ложность основания. Доказав ложность антитезиса не А, затем в соответствии с требованием закона исключенного третьего переходят к истинности тезиса А.Апагогическое косвенное доказательство называют еще сведением к абсурду (reductio ad absurdum). В математических и некоторых других науках оно получило название доказательства от противного. Апагогическое косвенное доказательство довольно часто используют в судебном доказывании. В разделительном косвенном доказательстве тезис обосновывается путем исключения всех членов разделительного суждения (всех предикатов), кроме одного, являющегося доказываемым тезисом. Строится разделительное косвенное доказательство так. Допустим, требуется доказать тезис: "S есть Р". Если известно, что 5 может быть не только Р,, но и Р2 и /*3, и затем установлено, что S не является ни Р2, ни Р3, то тем самым будет доказано положение о том, что "51 есть Р". Такого рода косвенные доказательства также довольно часто используются в судебном доказывании.Прямые и косвенные доказательства в логике нельзя путать с таковыми в уголовном процессе. В логике под доказательством понимают мыслительный процесс обоснования истины, в уголовном же процессе доказательство — это доказательственный факт, факт действительности Доказательство тесно связано с опровержением. Опровержение может быть направлено против тезиса, против аргументов либо против способа доказательства. В соответствии с этим различают такие способы опровержения: опровержение тезиса; опровержение аргументов; опровержение связи тезиса с аргументами.Знания правил и схем логических умозаключений, умения приводить убедительные доводы в защиту своей точки зрения, делать обобщения из имеющихся фактов и свидетельств — иными словами, логической культуры, явно недостаточно для целенаправленной полемики или дискуссии. Ведь нас убеждают не только логические аргументы и доводы оратора, но и его эмоциональные и нравственные качества, не говоря уже о красоте и изяществе самой речи. Не случайно Платон и Аристотель, закладывая основы риторики, обращали внимание на формирование этих качеств.Ознакомление с психическими процессами, связанными с убеждением и мотивацией действий человека, важно с двух точек зрения. Во-первых, оно дает возможность оратору дополнить логические доводы психологическими и тем самым усилить убедительность своей аргументации. Одновременное воздействие на ум и душу всегда убеждает человека сильнее и глубже, чем при обособленном подходе, а тем более когда один подход противопоставляется другому. Во-вторых, зная особенности протекания психических процессов, можно избежать психологических уловок, которые часто используются оппонентом в ходе полемики. Такие уловки многочисленны и рассчитаны главным образом на то, чтобы вывести противника из душевного равновесия, заставить его делать промахи, потерять нить аргументации, — в результате победа в споре обеспечена.
Логический квадрат придумали в средние века. Выглядит он вот так 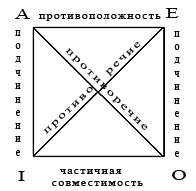 Логический квадрат показывает отношения между суждениями с одинаковыми субъектами и предикатами, но разными связками и кванторами. С его помощью можно делать выводы относительно истинности и ложности таких суждений. Однако выводы еще проще делать с помощью предложенного стульчика. Инструкция прилагается: 1. У нас 3 «дороги»: AE (EA ), AO (OA) и EI (IE). 2. Отношения противоречия - AO (OA) и EI (IE) устроены одинаково Если суждение с одной стороны истинно, то с другой – ложно и наоборот. (Это так называемый закон исключенного третьего - истинно или само высказывание, или его отрицание, а третьего не дано). 3. Отношения противоположности - AE (EA ). Если с одной стороны суждение истинно, то с другой – ложно. Но если с одной стороны суждение ложно, то другое может быть как ложным, так и истинным – однозначный вывод мы сделать не можем. Например: Если ложно, что все бананы являются спелыми, то ложным может быть и утверждение, что все бананы не являются спелыми. Истинным может быть – некоторые бананы являются спелыми. Как делать выводы. Парочка примеров с подробным описанием. Исходное суждение: Ни одна мышь не является подмышкой 1. Если не указано, что это суждение ложно (не верно), то оно истинно. Данное суждение – общеотрицательное. Обозначается буквой E. 2. Смотрим на стульчик. Начинаем движение с E. Мы можем пойти по EI и по EA 3. Пойдем по EI. Если E – истинно, то I будет ложно. Обозначается Ī . Читается: Неверно, что I. В нашем случае: неверно, что некоторые мыши являются подмышками. 4. Теперь пойдем по EA. Если E – истинно, то A будет ложно. Ā: Неверно, что все мыши являются подмышками. 5. Мы определили, что A ложно, значит, по AO O будет истинным. O: Некоторые мыши не являются подмышками. Как это должно выглядеть письменно: Ни одна мышь не является подмышкой (E) Ī : Неверно, что некоторые мыши являются подмышками. Ā: Неверно, что все мыши являются подмышками. O: Некоторые мыши не являются подмышками. Теперь давайте рассмотрим пример с ложным общеотрицательным. Исходное суждение: Неверно, что все розетки не являются работающими 1. Данное общеотрицательное суждение – ложно. Обозначается Ē. 2. Смотрим на стульчик. Начинаем движение с E (в нашем случае Ē). У нас опять 2 пути - EI и EA. 3. Пойдем по EI. Если E – ложно, то I будет истинно. I: Некоторые розетки являются работающими. 4. Теперь пойдем по прямой EA. Если E – ложно, то мы не можем сделать однозначный вывод относительно истинности A. Не зная истинно A или ложно, нам не определить истинность O по диагонали. Получается только один достоверный вывод – I. Письменно: Неверно, что все розетки не являются работающими (Ē) I: Некоторые розетки являются работающими.
Фигуры и модусы категорического силлогизма В посылках простого категорического силлогизма средний термин может занимать место субъекта или предиката. В зависимости от этого различают четыре разновидности силлогизма, которые называют фигурами. В первой фигуре средний термин занимает место субъекта в большей и место предиката в меньшей посылках. Во второй фигуре – место предиката в обеих посылках. В третьей фигуре – место субъекта в обеих посылках. В четвертой фигуре – место предиката в большей и место субъекта в меньшей посылке. Данные фигуры исчерпывают все возможные комбинации терминов. Фигуры силлогизма – это его разновидности, различающиеся положением среднего термина в посылках. Посылками силлогизма могут быть суждения, различные по качеству и количеству: общеутвердительные (А), общеотрицательные (Е), частноутвердительные (I) и частноотрицательные (О). Разновидности силлогизма, различающиеся количественными и качественными характеристиками посылок, называются модусами простого категорического силлогизма. Каждая фигура имеет свои особые правила, которые выводятся из общих. Правила 1–й фигуры: – большая посылка – общее суждение; – меньшая посылка – утвердительное суждение. 1–я фигура – наиболее типичная форма дедуктивного умозаключения. Из общего положения, выражающего нередко закон науки, правовую норму делается вывод об отдельном факте, единичном случае, конкретном лице. Широко применяется данная фигура в судебной практике. Юридическая оценка (квалификация) правовых явлений, применение нормы права к отдельному случаю, назначение наказания за преступление, совершенное конкретным лицом, и другие судебные решения принимают логическую форму 1–ой фигуры силлогизма. Правила 2–й фигуры: – большая посылка – общее суждение; – одна из посылок – отрицательное суждение. Данная фигура применяется, когда необходимо показать, что отдельный случай (конкретное лицо, факт, явление) не может быть подведен под общее положение. Этот случай исключается из числа предметов, о которых сказано в большей посылке. В судебной практике 2–я фигура используется для заключений об отсутствии состава преступления в данном конкретном случае, для опровержения положений, противоречащих тому, о чем говорится в посылке, выражающей общее положение. Правила третьей фигуры: – меньшая посылка – утвердительное суждение; – заключение – частное суждение Давая только частные суждения, 3–я фигура применяется чаще всего для установления частичной совместимости признаков, относящихся к одному предмету. Например: Осмотр места происшествия (М) имеет одной из своих задач обнаружение следов преступления (Р) Осмотр места происшествия (М) – следственное действие (S) Некоторые следственные действия (S) имеют одной из своих задач обнаружение следов преступления (Р) В практике рассуждения 3–я фигура применяется сравнительно редко. 4–я фигура силлогизма также имеет свои правила и модусы. Однако выведение заключения из посылок по данной фигуре не характерно для естественного процесса рассуждения.
Сопоставление самых различных по содержанию суждений позволяет нам увидеть свойственную им общую структуру, то есть одинаковое формальное построение. Например, возьмём три суждения: «Все люди обладают сознанием» «Собаки – теплокровные животные». «Все государства имеют конституцию». се три предположения по форме являются суждениями и отражают самые разные стороны реальной жизни. Но при этом мы замечаем, что по своей структуре они идентичны, ибо все они содержат три части, или три элемента. Первый элемент называется субъектом суждения. Субъект суждения выражает знание о предмете суждения, то есть то, о чём говорится в данном суждении. Сокращённо субъект суждения обозначается буквой S (от латинского слова Subjektum). В приведённых примерах субъектом суждения являются: «все люди», «собаки», «все государства». При этом не следует отождествлять субъект суждения от предмера (объекта) суждения, то есть от того, что в реальной деятельности познаётся с помощью суждения. Действительно предмет всегда богаче, чем какое-либо значение о нём, выраженные субъектом суждения. Предмет суждения отличается от субъекта суждения так же, как мысль о предмете от самого предмета. Вторым логическим элементом суждения является предикат суждения. Он выражает знание о признаке предмета суждения, то есть то, что говорится о субъекте суждения. Сокращённо предикат обозначается буквой P (от латинского слова predikatum). Предикат суждения является вторым необходимым элементом суждения. элементом суждения является связка. Она выражает отношение, которое устанавливается в суждении между субъектом и предикатом. Связка придаёт ограниченное единство и законченность всей форме суждения. Логическая связка между субъектом и предикатом имеет две формы. Она может быть либо утвердительной, либо отрицательной – в зависимости от того, приписывается предикат субъекту или нет. В русском языке связка как правило не высказывается, а подразумевается. Если мы говорим «Все люди – разумные существа», то S(все люди) и P(разумные существа) связываются с помощью тире; но в других случаях вместо слова «есть» могут использоваться «суть», «имеется» и топу подобное (имеется в виду утвердительная форма. Отрицательная форма выражается связкой «не есть», «не суть», «не имеется», «не является» и т.п.. Например, «Птицы не являются млекопитающими животными». Здесь опят мы видим все три элемента суждения.) У всех народов и во всех языках простейшая форма суждения сводится к трёхчленной схеме, поэтому, несмотря на различия языков, возможен перевод мысли с одного из них на другой. Таким образом, структура простого категорического суждения, которое всегда состоит из трёх элементов, может быть выражена в виде общей формулы: S – P, где тире обозначает связку; другие два элемента (S и P) несут смысловую нагрузку. В ложне они называются ещё переменными, так как могут выражать различное конкретное содержание. Связка же в простом категорическом суждении не является переменной частью суждения, она выражает только утвердительное или отрицательное отношение между S и P и может быть названа постоянным элементом суждения. Несколько своеобразно проявляется трёхчленная структура простых суждений в так называемых суждениях существования и в суждения отношений. Обычно суждениями существования называют такие, которые в своём конкретном содержании выражают сам факт существования или несуществования отражаемого в мысли предмета. Суждения существования по форме делятся на утвердительные и отрицательные. В утвердительных суждения устанавливается наличие предмета, его существования. Например, «Планеты существуют», «Существуют информационные технологии, позволяющие людям общаться независимо от их местонахождения» и т.д.. В отрицательных суждениях указывается на отсутствие предмета; «Нет птицы без перьев» и т.д. Специфической особенностью суждений отношений является то, что в их трёхчленной структуре роль предиката выполняет третье понятие, которое имеет также определённое смысловое значение, помимо основного предиката. Например, «Иван брат Петра», или «Кавказские горы выше Карпат», и т.д.. Структура таких суждений может быть выражена формулой «a R b», где a и b выражают понятия, а символ R обозначает определённое содержательное отношение между мыслимыми в суждении предметами мысли. Фактически в таких суждениях третий элемент (R) выполняет роль связки. |
