|
|
Лекции по физике 4 семестр. Фотон обладает массой m
Фотоэффект.
Фотон обладает массой mф=Ћω/c2 и импульсом p= mфc=Ћω/c=k·Ћ.
Квантование энергии означает, что излучение представляет собой поток фотонов, однако они не являются частицами, фотонов равна нулю. В отличии от классических частиц эти выражения связываются между собой корпускулярные характеристики с волновыми (частотой и длиной волны):
ε=Ћω=2πЋc/λ, так как ω=2πc/Tc=2πc/λ.
Свет распространяется и поглощается веществом отдельными порциями. Каждый квант поглощается одним электроном.
Явление фотоэффекта: кванты электромагнитного излучения воздействуют на электроны твёрдых и жидких тел.
С помощью потенциометра можно менять также и знаки полюсов катода и анода. Если кванты вырывают свободные электроны из катода, то имеет место внешний фотоэффект.
Ћω=A+T (T=mv2/2)
Фотоэффект может произойти, когда εк≤A.
Если освещать катод лучами с разными частотами, постоянно переходя от более длинных к более коротким волнам, то фотоэффект начнёт наблюдаться при. Она называется красной границей фотоэффекта. Энергия кванта в этом случае равна работе выхода.
Ћω==Ћωкр+Т
Ћ(ω-ωкр)=mv2/2
Ћ=mv2/2(ω-ωкр)=tgα
Скорость электрона зависит от частоты излучения, вызывающего фотоэффект, но не зависит от интенсивности.
Выход электрона из катода очень мал: 0,001 падающих квантов. Остальные поглощаются, не вырывая электронов.
Внутри баллона нет тока, потому что нет носителей, при облучении катода в цепи появляется ток и при увеличении U ток растёт, потому что всё большее число электронов достигает анода и, начиная с некоторого напряжения ток, не изменяется, потому что все электроны, вышедшие за единицу времени, достигают анода. При U=0 I<>0 и это объясняется тем, что электроны вылетают с некоторой скоростью. Чтобы убрать анодный ток, нужно приложить задерживающее напряжение.
При U=Uзад ни один из электронов, который обладает максимальной скоростью, не может преодолеть задерживающее напряжение:
mv2/2=eUзад,e<0, U<0.
Для того чтобы убрать ток- переполюсовка.
Некоторые сведения из специальной теории относительности Эйнштейна.
Фотоны распространяются со скоростью света.
Полная энергия частицы может быть представлена как:
E=m0c2/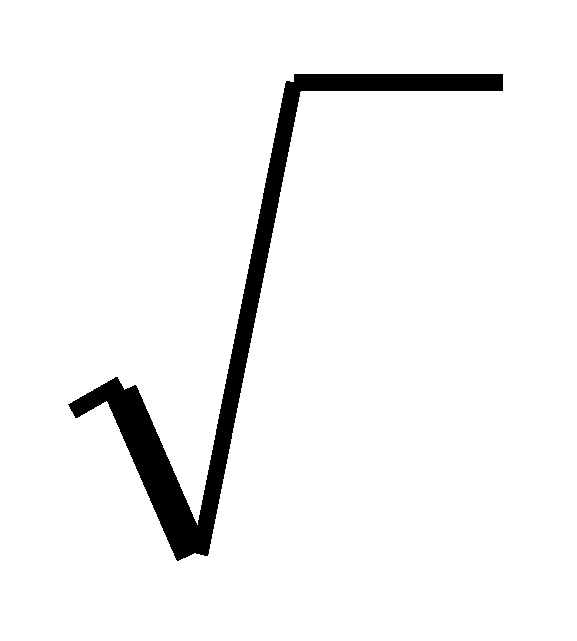 (1-v2/c2); m=m0/ (1-v2/c2); m=m0/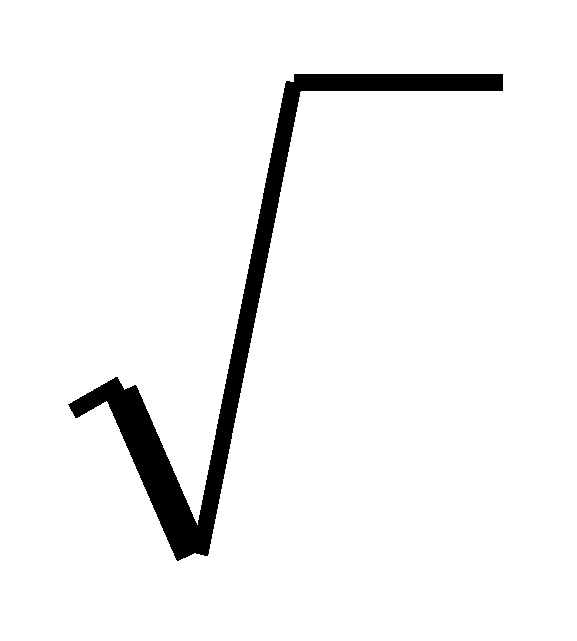 (1-v2/c2); (1-v2/c2);
m0-масса покоя в той системе, где частица покоится.
В полную энергию не входит потенциальная энергия частицы во внешнем силовом поле
E= m0c2+T
Для покоящихся тел
Найдём кинетическую энергию релятивисткой частицы, т. е. частицы, масса которой зависит от скорости.
приращение Т равно А:
dT=dA=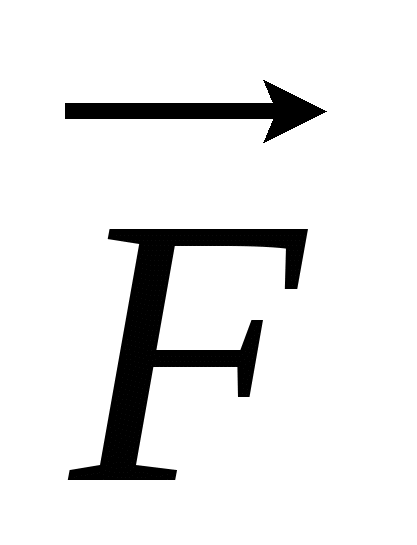 ·d ·d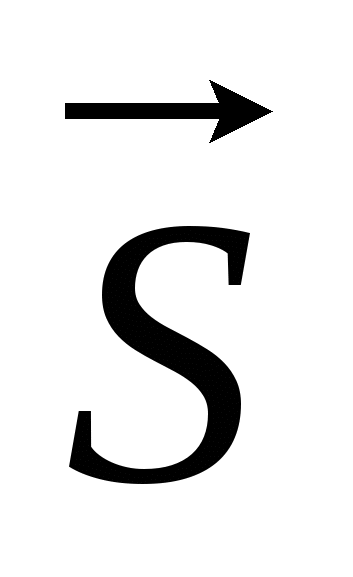 ; ; 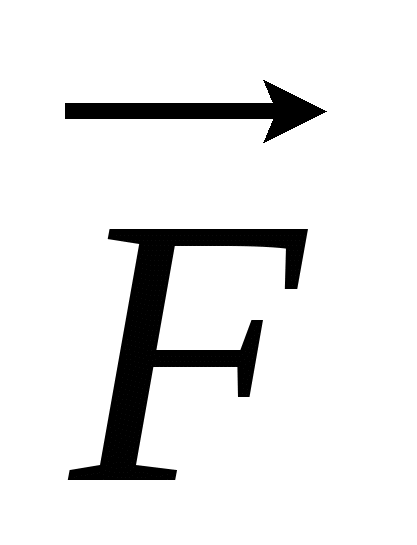 =d =d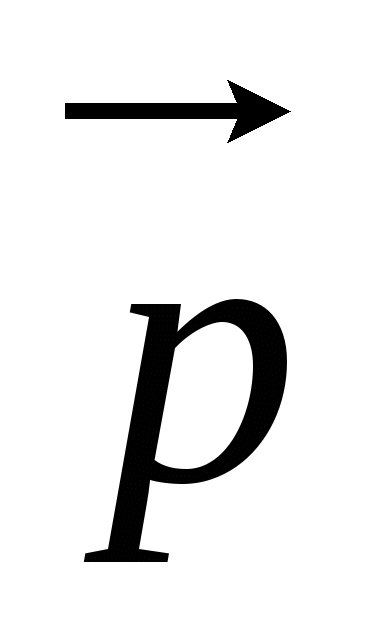 /d /d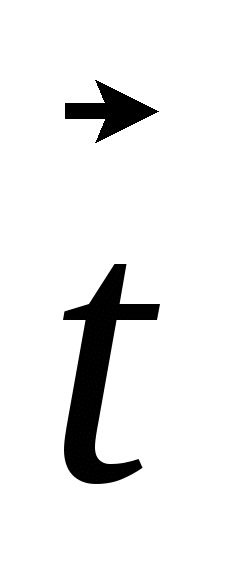 , d , d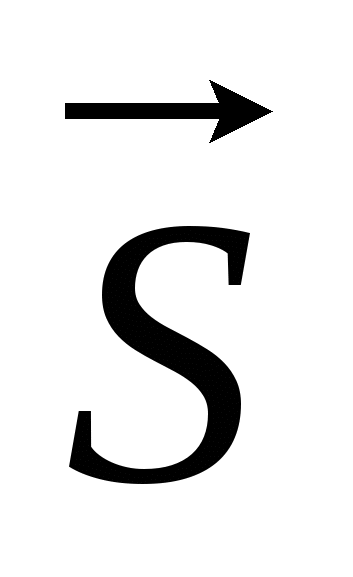 = =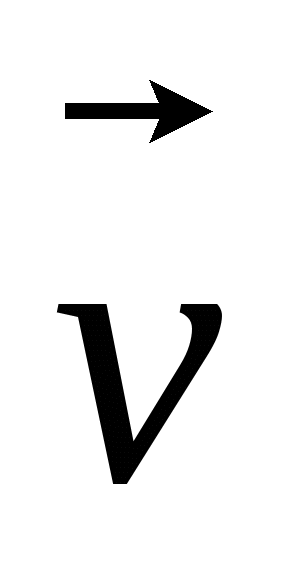 dt; dt;
dT= d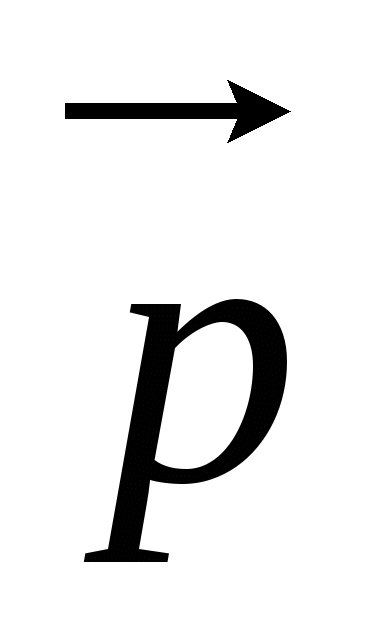 /d /d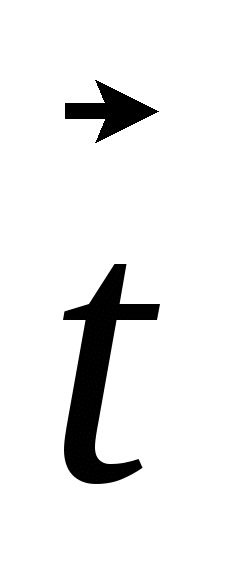 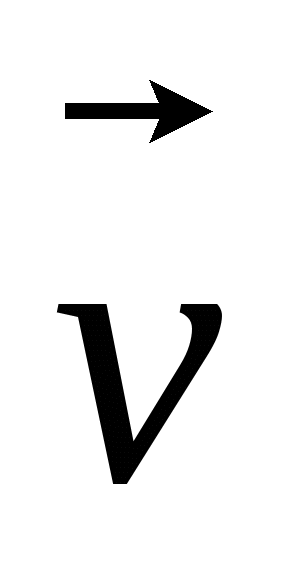 dt= d dt= d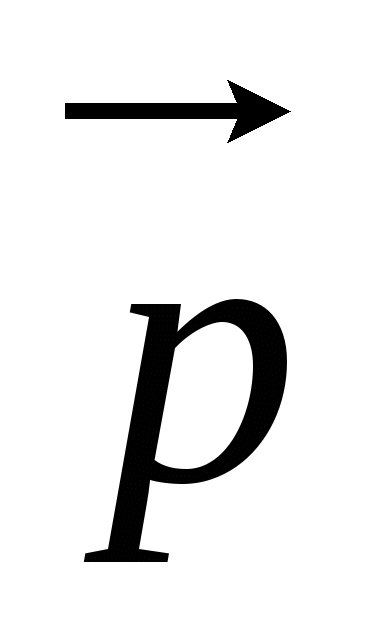 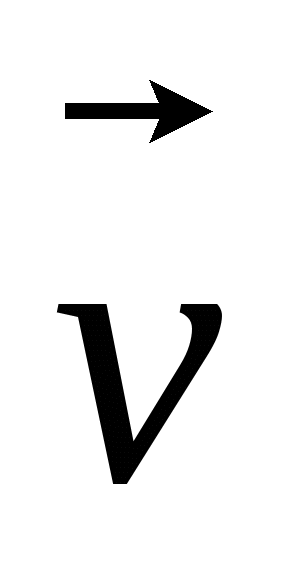
dT=d(m0v/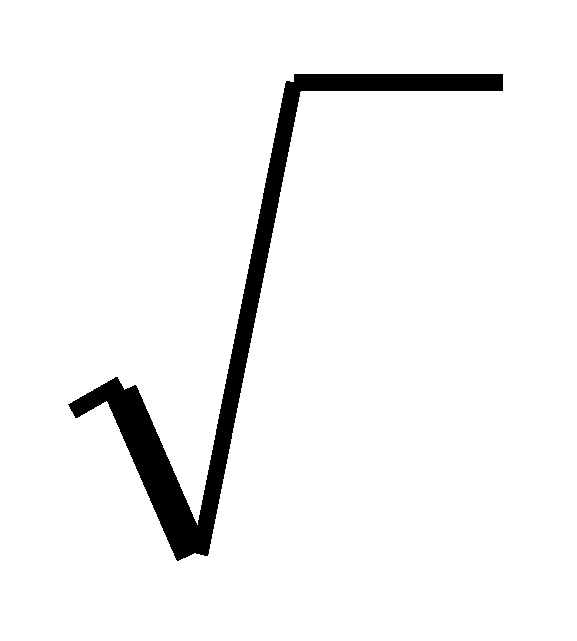 (1-v2/c2))/dt*( (1-v2/c2))/dt*(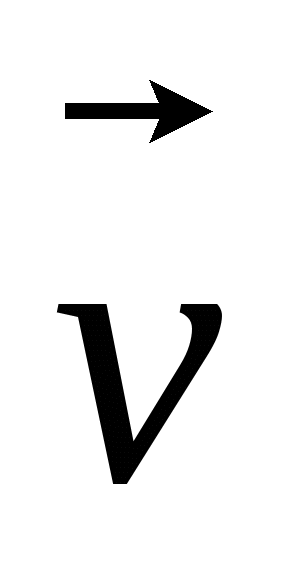 dt)= dt)= 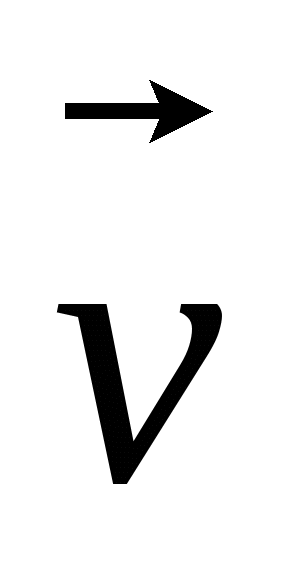 d(m0v/ d(m0v/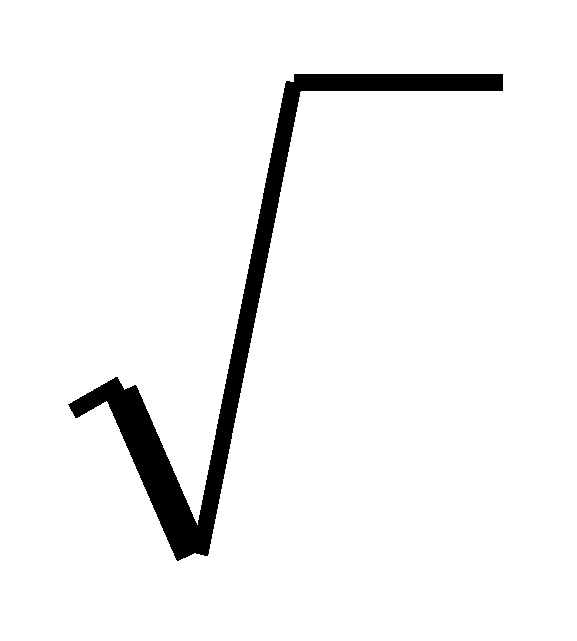 (1-v2/c2))= d(m0v2/ (1-v2/c2))= d(m0v2/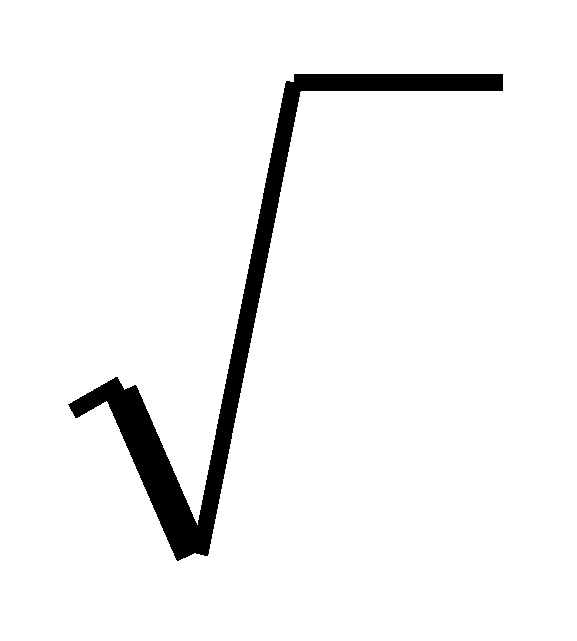 (1-v2/c2))=c2dm; (1-v2/c2))=c2dm;
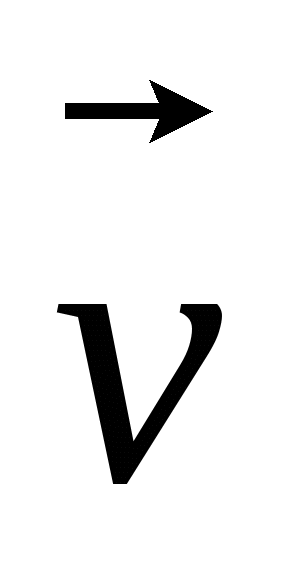 dv=vdv; T=(m-m0)c2 dv=vdv; T=(m-m0)c2
Это справедливо и для полной энергии, т. е. любое изменение массы сопровождается изменением полной энергии.
∆E=∆mc2 ; E=m0c2/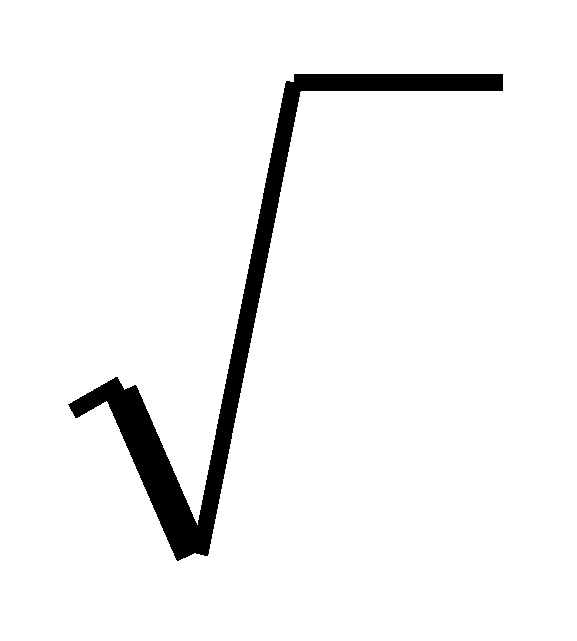 (1-v2/c2); E= m0c2+T (1-v2/c2); E= m0c2+T
Релятивистское соотношение между p и E:
p2c2=T(T+2m0c2)
Эффект Комптона.
При освещении рентгеновскими лучами тонких пластин из металла,угля, парафина, наблюдается рассеивание лучей.
ε=2πЋс/λ; p= Ћω/c
ε=2πЋc/λ; p’= Ћω’/c
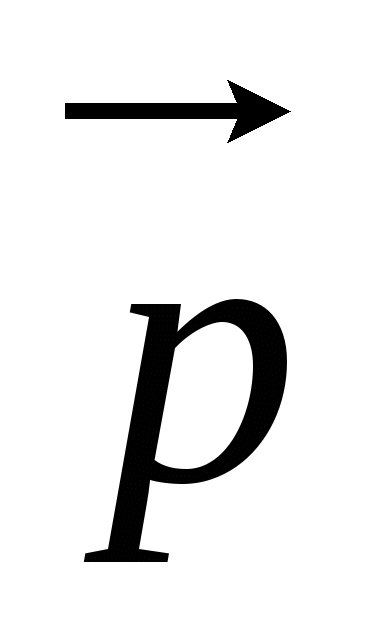 =m =m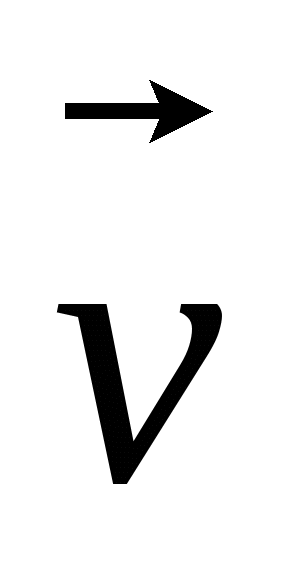
Θ-угол рассеивания
Рассеянные лучи имеют меньшую частоту, которая зависит от угла.
Рассмотрим упругое столкновение.
ε=Ћω=2πЋc/λ; p= Ћω/c: ω=2π/T=2π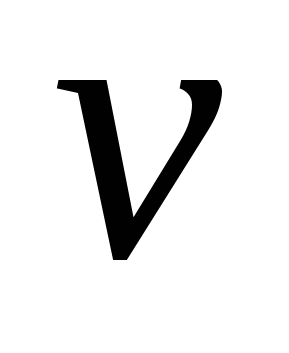 =2πc/λ =2πc/λ
E0=m0c2
Фотон изменяет направление своего движения
ε=Ћω=2πЋc/λ; p’= Ћω’/c; p=mv; E=mc2
Электрон испытывает отдачу
εф+E0=εр.ф.+Е (1)
p=pэ+pф (2)
Тогда Ћω+m0c2= Ћω’+mc2 (3)
m2v2=(Ћω/c)2+(Ћω’/c)2-2Ћωω’/c2 (4)
Возведём (3) в квадрат и вычтем из (4)
m0c2(ω-ω’)=Ћωω’(1-cosΘ)
ω=2πc/λ; ω’=2πc/λ’; ∆λ=λ’-λ
m0c2(2πc/λ-2πc/λ’)=m0c2·2πc((λ’-λ)/ λ’λ)
После приведения к общему знаменателю:
∆λ=2πЋ/m0c(1-cosΘ)=λк·Sin2(Θ/2)
λк=2πЋ/m0c=2,4·10-12 м
Под периодическим действием световых волн электрон излучает волны той же частоты.
Фотоэффект и эффект Комптона обусловили взаимодействие электрона с фотонами. Излучении абсолютно чёрного тела, фотоэффект и эффект Комптона служат доказательством квантового представления света.
Интерференция, дифракция и поляризация подтверждают волновую природу света.
1923 г. Луи Де Бройль сказал, что не только свет проявляет корпускулярные и волновые свойства. Почему частица не может быть волной? Ввёл понятие волны Де Бройля. Он сказал: “Частица- это частица и волна при определённых условиях”. По его предположению частицы могут описываться длиной волны, и эта длина волны связана с корпускулярной характеристикой –импульсом. Соотношение, связывающее между собой корпускулярные свойства частиц: E и p, и волновые: ω и λ:
ε=Ћω; ω=2πc/λ
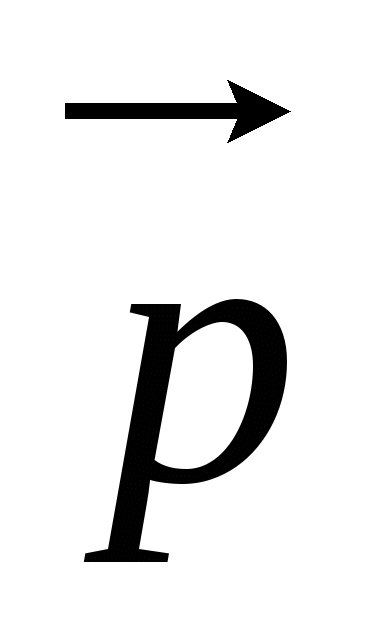 = =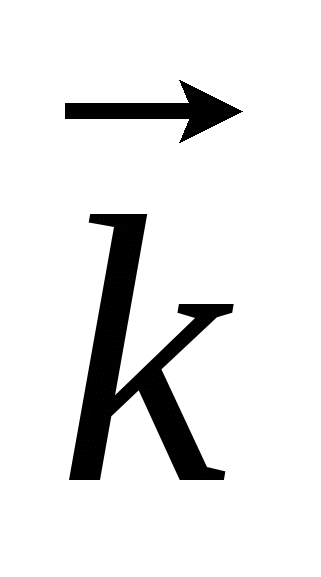 Ћ (k=ω/c), тогда он может предположить , что длина волны может быть описана характеристикой: Ћ (k=ω/c), тогда он может предположить , что длина волны может быть описана характеристикой:
λБ=2πЋ/p=2πЋ/mv -длина волны де Бройля
Дэвисон и Жермен подтвердили идею Де Бройля экспериментально. Они наблюдали дифракцию на кристаллах.
Так был установлен корпускулярно-волновой дуализм: т.е. между микрочастицами и фотонами не существует различия и в зависимости от условий частицы могут проявлять или корпускулярные или волновые свойства. Волны Де Бройля не имеют аналогов в классической физике и тогда можно спросить: что такое электрон- волна или частица?- это и то и другое.
Волны де Бройля имеют универсальную характеристику. Применительно к макротелам они не обнаружены, т.к. если есть m=1 гр, v=1м/с, то λ=10-31 м , что нельзя увидеть.
Соотношение неопределенностей Гейзенберга.
Нельзя приписывать микрочастицам либо все свойства частиц, либо все свойства волны.
Необходимо ввести ограничения к микромиру понятий классической физики. В классической физике каждая частица движется по определённой траектории и в любой момент времени можно точно определить её координату и её импульс (всегда). Микрочастица из-за наличия волновых свойств отличается от классических частиц, и основное различие состоит в том, что нельзя говорить о движении частиц по определённой траектории, а также нельзя одновременно точно определить координату частицы им её импульс.
Понятие длины волны в(0) вообще не имеет смыла. Поэтому частица имея точный импульс, не можнт иметь точной координаты и наоборот.
В 1927 году Гейзенберг ввёл соотношение неопределённостей:
произведение неопределённостей координаты и соответствующей ей проекции импульса не может быть меньше Ћ.
ΔxΔpx≥Ћ
ΔyΔpy≥Ћ
∆z∆pz≥Ћ
Пусть поток электронов проходит через узкую щель величиной ∆x, т.к. электрон обладает волновыми свойствами, то при прохождении через щель, размер которой сопоставим с волной Де Бройля λБ, на экране наблюдается дифракционная картина с главным максимумом. До щели электроны движутся вдоль оси y и проекция их импульса на ось x=0 (px=0 и ∆x=0(до щели)) абсолютно не определена. В момент прохождения щели положение электрона на оси x определяется размером щели ∆x. В этот же момент из-за дифракции электронов они отклоняются на угол 2φ, где φ-угол соответствующий первому дифракционному максимуму на щели. Появляется неопределённость для проекции импульса для оси x.
∆ px=p·Sinφ=(2πЋ/λБ) ·Sinφ
По условию первого дифракционного максимума на щели Δx·Sinφ должен быть равен чётному числу полуволн.
На первом минимуме это λ.
∆x·Sinφ=λ; ∆x= λ/ Sinφ;
Тогда ∆x·∆px= (λ/ Sinφ)·(2πЋ/λБ) ·Sinφ=2πЋ
Существует также другое соотношение:
∆E·∆t≥Ћ
∆E -это неопределённость энергии в системы в момент измерения этой энергии.
∆t -неопределённость длительности процесса измерения.
Система. имеющая время жизни Δt, не может быть охарактеризована определённым значением энергии.
Неопределённость по времени –это то время в течение которого система пребывает в состоянии с неопределённой энергией. Например, испускание телом цуга волн(тогда измерить энергию невозможно).
Оценка с помощью соотношения неопределенностей основного состояния.
Частицы находятся в потенциальной яме шириной L, где она может находиться только во второй области и не может зайти в первую и третью, т.к. яма обладает непроходимыми для частицы стенками( на границах потенциальной ямы U=∞)
∆x=L
Неопределённость по импульсу 100%.
Тогда ΔxΔpx≥Ћ
LΔpx≥Ћ
L2Δpx2≥Ћ2
Δpx=m∆vx=px
L2m2∆vx2≥Ћ2, тогда L2m2vx2≥Ћ2
E=p2/2m
L2(m2∆vx2/2m)≥Ћ2/2m( в скобках энергия)
L2E= Ћ2/2m
E= Ћ2/2mL2-энергия основного состояния
Отсюда следует , что частица, находящаяся в потенциальной яме, никогда не может “лечь” на дно этой ямы, потому что был бы нарушен принцип неопределенностей, в этом случае была бы известна и координата и импульс.
Оценка естественной ширины спектральной линии.
Ширина- это разброс по энергиям.
В не возбужденном состоянии система может находиться в течении времени τ=∞.
В возбужденном состоянии система находится τ=10-8 с.
В соответствии с принципом неопределенностей энергия возбужденного состояния не может быть точно определена и ∆E·∆t≥Ћ всегда остаётся.
Для основного состояния при τ=∞.
∆E0=Ћ/∞=0
поэтому основное состояние- это бесконечно узкий основной уровень.
Для возбужденного состояния:
∆EВ=Ћ/τ=Ћ/10-8= 10-26 Дж = 10-7 Эв
Возбужденное состояние это уже интервал ∆EВ.
∆EВ- ширина спектральной линии.
Оба соотношения Гейзенберга можно приравнять:
∆E·∆t= ΔxΔpx, тогда нас интересует сама ширина спектральной линии по длинам волн.
E=2πЋc/λ
∆E=(-2πЋc/λ2)·∆λ; ∆λ=∆Eλ2/2πЋc(“-” можно убрать)
При λ=600 нм(видимый свет), а ∆E=10-7 Эв, тогда ∆λ=10-4 –такова неточность, такова ширина реально.
Волновая функция и её статистический смысл.
Сравним дифракцию света и дифракцию электронов, дифракционная картина световых волн характеризуется те, что в результате наложения дифрагирующих волн в различных точках пространства происходит усиление или ослабление амплитуды колебаний а интенсивность зависит от А2.
По фотонной теории интенсивность определяется числом фотонов, попадающих в данную точку дифракционной картины, следовательно число фотонов в данной точке картины задаётся квадратом амплитуды световой волны, в то время как для одного фотона А2 определяют вероятность попадания в данную точку.
Дифракция микрочастиц также характеризуется неодинаковым распределением потоков микрочастиц, рассеянных по разным направлениям.
Наличие максимумов в дифракционной картине по волновой теории означает, что это направление соответствует бОльшей интенсивности волн де Бройля, с другой стороны эта интенсивность определяет число частиц, попавших в данную точку, Т.о., дифракционная картина для микрочастиц является проявлением вероятной закономерности. т.е. частицы попадают в те места, где интенсивность волн де Бройля наибольшая. Можно ли считать волны де Бройля -волнами вероятности, т.е. вероятность обнаружить частицу в в различных (0) меняется по волновому закону.
IA2
Если считать волны де Бройля волнами вероятности, то получается, что обнаружить частицу в некоторых точках пространства, т.е. вероятность будет отрицательной . Вероятность не может быть меньше нуля- это не имеет физического смысла.
В 1926 году Макс Борн предложил, что по волновому закону меняется не вероятность , а величина, названная амплитудой вероятности
Ψ(x,y,z)
Эту функцию он назвал “пси-функцией” или волновой функцией. Она может быть действительной величиной, а может быть и мнимой или комплексной и тогда вероятность будет равна квадрату модуля пси-функции.
ω=|Ψ(x,y,z)|2
Вероятность нахождения частицы в данном объёме пространства ∆ω- это квадрат модуля пси-функции, умноженный на объём:
∆ω=|Ψ|2dV
|Ψ|2=dω/dV
|Ψ|2 имеет физический смысл плотности вероятности, т.е. определяет вероятность того, что частица находится в единичном объёме с координатами x,y,z, т.е. физический смысл имеет не сама пси-функция, а квадрат её модуля, которым задаётся интенсивность волн де Бройля. Если за объём V принять объём всего пространства, то необходимо волновую функцию нормировать так, чтобы вероятность достоверного события была равна единице:
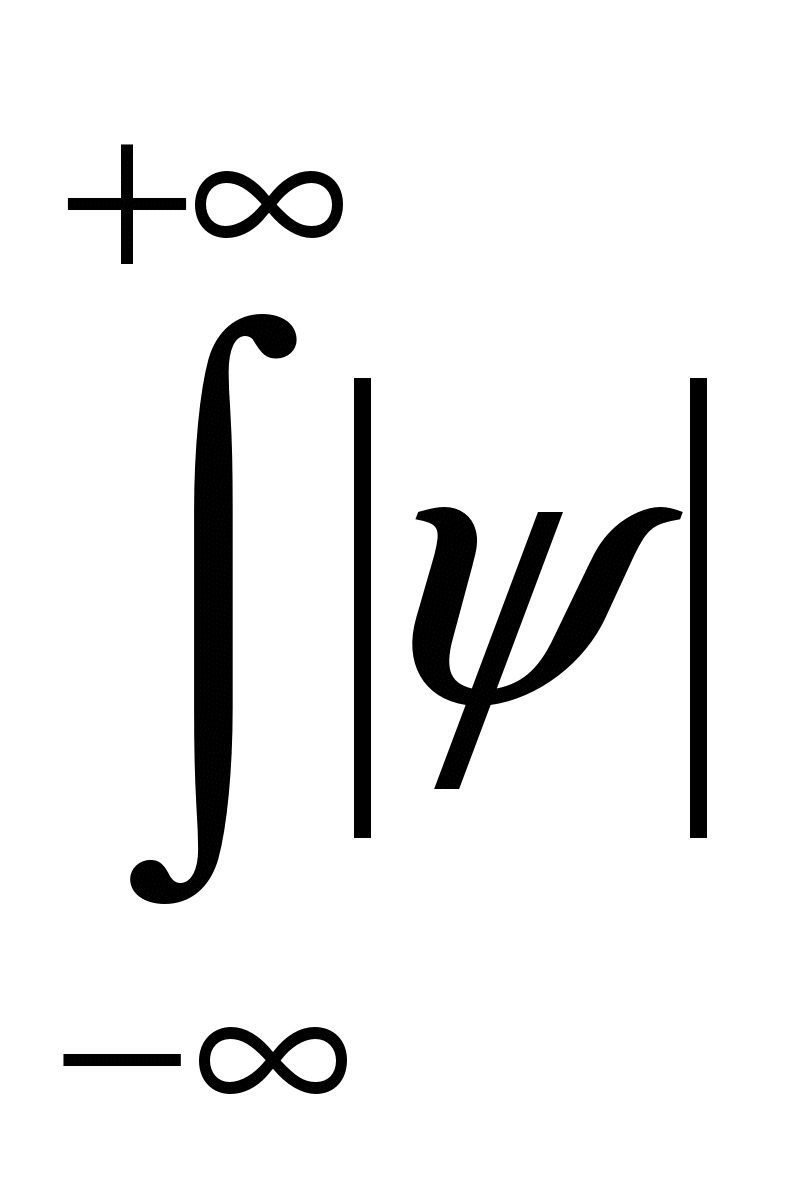 2V=1 2V=1
Пси-функция должна быть нормируема, а также должна удовлетворять следующим условиям:
1)должна быть конечна, так как вероятность не может быть больше 1
2)должна быть однозначна, так как вероятность не может быть неоднозначна
3)должна быть непрерывна, так как вероятность не может изменяться скачком
Уравнение Шредингера.
Ур-е Шр. было придумано.
Статистический смысл волн де Бройля и соотношение неопределенностей Гейзенберга привели к вывожу, что уравнение движения частиц в квантовой механике должно быть волновым.
 2/(2m)·ΔΨ+U(x,y,z,t)Ψ(x,y,z,t)=iЋ·(∂Ψ(x,y,z,t)/∂t (1) 2/(2m)·ΔΨ+U(x,y,z,t)Ψ(x,y,z,t)=iЋ·(∂Ψ(x,y,z,t)/∂t (1)
Это ур-е называется временным уравнением Шредингера.
ΔΨ=∂2Ψ/∂x2+∂Ψ2/∂y2+∂2Ψ/∂z2- оператор Лапласа
U(x,y,z,t)-потенциальная энергия частицы, находящейся в силовом поле
Ψ(x,y,z,t)-искомая волновая функция
Это уравнение справедливо для любых частиц, движущихся со скоростью v<
Это уравнение дополняется следующими условиями:
пси-функция конечна непрерывна однозначна
∂Ψ/∂x, ∂Ψ/∂y, ∂Ψ/∂z, ∂Ψ/∂t должны быть непрерывны тоже
Квадрат модуля пси-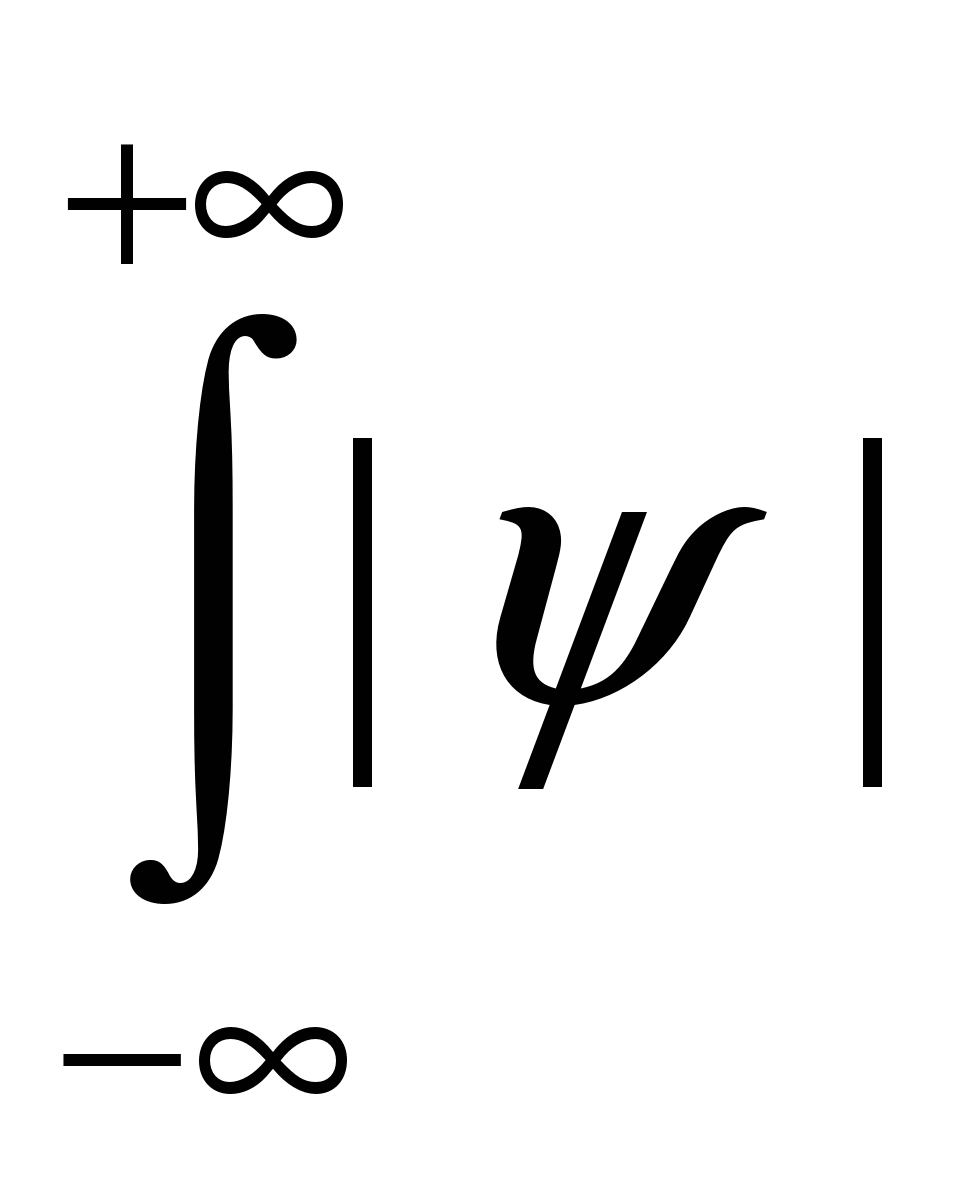 2dV=1функции должен быть интегрируем и должно выполняться условие нормировки 2dV=1функции должен быть интегрируем и должно выполняться условие нормировки
Если пси-функция не зависит от времени, то можно получить стационарное Ур-е Шр.
Перейдём от временного равнения к стационарному и допустим, что есть комплексное число.
в стационарном Ур-и Шр. пси-функция не зависит от времени, а только от координат x,y,z? тогда потенциальная энергия зависит только от координаты.
Решение общего(временного) уравнения может быть представлено в виде произведения двух функций и уравнения плоской волны , которой сопоставима волна де Бройля; может быть написано:
ξ(x,t)=A·Sin(ωt-kx)=A·exp(i(wt-kx))
ω=E/Ћ; k=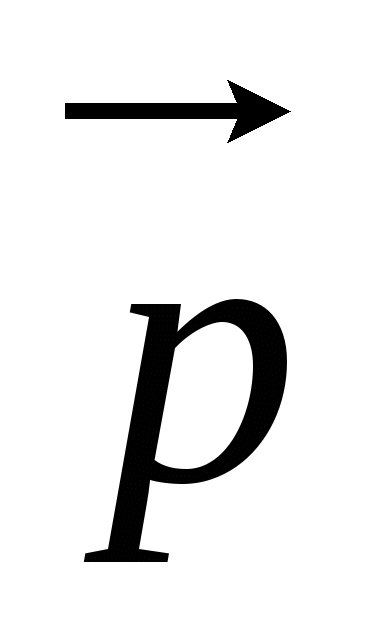 /Ћ /Ћ
Ψ=A·exp(-i/Ћ(Et-px))
В квантовой механике показатель еxp всегда берут со знаком “-”.
Уравнение Шредингера можно упростить исключением времени; т.е. найти уравнение Шредингера для стационарного состояния с фиксированными значениями энергии, это возможно. если силовое поле, в котором движется частица .Тогда решение Ур-я Шр. может быть представлено в в виде функций, одна из которых является только функцией координат, а другая только функцией времени.
Ψ(x,y,z,t)= Ψ(x,y,z,t)·еxp(-Et/Ћ) (2), где Е- полная энергия частицы. Если уравнение (2) после взятия второй производной подставить в уравнение (1), то после сокращения члена Et/Ћ мы получим стационарное уравнение Шредингера:
ΔΨ=(2m/Ћ)(E-U)Ψ=0 (3), где U- потенциальная энергия частицы в поле.
Движение свободной частицы.
Свободная частица-частица, на которую не действуют силы, и в этом случае, её потенциальная энергия принимается равной нулю.
Рассмотрим движение частицы вдоль оси x. Из уравнения (3) исключим потенциальную энергию, и тогда Δ превращается во вторую производную:
d2Ψ/dx2+(2m/Ћ2)·EΨ=0
Ψ2+k2Ψ=0, k2=(2m/Ћ2)·E
Решение этого уравнения может быть представлено в виде:
Ψ=A·exp(kx); E=κ2Ћ2/2m=p2/2m; p=kЋ
Получается, что энергия Е, не квантованная величина и ничем не отличается от энергии неклассической частицы и может принимать любые положительные значения.
|
|
|
 Скачать 0.59 Mb.
Скачать 0.59 Mb.