|
|
Лекции по физике 4 семестр. Фотон обладает массой m
Частица в глубокой одномерной прямоугольной яме с бесконечно высокими стенками.
Если на частицу действует сила, то появляется потенциальная энергия, которая зависит только от координат и при движении частицы эта потенциальная энергия будет меняться, решение Ур-я Шр. в этом случае будет иметь физический смысл не при всяком значении полной энергии, а только при некоторых её дискретных значениях. Значения полной энергии Е, при которых существует решения уравнения Шредингера называется собственными значениями энергии (Еn), а функция Ψ, удовлетворяющая Ур-ю Шр. для данного значения энергии.
Ψ(x,y,z)-собственная функция Ψn.
Частица находится в глубокой прямоугольной яме.
Частица может двигаться только вдоль оси x. Движение частицы ограничено непроходимыми стенками при x=0 и x=l. Стенки непроходимы, т.к. на этих стенках потенциальная энергия принимается, равной бесконечности, и частица, в принципе, не может оказаться в 1 и3 областях.
ω1=ω3=0; Ψ1=Ψ3=0; Ψ2<>0, U2=0
Тогда Ур.-е Шр. для второй области:
d2Ψ/dx2+(2m/Ћ2)EΨ=0 (1)
Тогда обозначим (2m/Ћ2)Е=k2 (2)
Ψ”-k2Ψ’=0 (3)
Решение Ур-я Шр. мы будем искать в тригонометрической форме:
Ψ=с1Sin(kx)+c2cos(kx)
Граничные условия:
Ψ(0)=0 (5)
При подставлении этого граничного условия получаем с2=0:
Ψ=с1Sin(kx)
Второе граничное условие:
Ψ(l)=0
Подставляя получаем:
Ψ=с1Sin(kl)=0 (7)
Это возможно только, когда:
Sinl=0; kl=πn; k=πn/l (8), n=1,2,3,…….
n никогда не равно нулю, потому что:
1.это означало бы, что частицы в яме вовсе нет( по сути она никуда не могла исчезнуть).
2.в этом случае нарушался бы принцип неопределённости Гейзенберга, т.к. это бы означало, что у частицы одновременно определены и координата и импульс., т.е. наложение второго граничного условия(Ψ(l)=0) приводит к тому, что параметр К оказывается квантовым, и мы можем записать: Кn=πl/n (9)в выражение (7):
Ψn=с1Sin((πl/n)x) (10)
И тогда Ψ тоже квантована.
Наложим на уравнение (10)условие нормировки, а именно:
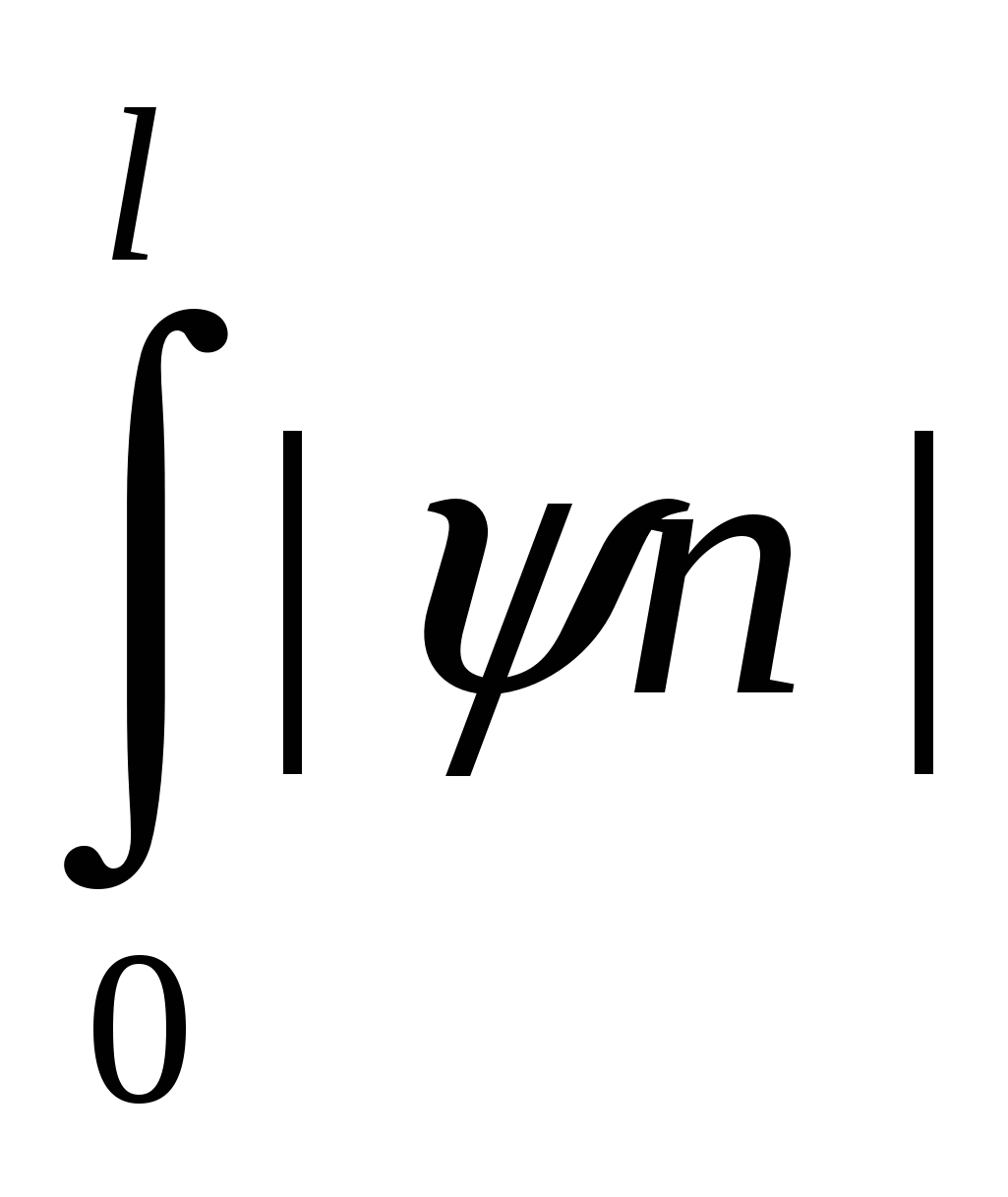 2dx=1 (11) 2dx=1 (11)
Смысл нормировки состоит в том, чтобы найти частицу в пределах ямы с вероятностью 100%. подставим в (11) ур-е ур-е (10)и найдём коэффициент с1.
с12=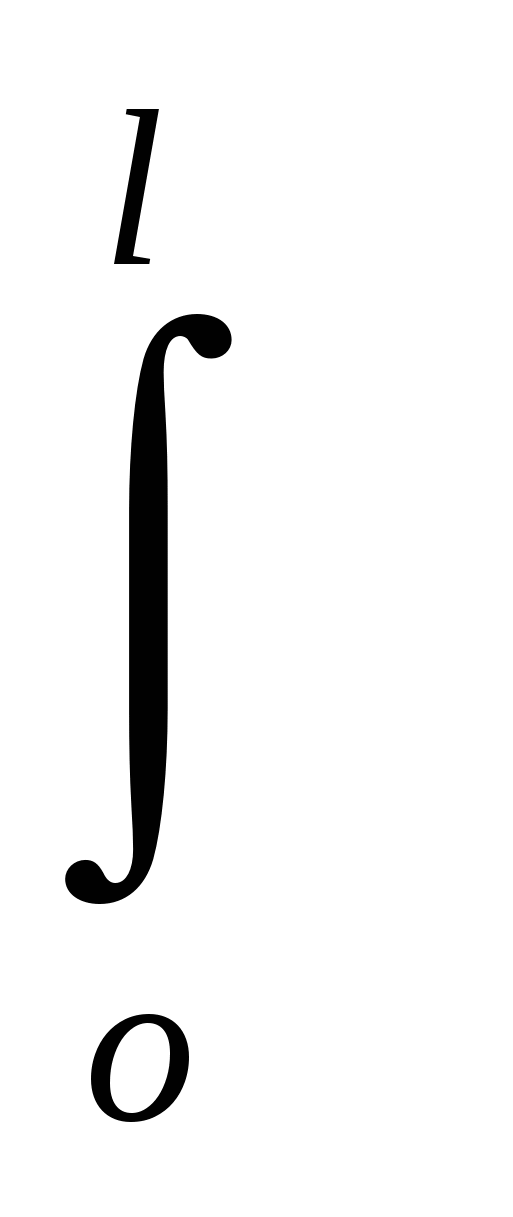 Sin2(πn/l)x)dx=1 Sin2(πn/l)x)dx=1
c12·1/2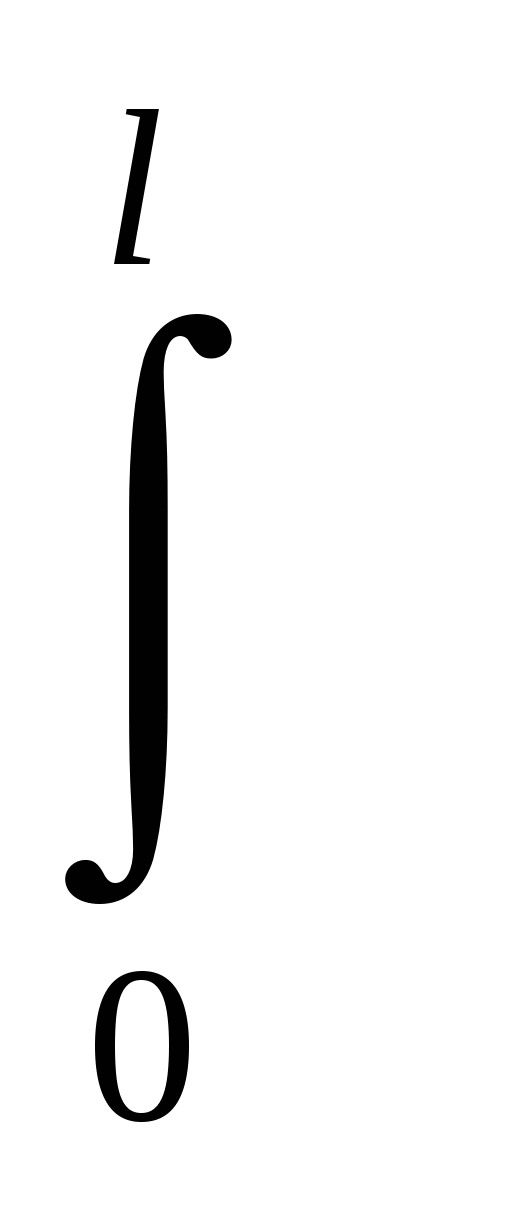 (1-cos((2πn/l)x)dx)=1 (1-cos((2πn/l)x)dx)=1
c12·1/2(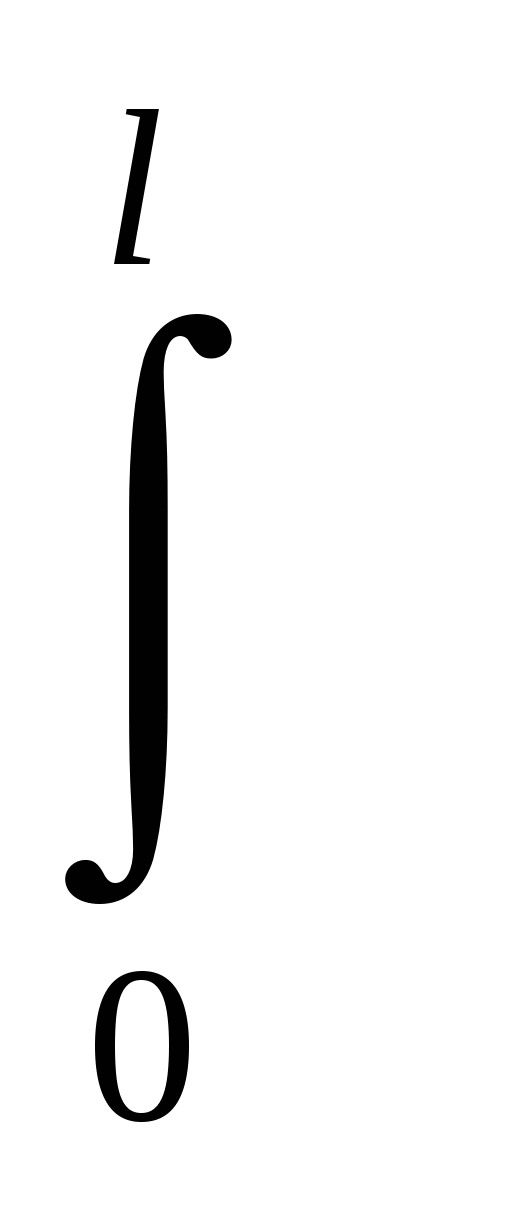 dx- dx-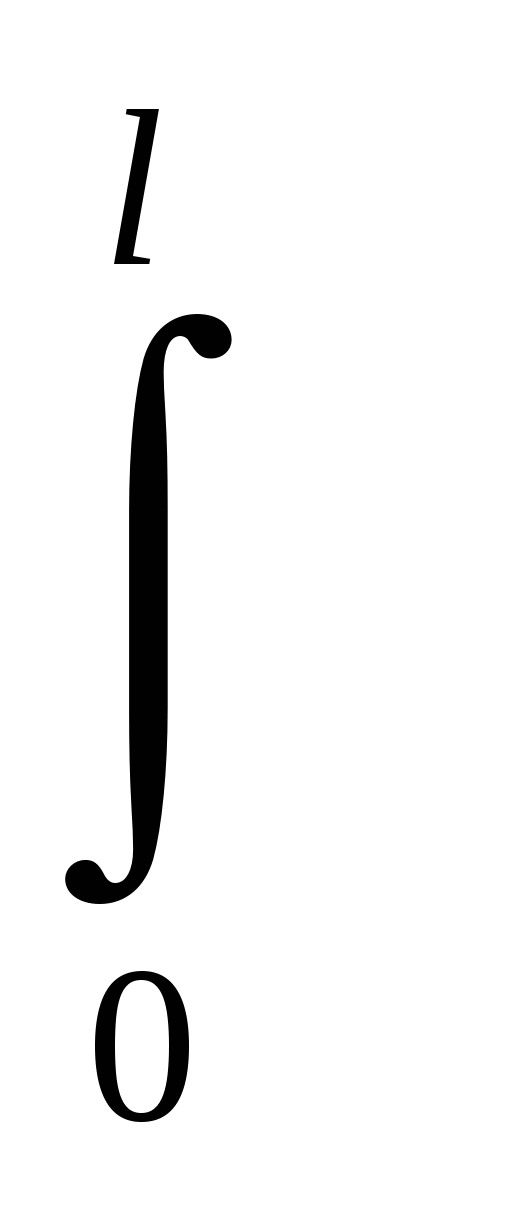 cos((2πn/l)x)dx)=1 cos((2πn/l)x)dx)=1
c12·1/2((l-l/2πn)Sin((2πn/l)x)|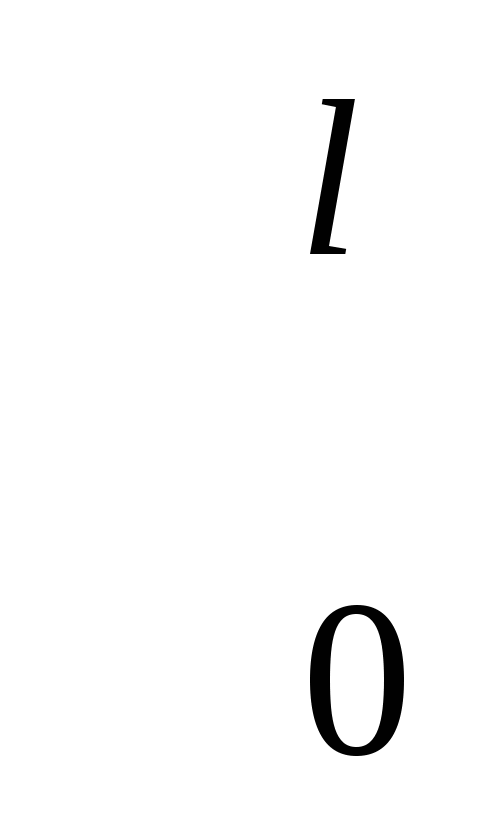 =1 =1
c12·(1/2)l=1
c1=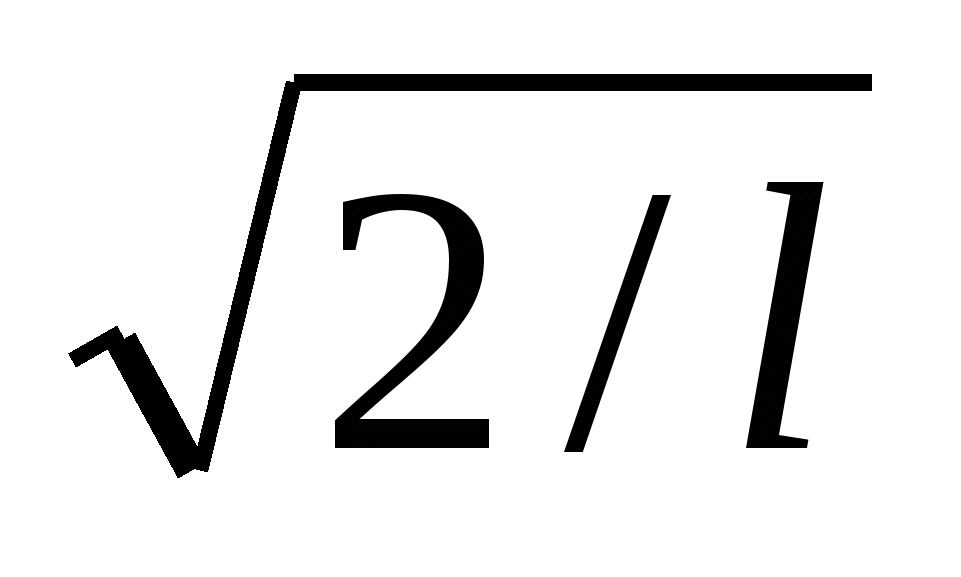
Ψn=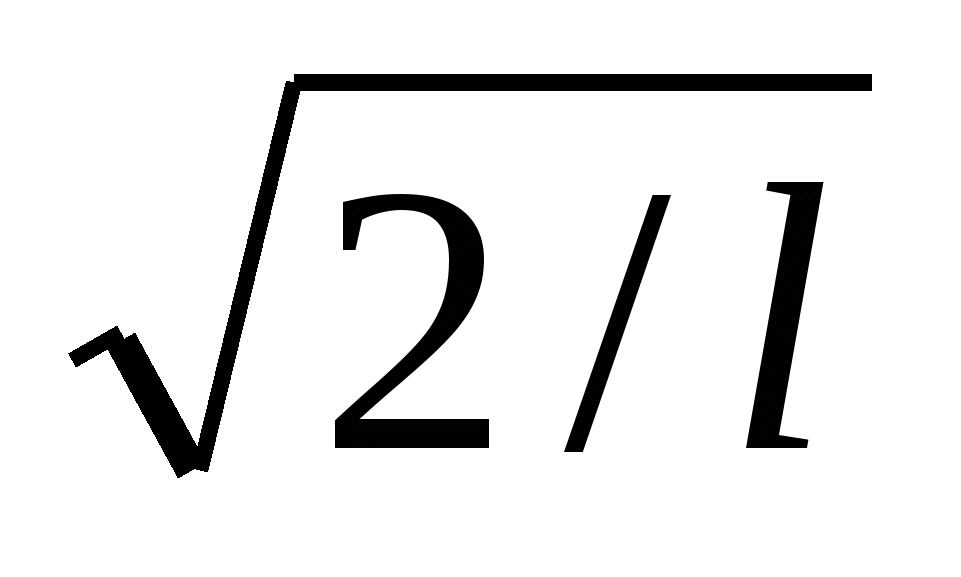 Sin((πl/n)x) (12) Sin((πl/n)x) (12)
Найдём собственные значения энергии Еn.
2mE/Ћ2=K2
Kn=πn/l
2mE/Ћ2= π2n2/l2;
En= π2n2Ћ2/2m l2
Проанализируем полученные результаты:
Ψn=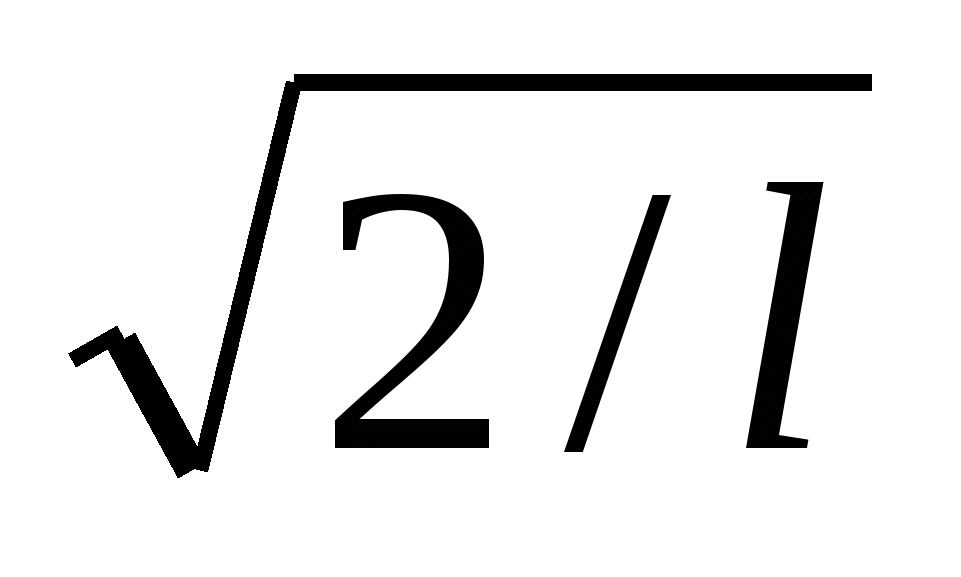 Sin((πl/n)x) Sin((πl/n)x)
En= π2n2Ћ2/2m l2
При большом n вероятность обнаружить частицу в каком-то конкретном месте ямы должен быть равновероятной, что приближается к классической теории.
Частица с n=2 не может быть обнаружена в середине ямы и такое представление не совместимо с классической физикой, потому что в классической физике положение частиц равновероятно.
Принцип соответствия бора.
En= π2n2Ћ2/2m l2
Из этого выражения можно найти энергетический интервал между двумя соседними уровнями.
∆ En=Еn+1- En= π2(n+1)2Ћ2/2m l2- π2n2Ћ2/2m l2= π2(2n+1)Ћ2/2m l2.
На больших n(n >>1):
π2Ћ2/2m l2(2n+1)= π2Ћ2n/m l2
Например для электрона при размерах ямы l=10 см ∆ E=10-35n Дж=10-16n Эв
т.е. энергетические уровни расположены так тесно, что спектр практически непрерывен.
Но если размеры ямы соизмеримы с размерами атомами(l=10-10м), то это значит для электрона ∆ E10-17n Дж=102n Эв, т.е. получается при атомарных размерах l разность энергий между уровнями носит явно дискретный характер. Частица в потенциальной яме с бесконечно высокими стенками не может иметь энергию меньше, чем Е1= π2Ћ2/2m l2(n=1). И это также вытекает из соотношения неопределенностей: ∆x=l и импульс поэтому не может иметь точного значения, а именно он не может иметь значения ноль.
Такому разбросу импульса соответствует энергия Emin=∆p2/2m=Ћ2/2m l2
∆p/∆x≥Ћ; ∆p=Ћ/∆x=Ћ/l
Все остальные уровни при n>1 имеют большую энергию и при n>>1 отношение ∆ En/ En будет выглядеть так:
∆ En/ En=π2Ћ2nml2/ml2π2Ћ2n2
2/n2<<1, т.е. соседние уровни при возрастании располагаются настолько тесно и тем теснее чем больше n. И при очень больших значениях n соседние уровни практически сливаются и дискретность исчезает. И это следствие из принципа соответствия Бора: законы квантовой механики при больших значениях n энергетические законы квантовой физики переходят в законы классической физики.
Квантовое число n определяется как главное квантовое число и по нему всегда можно судить о энергетическом уровне электрона в атоме. Когда n велико, электрон может покинуть атом, перейдя на внешнюю валентную оболочку. Примером частицы в глубокой потенциальной яме может служить электрон, который находится на внутренних оболочках атома.
Потенциальная ступень.
Потенциальной ступенью называется ограниченная параллельными плоскостями область пространства, в которой потенциальная функция U(x) больше, чем в прилегающих областях.
Рассмотрим поведение частицы на границе областей 1 и 2, где потенциальная функция меняется скачком, примем U1=0 и U2=U0.
Рассмотрим случай когда E> U0
по классической физике частица пролетит, а в квантовой физике возможны варианты.
Для каждой области 1 и2 составим уравнения Шредингера(одномерное):
d2Ψ1/dx2+(2m/Ћ2)EΨ1=0
d2Ψ2/dx2+(2m/Ћ2)(E-U)Ψ2=0
Обозначим (2m/Ћ2)Е=k2, тогда
K1=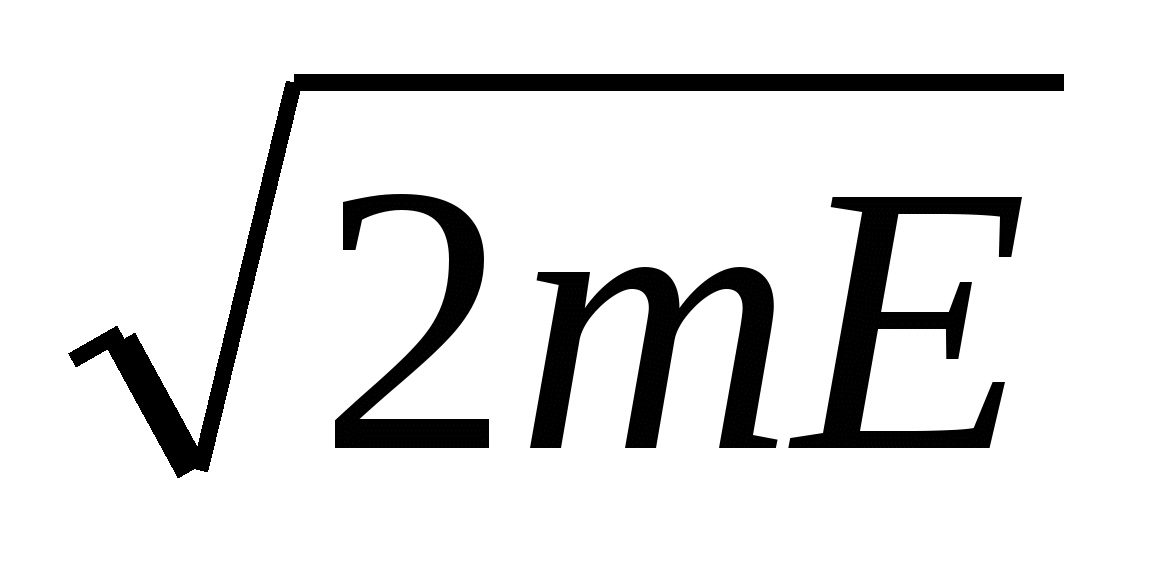 /Ћ=p/Ћ=2π/λ1, где λ1- длина волны де Бройля в 1ой области. /Ћ=p/Ћ=2π/λ1, где λ1- длина волны де Бройля в 1ой области.
К2=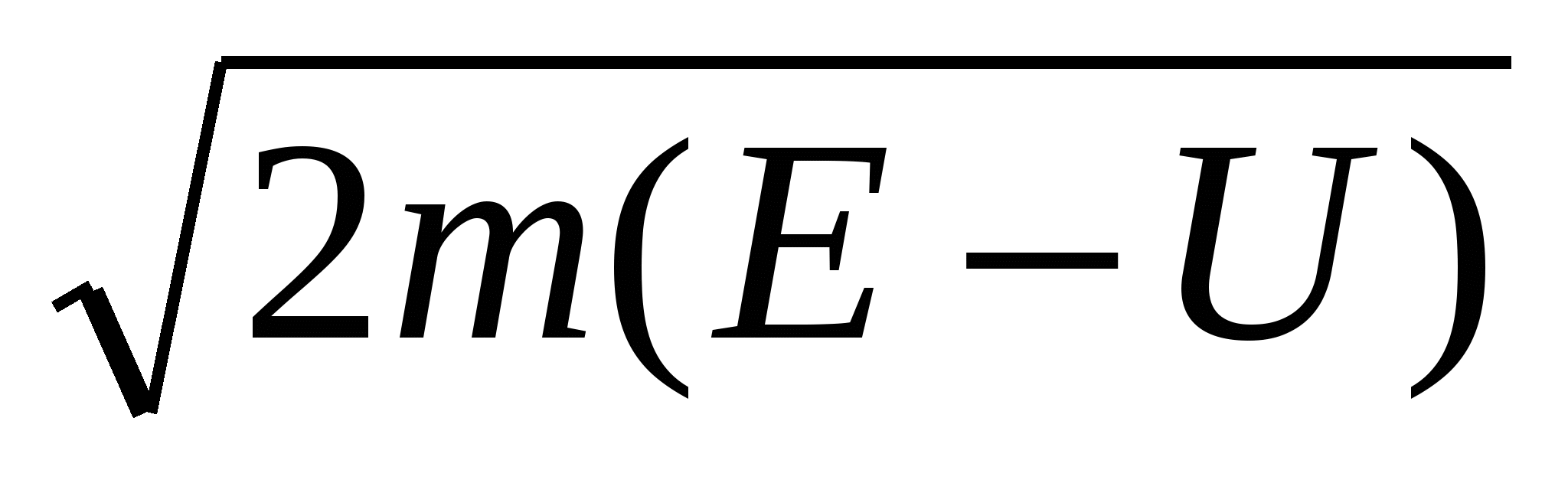 /Ћ=p/Ћ=2π/λ2, где λ2- длина волны де Бройля во второй области. /Ћ=p/Ћ=2π/λ2, где λ2- длина волны де Бройля во второй области.
Ψ1”-k2Ψ1=0 (3)
Ψ2”-k2Ψ2=0 (4)
Решение уравнения Шредингера (3)и (4) будем искать в показательной форме.
Ψ1=A1exp(ik1x)+B1exp(-ik1x)
Ψ2=A2exp(ik2x)+B2exp(-ik2x), где
A1-это амплитуда падающей на ступень волны,
В1-это амплитуда отраженной от ступени волны,
А2-это амплитуда, прошедшей через ступень волны,
В2=0, т.к. не будет отражения
exp(ikx) принадлежит проходящей волне
exp(-ikx) принадлежит отраженной волне
Тогда движение электрона представляется плоской волной де Бройля на границе ступени. где происходит внезапный рост потенциальной энергии эта волна должна вести себя так как ведёт себя световая волна на границе двух сред с различными показателями преломления, следовательно на границе волна де Бройля частично отражается в первую область, а частично проходит во вторую область. Найдём вероятность, с которой волна отразится и вероятность, с которой волна будет проходить.
Для решения этих задач необходимо воспользоваться свойствами волн де Бройля и свойствами волновой функции. при которой функция на границе двух сред непрерывна, а также непрерывна её первая производная .
На границе двух сред функция непрерывна, значит в 1ой области x<0, а во второй области x>0. В т.0 функция должна быть непрерывна и мы получаем:
А1+В1=А2
должны быть равны ещё и первые производные в т. x=0 возьмём первую производную по (3) и (4), подставляем x=0 и получим:
K1(1-B1)=K2A2
получаем систему:
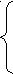 А1+В1=А2 А1+В1=А2
K1(1-B1)=K2A2
Принято А1 принимать равным 1, тогда
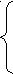
1+В1=А2
K1-К1B1=K2A2
В1=(K1-K2)/(K1+K2)
A2=2K1/(K1+K2)
Пользуясь аналогией с оптикой, определим коэффициент отражения ρ и коэффициент прохождения(прозрачности)
ρ=отношение квадратов амплитуд отраженной и падающей волн:
ρ=B12/A12
 = отношение квадратов амплитуд прошедшей и падающей волны = отношение квадратов амплитуд прошедшей и падающей волны
 =A22/A12 =A22/A12
Получаем ρ=(K1-K2)2/(K1+K2)2
 =4K1K2/(K1+K2)2 =4K1K2/(K1+K2)2
По закону сохранения вещества ρ+ =1 =1
По законам классической физики электрон пройдёт, а в квантовой физике есть вероятность. что электрон будет отражён.
Потенциальный барьер конечной ширины.
В классической физике частица пролететь не может, а в квантовой есть вероятность, что электрон окажется в области 2.
E
Вероятность прохождения частицы через барьер (или прозрачность барьера(D)) определяется отношением вероятности обнаружить частицу в точке x=d за барьером к вероятности в точке x=0 перед барьером:
ω=dω3(d)/dω1(0)
dω1(0)=|Ψ1(0)|2dx
dω3(d)= |Ψ3(d)|2dx
ω=|Ψ3(d)|2dx/|Ψ1(0)|2dx=|Ψ3(d)|2/|Ψ1(0)|2
т.е. задача сводится к нахождению волновых функций 1 и 3. Для каждой из областей запишем своё уравнение Шредингера:
1) d2Ψ1/dx2+(2m/Ћ2)EΨ1=0
d2Ψ2/dx2+(2m/Ћ2)(E-U0)Ψ2=0 - во второй области есть сначала потенциальная энергия.
d2Ψ3/dx2+(2m/Ћ2)EΨ3=0
Введём обозначения К1 и К2:
K1=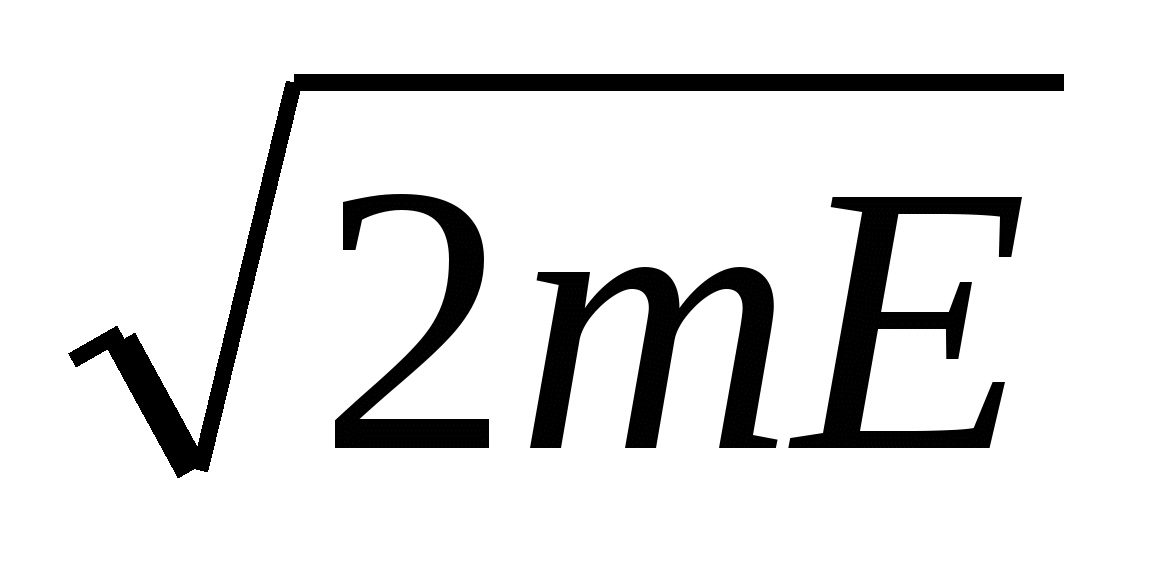 /Ћ /Ћ
К2=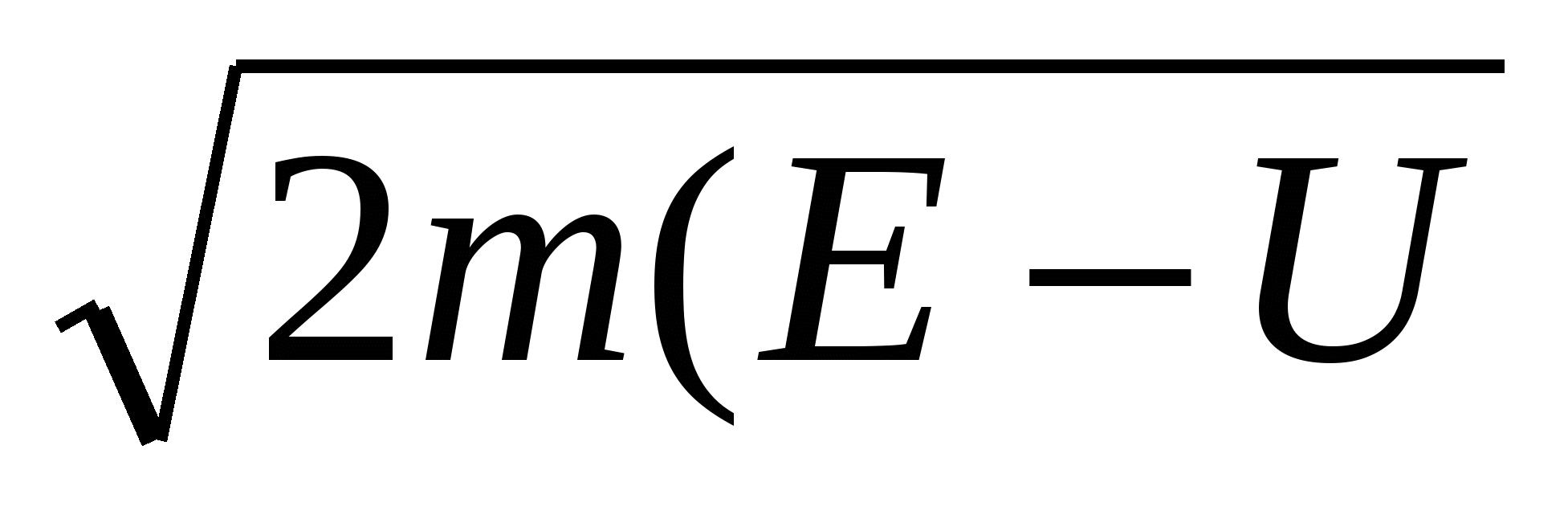 0)/Ћ 0)/Ћ
K3=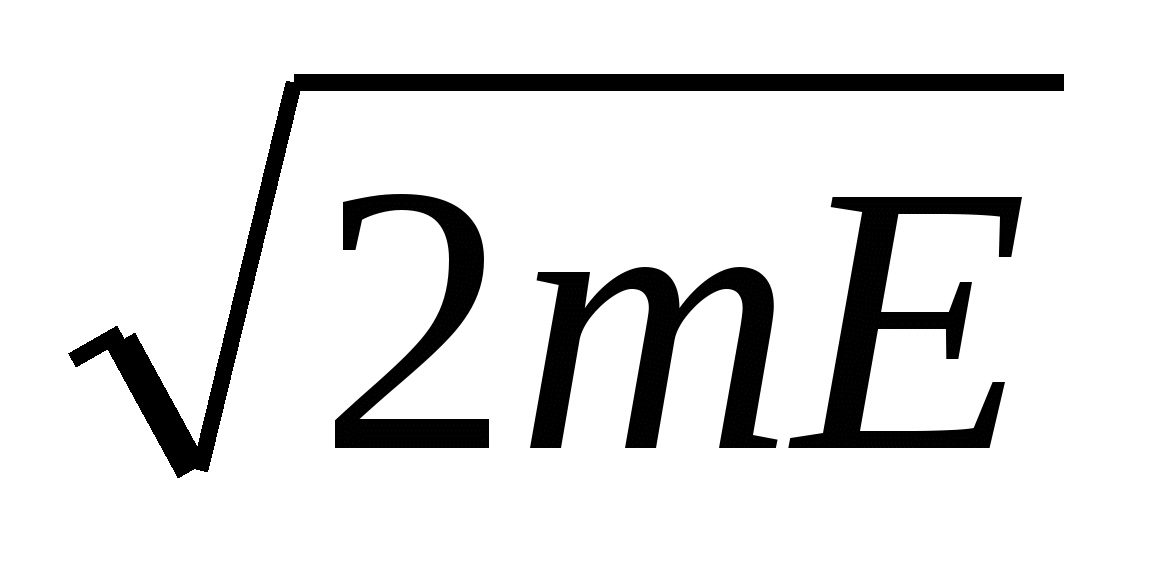 /Ћ /Ћ
Исходные уравнения запишутся в виде:
Ψ1”+k2Ψ1=0
Ψ2”-k2Ψ2=0
Ψ3”+k2Ψ3=0
Решение этих уравнений будем искать в показательной форме:
Ψ1=A1exp(ik1x)+B1exp(-ik1x)
Ψ2=A2exp(-ik2x)+B2exp(+ik2x),
Ψ3=A3exp(ik3x)+B3exp(-ik3x)
exp(ikx) соответствует волне, распространяющейся в положительном направлении оси x
exp(-ikx) в противоположном направлении
А1-амплитуда волны падающей справа на барьер
В1-амплитуда волны, прошедшей через барьер в третью область
В2-амплитуда волны, отраженной от барьера в точке x=d
A3-амплитуда волны, прошедшей через барьер в точке x=d
В3=0 (т.к. как ничего не отражалось)
Не будем учитывать отраженные волны, тогда пси-функции упрощаются:
Ψ1=A1exp(ik1x)
Ψ2=A2exp(-ik2x)
Ψ3=A3exp(ik3x)
Здесь пси-функции содержат мнимую единицу. Вспомним что |Ψ|2=Ψ·Ψ*
|Ψ1|2= A1exp(ik1x)· A1exp(-ik1x)=A12
|Ψ3|2= A3exp(ik3x)· A3exp(-ik3x)=A32
тогда ω= A32/ A12
В области барьера пси-функция действительна, учтём непрерывность пси-функции на границе, тогда в точке x=0 А1≈А2и в точке x=d А3=А2·exp(-K2d), тогда
ω= A32/ A12= А2·exp(-K2d)/ А2= exp(-K2d)
Вспомним, что К2=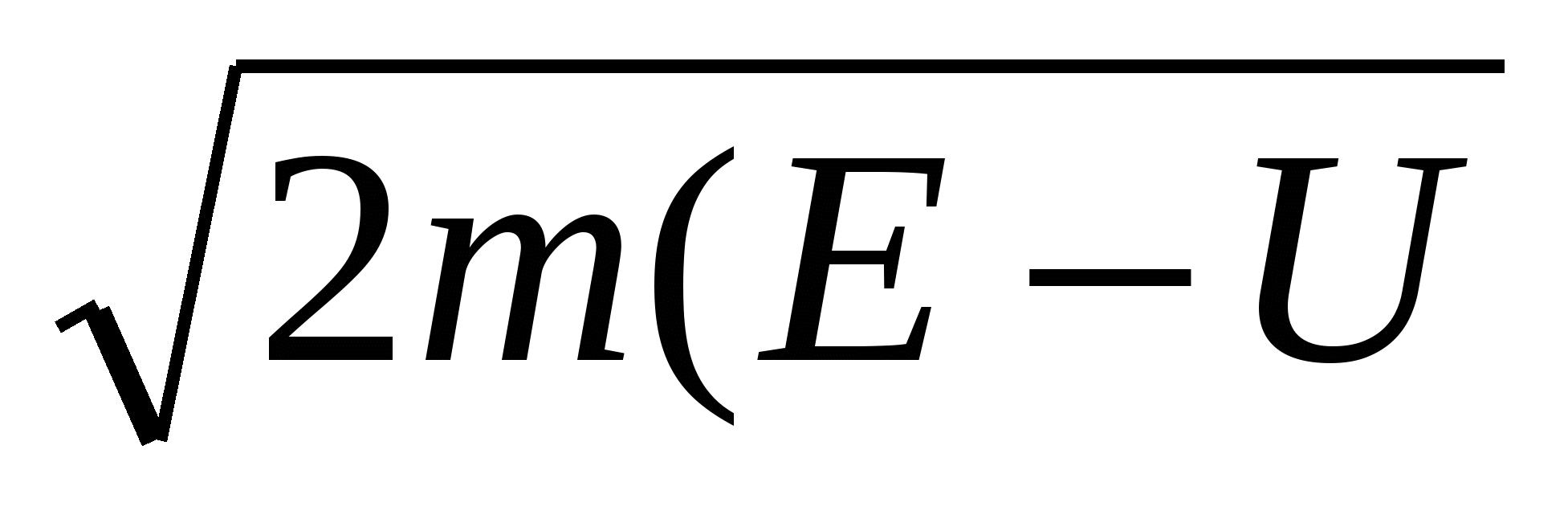 0)/Ћ, тогда 0)/Ћ, тогда
ω=exp((-2/Ћ)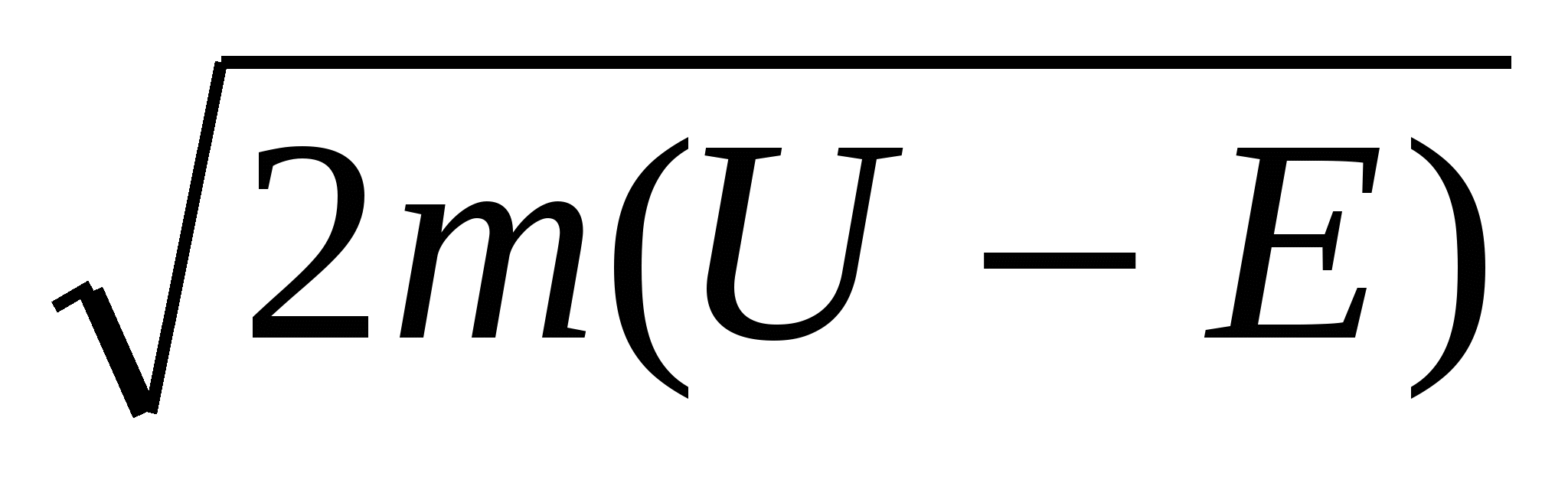 d) d)
Все химические реакции основаны на преодолении потенциального барьера.
Линейный квантовый гармонический осциллятор.
Осциллятор представляет собой материальную точку, которая может совершать гармонические колебания в одном направлении под действием квазиупругой силы F= -βx.
β-отклонение от положения равновесия
F= -dU/dx
dU= βxdx; U=(1/2)βx2
Период тоже умели находить:
T=2π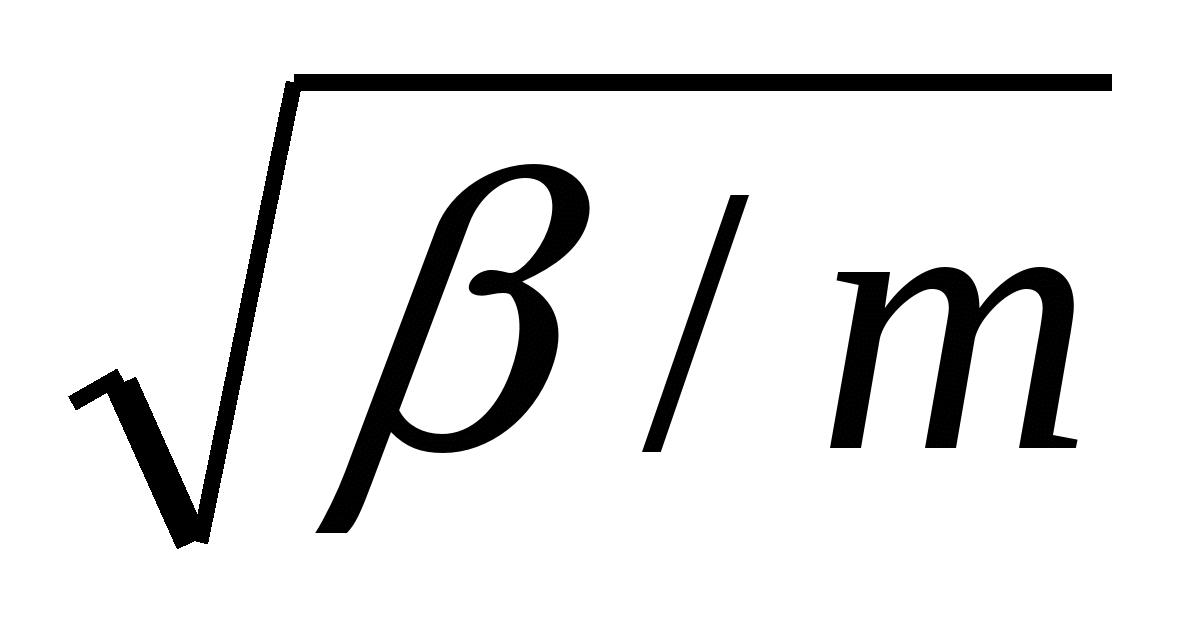 , где ω= , где ω=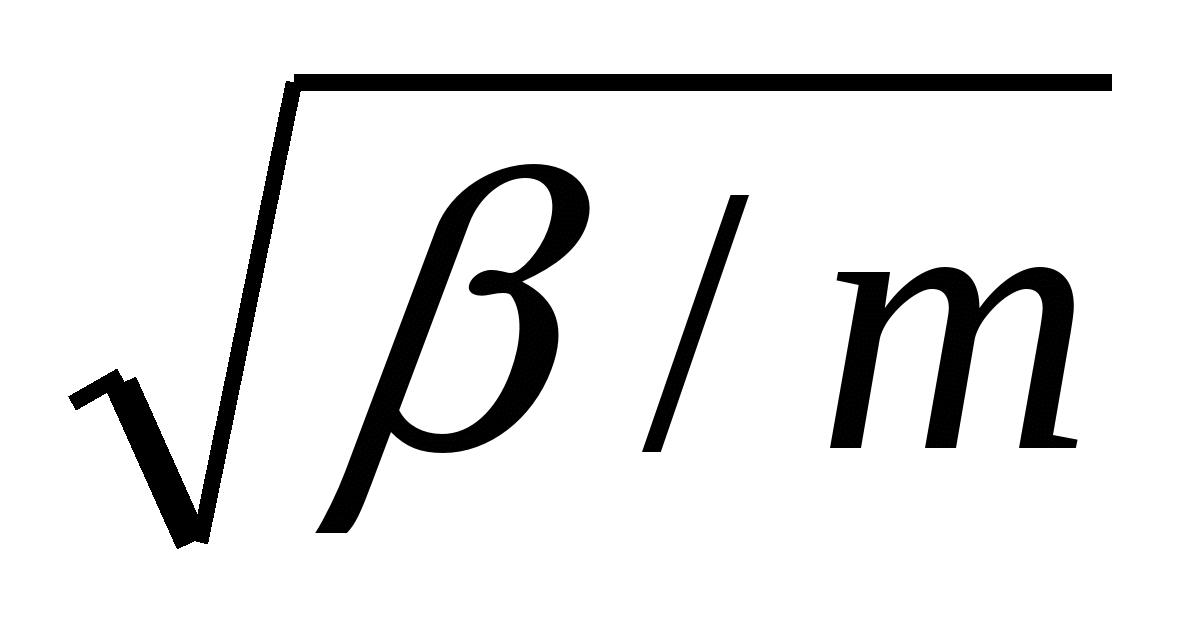 - из уравнения гармонических колебаний. - из уравнения гармонических колебаний.
Когда рассматриваем молекулу как осциллятор массу m заменяем на приведенную массу μ :
μ=m1·m2/(m1+m2)
ω=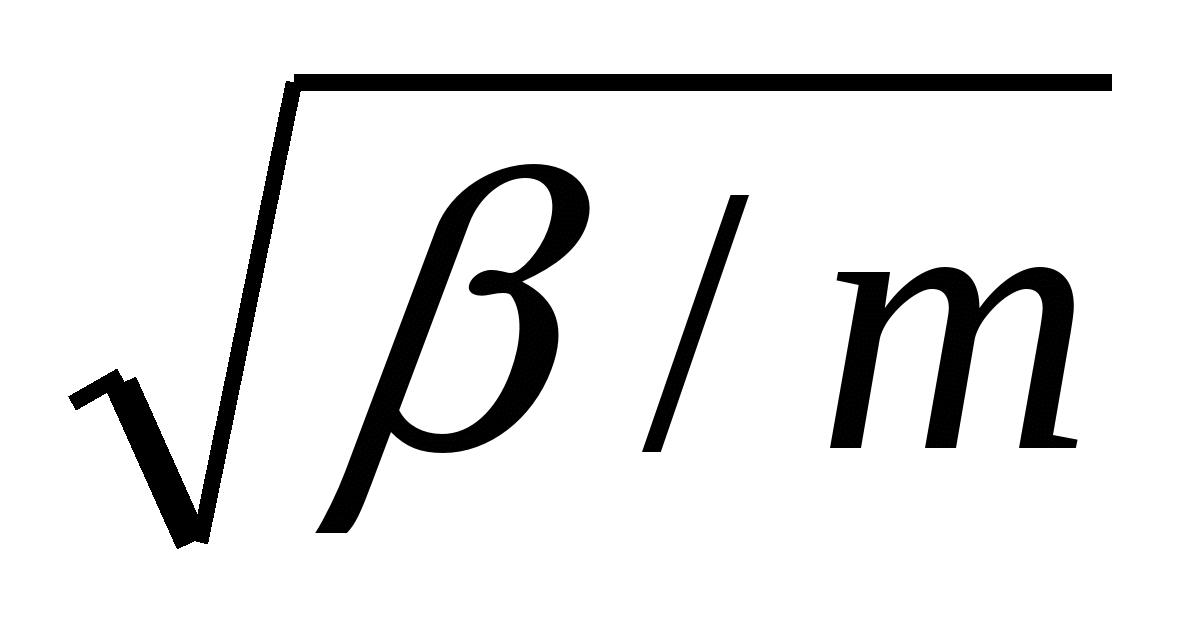 ; β=μω2 ; β=μω2
В квантовом осцилляторе в отличии от классического осциллятора масса очень мала и область движения очень мала, тогда пользуясь формулой для потенциальной энергии:
U(x)=(1/2)· μω2x2
Напишем уравнение Шредингера:
Ψ”(x)+(2μ/Ћ2)·(E-(1/2)· μω2x2)Ψ(x)=0 (*)
Обозначим через α=(2μ/Ћ2)·E и через γ=ωμ/Ћ, тогда:
Тогда (*) перепишется
Ψ”(x)+(α-γ2x2)Ψ(x)=0 (!)
Обозначим через ξ=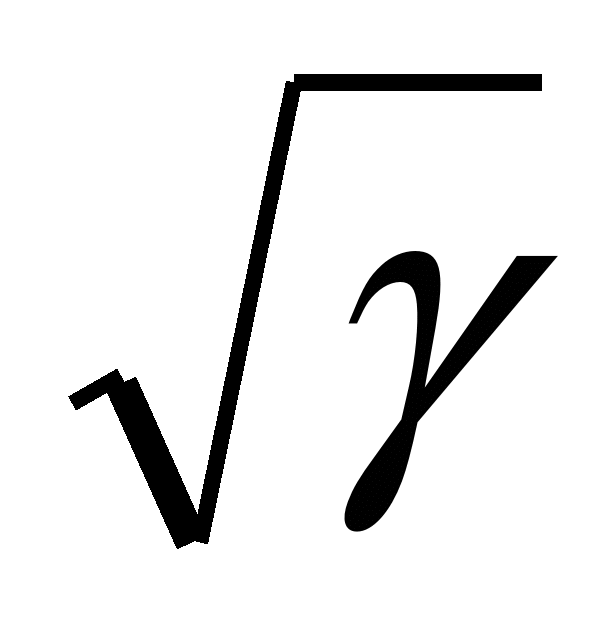 x, тогда γ2x2= ξ2 γ x, тогда γ2x2= ξ2 γ
Перейдём к новой переменной ξ для этого сделаем такое преобразование:
(dΨ(x)/dξ)·(dξ/dx)=ψ’(ξ)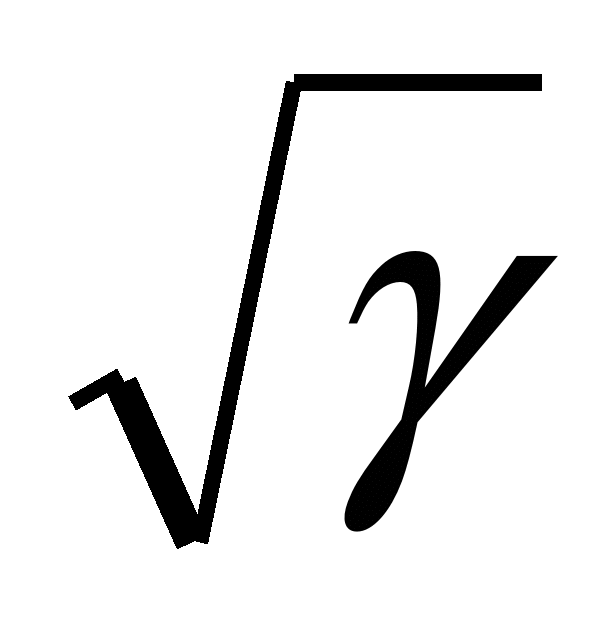
Тогда можно сделать ещё одно преобразование:
Ψ”(x)=γΨ”(ξ)- это подставим в (!):
γΨ”(ξ)+(α-γξ2)Ψ(ξ)=0
Ψ”(ξ)+(α/γ-ξ2)Ψ(ξ)=0 -это диф. ур-е имеет решение только при значениях
α/γ=2n+1, где n=0,1,2,…..
тогда выражение для колебательной энергии будет равняться:
En=Ћω(n+1/2), т.е. при n=0 частица всегда обладает энергией E0=Ћω/2 и это не просто так
Даже при абсолютном нуле частицы не могут покоиться, а колеблются с , т.е. если есть молекула, у которой есть колебательные степени свободы, то при очень низких температурах всегда будет колебательное движение, а поступательного может не быть.
En- для квантового гармонического осциллятора, где n-квантовое число гармонического осциллятора.
Существование нулевой энергии – есть чисто квантовый эффект, и является следствием соотношения неопределённостей. Потенциальная и кинетическая энергия не могут одновременно обращаться в ноль, потому что в противном случае обращались в нуль импульс и координата, что запрещено соотношением неопределённостей.
Из графика видно, что существует возможность, отличная от нуля обнаружить молекулу как гармонический осциллятор в области, заходящую за классическую параболу( это классически запрещенная область). Энергетический спектр гармонического осциллятора дискретен:E=Ћω(n+1/2) и для квантового гармонического осциллятора существует правило отбора, согласно которому ∆n=±1 , и это значит, что все энергетические переходы в квантовом гармоническом осцилляторе осуществляются только между соседними уровнями.
|
|
|
 Скачать 0.59 Mb.
Скачать 0.59 Mb.
 А1+В1=А2
А1+В1=А2