Лекции по физике 4 семестр. Фотон обладает массой m

• Название: Фотон обладает массой m
• Анкор: Лекции по физике 4 семестр.doc
• Дата: 23.04.2018
• Размер: 0.59 Mb.
• Имя файла: Лекции по физике 4 семестр.doc
• Тип: Документы; #18415
• Категория: Физика
• страница: 3 из 7

Потенциал Морзе.

Колебательный энергетический спектр ангармонического осциллятора.

Модель ангармонического осциллятора описывает колебания двухатомной молекулы только при очень малых смещениях x=r-r₀. Согласно модели г.о. с ростом x, F и U неограниченно растут(U=(1/2)·βx², что не может быть в реальности, потому что при смещении молекулы могут расходиться. Это означает, что сила упругости должна описываться более сложной формой кривой, чем парабола. В общем случае колебания молекулы должны быть ангармоническими, а потенциальная энергия должна иметь более сложную зависимость от координаты. Один из самых возможных способов описания потенциальной энергии ангармонического осциллятора(АГО) является потенциал Морзе, по которому: U(r) =U₀[1-exp(-[α(r-r₀)]²

U₀-толщина потенциальной ямы.

r-текущее расстояние между двумя атомами

r₀-расстояние между атомами в момент взаимодействия.

α-коэффициент, характеризующий упругую часть взаимодействия

В п.М. за ноль потенциальной энергии принимается энергия атомов, находящихся на расстоянии .

В случае малых отклонений функция Морзе переходит в обычную параболу, т.е. даёт простую квадратичную зависимость от. Для получения собственных значений колебательной энергии АГО следует в Ур-е Шр. подставить п.М. и мы получаем:

Ψ”(r)+(2μ/Ћ2)(E-U(r))·Ψ(r)=0, где

μ –приведённая масса двухатомной молекулы μ=m₁·m₂/(m₁+m₂)

Решение этого уравнения для ГO даёт значение колебательной энергии:

E_ν=Ћω[(ν+1/2)-γ(ν+1/2)²], где

ω -собственная частота колебаний молекулы,

ν-колебательное квантовое число

γ-коэффициент ангармоничности

Правило отбора для АГО не существует, и поэтому возможны переходы между любыми уровнями.

γ<<1

Для двух соседних колебательных уровней:

∆E_ν+1,ν=E _ν+1-E _ν=Ћω[1-2γ(ν+1)]

С ростом ν расстояние между соседними уровнями уменьшается и при некоторой величине ν_max это расстояние обращается в ноль.

Найдём ν_max:

∆E_ν+1,ν =0

ν_max=1/2γ-1≈1/2γ

этому максимальному колебательному числу соответствует максимальная энергия, которую можно получить, если подставить полученное значение в формулу для энергии E _ν :

E_max=Ћω/4γ

Чисто колебательный спектр излучения молекул состоит из системы линий, частоты излучения ω которых:

Ћω_излуч. = ∆E_ν+1,ν; ω_излуч.=ω(1-2γ(ν+1)), где

ω-собственная частота колебаний молекулы.

Энергия диссоциации равна той энергии, которую необходимо совершить молекуле, находящейся в связанном состоянии, чтобы она диссоциировала на атомы.

D= Ћω/4γ-Ћω/2

Уравнение Шредингера для жёсткого ротатора.

Жёсткий ротатор (ЖР)- материальная точка, которая вращается в пространстве вокруг неподвижного центра, находясь от оси на неизменном расстоянии. В частности эта точка может двигаться по окружности. Система- двухатомная молекула- тоже ЖР.
μ=m₁·m₂/(m₁+m₂)

d-межъядерное расстояние

Эта система характеризуется моментом импульса: ||=μd²ω,

где μd² –момент инерции относительно точки.

Если m₁ и m₂, а также расстояние между ними d являются величинами атомных размеров, то движение ЖР должно описываться квантовыми законами, т.е. Ур-ем Шр. В квантовой механике одновременно могут определены только 2 величины:L² и L_z (проекция момента импульса на выделенное направление), 2 других проекции L_y и L_x не определены, что следует из соотношения неопределённостей. Найдём собственные значения проекций импульса, для этого введём сферические координаты:

r,ν,φ

Δ(x,y,z)Ψ+(2m/Ћ²)(E-U(x,y,z))Ψ(x,y,z)=0

Для перехода в сферические координаты:

x,y,z→ r,ν,φ

x=r·Sinν·Cosφ

y=r·Sinν·Sinφ

z=r·Cosν

Уравнение Шр. в сферических координатах:

(1/r²)[r²(∂/∂r)(r²∂Ψ/∂r)+(∂/∂ν)(Sinν∂Ψ/∂ν)+(1/sin²ν)((∂²Ψ/∂φ²)]+(2μ/Ћ²)(E-U(r))Ψ(r,ν,φ)=0

Для ЖР выполняется ряд условий:

1. 
   т.к. ротатор жёсткий, то r=d
   
2. 
   т.к. ||=const и существует определённое значение L_z , то ν=const →∂Ψ/∂ν=0
   
3. 
   потенциальная энергия из-за отсутствия внешнего силового поля может быть принята равной нулю U=const→ U=0
   

Т.о., при выполнении трёх этих условий Ур-е Шр. сильно упрощается и получается:

(1/r²· sin²ν)(∂²Ψ/∂φ²)+(2μ/Ћ²)EΨ(φ)=0

E=L²/2μd² (E=p²/2m)

L_z=L·cos(90º-ν)=L·Sinν

(∂²Ψ/∂φ²)+ (2μ/Ћ²)( L²/2μd²)·r²·Sin²νΨ(φ)=0

L²Sin²ν= L_z², r=d

Ψ”+ (L_z²/Ћ²)Ψ(φ)=0

Полученное уравнение позволяет определить собственные значения проекций момента импульса, и это уравнение Ψ”+ K²Ψ(φ)=0, позволяет искать решение в следующем виде:

Ψ(φ)=c₁·exp(ikφ)+c₂·exp(-ikφ), k= L_z/Ћ;

Первый член этого уравнения c₁·exp(ikφ) описывает волну, бегущую в “+” направлении угла, второй член c₂·exp(-ikφ)- волну, бегущую в противоположном направлении.

Мы можем ограничиться первым членом, потому что это не изменяет сущности решения:

Ψ(φ)=c₁·exp(i(L_z/Ћ)φ)

Из соображений однозначности пси-функции следует, что exp(i(L_z/Ћ)φ) должна быть равна exp(i(L_z/Ћ)(φ+2π)

Отсюда мы можем получить, что exp(i(L_z/Ћ)2π)=1

используем формулу Эйлера для записи показательной функции exp(i(L_z/Ћ)2π)=cos(L_z/Ћ)2π+i·Sin(L_z/Ћ)2π

Отсюда мы можем найти, что cos(L_z/Ћ)2π=1

Это означает, что (L_z/Ћ)2π=2πm;

L_z=mЋ, где m–квантовое число. которое может принимать значения 0;±1;±2.

Это означает, что проекция момента импульса на заданное направление квантуется, при этом Ψ(φ)=C·exp(imφ)

Постоянную C можно найти из условия нормировки пси-функции:

²dφ=1

c2·2π=1; c=

Ψ(φ)= · exp(imφ)

Квантование момента импульса.

Покажем, что момент импульса также квантуется. Мы покажем это , не решая Ур-е Шр.:

L²=L_x²+L_y²+L_z²-в классической физике

В квантовой физике в силу изотропности среды по всем направлениям можно написать, что среднее значение < L²>=3 L_z², при этом среднем значении физические величины должны отождествляться со значением , полученным в результате измерения L²=< L²>=3 L_z² , тогда L²=2Ћ²> , где m²Ћ²–квадрат проекции момента импульса на ось .

Тогда это выражение можно записать в следующем виде:

L²=2Ћ²> =(1/(2γ+1))², где

γ-максимальное значение квантового числа m, а 2γ+1- это число возможных значений квантового числа m, тогда:

²=2²=2γ(γ+1)(2γ+1)/6=(1/3)γ(γ+1)(2γ+1), тогда получаем:

L²_γ=3Ћ²γ(γ+1)(2γ+1)/3(2γ+1)=Ћ²·γ(γ+1)

L_γ= Ћ, где γ=0,1,2,3,…

γ-вращательное квантовое число.
Двухатомная молекула как квантовый жёсткий ротатор. Вращательный спектр двухатомной молекулы.

Если пренебречь изменением межъядерных расстояний, которое возникает при энергетических переходах, в качестве модели двухатомной молекулы можно принять жёсткий ротатор.

Зная, что L_γ= Ћ

L_z= mЋ

из аналогии:T=p²/2m=L²/2I

, где μ–приведённая масса двухатомной молекулы.

μd²-приведённый момент инерции двухатомной молекулы, тогда:

E= Ћ²·γ(γ+1)/2 μd², у каждой молекулы Ћ²/2 μd²=const

B= Ћ²/2 μd² (Дж)- имеет размерность энергии и называется вращательной постоянной. выражается в мЭв.

Для квантового числа существует правило отбора, т.е. ∆γ=±1 (всегда), поэтому энергетические переходы могут происходить только между соседними энергетическими уровнями.

Eγ=B·γ(γ+1)

E_γ+1,γ=E _γ+1-E _γ=B(γ+1)(γ+2)-Bγ(γ+1)=2B(γ+1), т.е. даже если на меньшем вращательном уровне получим разность 2В.

Спектр двухатомной молекулы как жёсткого ротатора.

Если есть переход с одного уровня на другой, то энергия фотона, поглощенного или испущенного двухатомной молекулой при изменении вращательной энергии выражается так:

E= Ћω_излуч.=∆ E_γ+1,γ=2B(γ+1)

ω_излуч.=(2B/Ћ)(γ+1)

Спектральные линии чисто вращательного спектра поглощения и (или) излучения какого-либо химического соединения отстают друг от друга на 2В по шкале энергий. |2B|2B|2B|2B|2B|…

Излучать или поглощать электромагнитные волны( в инфракрасной части спектра) могут только молекулы типа, т.е. молекулы с отличным от нуля дипольным моментом.

Молекулы типа Н2,дипольный момент которых равен нуля излучать или поглощать электромагнитные волны не могут, и в этих молекулах энергетических энергетически далеко происходит безысключательно. И в этом случае энергии

При переходе квантовой энергии из одного энергетического состояния(например Е₂) в другое энергетическое состояние (например Е₁) излучается всегда фотон:

E₂-E₁=Ћω_ф

Вид спектра определяется:

1)энергетическим спектром системы;

2)правилом отбора;

3)вероятностью возможных переходов.

Атом водорода по теории Бора.

1913 г. Резерфорд в Кембридже установил, что каждый атом состоит из атома и электронной оболочки.

Постулаты Бора (постулаты стационарных состояний):

В атоме существуют не изменяющиеся во времени состояния, при которых атом не излучает и не поглощает энергию, в этом состоянии электрон, двигаясь по круговой орбите, имеет дискретные квантовые значения момента импульса, удовлетворяющие условию:

mv_nr_n=nЋ, где n=1,2,3,4,…

v_n-скорость электрона на n-ой орбите

r_n-радиус n-ой орбите

Второй постулат правило частот:

при переходе электрона с одной стационарной орбиты на другую излучается один фотон:

E_n-E_m=Ћω

с энергией, равной разности энергий, соответствующих стационарным состояниям.

Набор значений ω

ω=( E_n-E_m)/π

даёт линейчатый спектр атома водорода в соответствии с теорией Бора.

Электрон в атоме водорода и водородоподобных частицах, содержащих ядро и 1 электрон(это ионы) вращается(или будет вращаться) по орбите радиуса , если центростремительная сила, удерживающая электрон на орбите будет равна кулоновской силе.

F_кул=F_центр
Ze²/4πε₀r_n²=m v²_n/ r_n (1)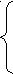
mv_nr_n=nЋ (2)
Если взять (1) и (2) и выразить неизвестные v_n и r_n:

r_n=(4πε₀Ћ²/Ze²m)·n² (3)

При z=1 и n=1 получаем r₁=a=52,2 пм

подставив (3) найдём v_n:

v_n=Ze²/4πε₀nЋ v≈10⁶ м/с

U=eφ

Потенциальная энергия заряда, находящегося в некоторой точке электрического поля равна произведения этого заряда на потенциал поля в этой точке. Поле создаётся положительного заряда и на расстоянии от ядра.

Тогда потенциал поля в точке, где есть электрон, будет равен:

φe=Ze/4πε₀r_n, тогда U=-Ze²/4πε₀r_n²

Потенциальная энергия электрона в поле ядра отрицательна, значит максимальное значение потенциальной энергии электрона будет равна нулю при r→∞

кинетическая энергия электрона на n-ой орбите:

T=mv_n²/2=(m/2)· Z²e⁴/16π²ε₀²n²Ћ²

U= - Z²e⁴/16π²ε₀²n²Ћ²

Полная энергия электрона на орбите:

E=T+U=(m/2)· Z²e⁴/16π²ε₀²n²Ћ²-Z²e⁴/16π²ε₀²n²Ћ² =- Z²e⁴m/32π²ε₀²n²Ћ²

(полная энергия отрицательна)

Знак “-” в полной энергии означает, что электрон в атоме находится в связанном состоянии. Из (*) следует, что энергетическое состояние атома водорода представляет собой последовательность уровней, изменяющихся в зависимости от квантового числа n и это целое число n, определяющее энергетический уровень называется главным квантовым числом . Энергетическое состояние электрона с n>1 называется возбужденными состояниями при n=2 наблюдаем низшее возбужденное состояние

E₁= -13,55 Эв, т.е. если мы приложим к электрону энергию 13,55 Эв, то он покинет поле ядра

E₂= -3,38Эв (это всё при Z=1)

E₃= -1,52Эв (у гелия Z=2, т.е. все энергии в 4 раза больше, у лития Z=3, т.е. все энергии в 9

E₄= -0,83Эв раз больше).

E₅= -0,54Эв

E₆= -0,38Эв

Схема энергетических переходов в атоме водорода.

E_n= - Z²e⁴m/32π²ε₀²n²Ћ²

Для водорода:

E₁= -13,6Эв

E₂= -3,38Эв
E₃= -1,5Эв

E₄= -0,84Эв

E₅= -0,53Эв

E₆= -0,38Эв

E₇≈ 0

Энергия атомов возрастает вместе со значением n (уменьшается отрицательная величина) энергетические уровни сближаются к границе, соответствующей n→∞ и атом водорода обладает минимальной энергией E₁= -13,6Эв и максимальной энергией E_∞=0 при n→∞. Это происходит(последний случай) при удалении электрона из атома, следовательно эта энергия соответствует ионизации атома. Если атому водорода, который находится в основном состоянии, сообщить энергию в +13,6Эв, то это и будет его энергии ионизации, когда электрон покинет атом. согласно второму постулату Бора пи переходе электрона с одной стационарной орбиты на другую излучается или поглощается 1 фотон, т.е. получаем:

Ћω= E_n2-E_n1= [Z²e⁴m/32π²ε₀²n²Ћ²](1/n₁²-1/n₂²)

2πЋc/λ= [Z²e⁴m/64π³ε₀²n²Ћ³c](1/n₁²-1/n₂²)

R=1,1·10⁷ 1/м –постоянная ридберга

1/λ=Z²R(1/n₁²-1/n₂²)-сериальная формула

Если атом возбуждается полностью, т.е. электрон ушёл и осталось ядро, у нас возбуждается полный спектр.

Кроме Лаймана все волны в инфракрасном спектре.

Согласно второму постулату Бора атом излучает свет при переходе электрона с одной орбиты на другую, расположенную ближе к ядру. Все линии спектра, получающиеся при переходе электрона на первую орбиту( со 2,3 и т.д.) представляют собой линии одной серии, отвечающие значению n1=1 и все эти линии принадлежат УФ части спектра.

При переходе на орбиту с n=2( с 3,4,5, и т.д. орбит) получаются линии серии Бальмера и это видимый свет во всём оптическом диапазоне.

Линии, приходящиеся на третий уровень( с 4,5,6 и т.д.) лежат в инфракрасной части спектра электромагнитных волн.

Спектр поглощения также является линей чатым, но он содержит всегда только серию Лаймана. Так как свободные атомы водорода обычно находятся в основном состоянии (n=1), то при сообщении этим атомам энергии извне могут наблюдаться только переходы из основного состояния в возбужденное и поэтому появляется только серия Лаймана.

Теория Бора позволила точно определить спектр атома водорода.

Теория Бора обладает внутренним противоречием, т.к. в ней использованы с одной стороны все законы классической физики, а с другой стороны начальные элементы квантовой физики, поэтому эта теория не могла ответить на вопрос: откуда берутся переходы и не смогла описать спектр атома гелия, т.е. простейшего атома, следующего сразу за водородом в таблице Менделеева.