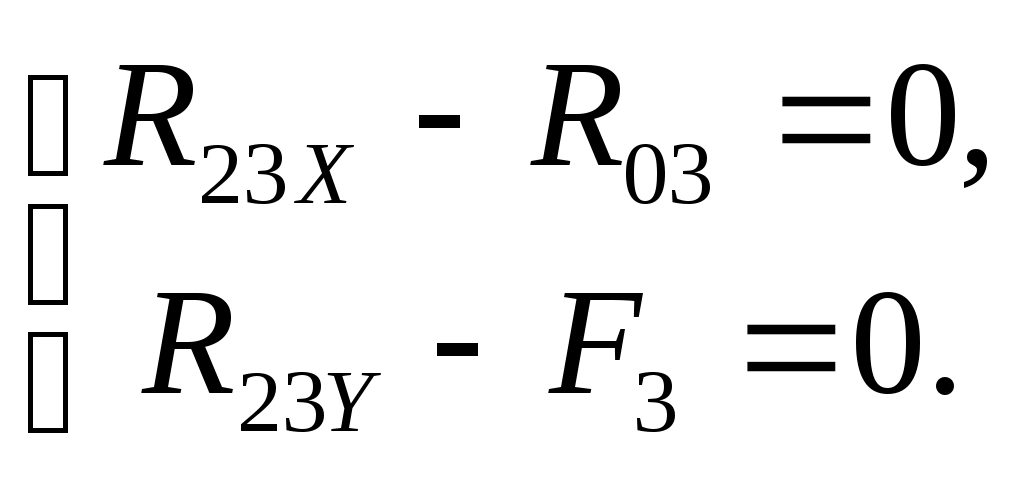3.2. Силовой расчёт группы Ассура второго класса.
Для выполнения силового расчёта необходимо знать значение сил, действу- ющих на звенья механизма: силы тяжести, движущие силы и силы инерции этих звеньев.
Силовой расчёт будем вести для десятого положения кривошипно-ползунного механизма.
От механизма, начиная с исполнительного звена ползуна, отсоединяется группа Ассура, а точки разрыва этой группы заменяются реакциями.
3.2.1.Определение сил инерции.
Модули сил инерции звеньев определяем по формуле:
Фimiai , (0)
где mi-масса i-го звена, кг
ai-ускорение центра масс i-го звена, мс2 .
Подставив числовые значения, получим:
Ф2100·599599Н
Ф3200494988Н
Направления сил инерции противоположны направлениям соответствующих ускорений. Момент инерции шатуна определяется по формуле:
MФ2IS22 (0)
MФ22,0319,1938,96Нм
Систему сил инерции шатуна, т.е. главный вектор сил инерции Ф2, приложенный в центре масс, и момент сил инерции относительно центра масс, приводим к одной силе Ф2 приложенной в некоторой точке K. Расстояние между линиями действия силы инерции и приведенной силой вычисляется по формуле:
hMФ2Ф2 (0)
h38,965990,065 м
Направление приведенной силы совпадает с направлением силы инерции, а направление момента приведенной силы относительно точки S2 совпадает с направлением момента MФ2 Рисунок 2.
3.2.2.Определение сил тяжести.
Силы тяжести определяем по формуле:
Gimig , (0)
где miмасса i-го звена, gускорение силы тяжести.
Подставив числовые значения, получим:
G21009,81981Н
G32009,811962Н.
3.2.3. Определение реакций в кинематических парах.
Определение давлений в кинематических парах начинаем с рассмотрения равновесия группы Ассура 2-3 Рисунок 3: шатун AB – ползун B. На звенья этой группы действуют силы: движущая сила Fд, силы тяжести G3, G2, результирующие силы инерции Ф3, Ф2, реакция R03 заменяющая действие стойки 0 на ползун 3 и реакция R12 заменяющая действие кривошипа 1 на шатун 2.
Силы, приложенные в точке B, приводим к одной силе F3.Величину этой силы определяем по формуле:
F3Fпс+Фu (0)
F3988Н
Знак показывает, что сила F3 направлена вверх.
Условие равновесия группы 2-3 выражается следующим образом:
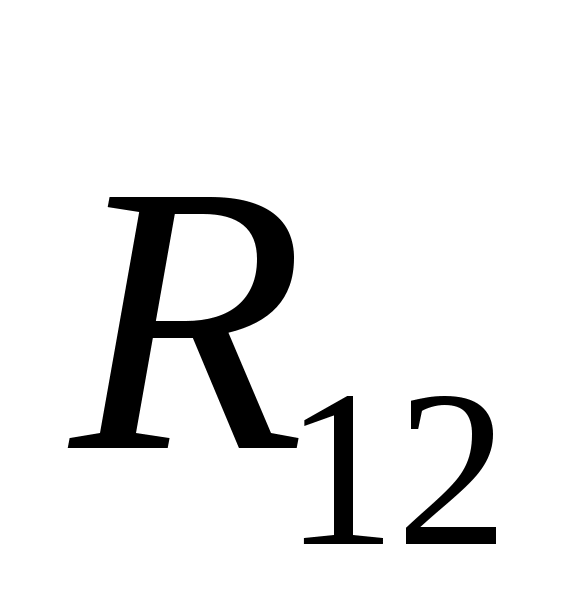 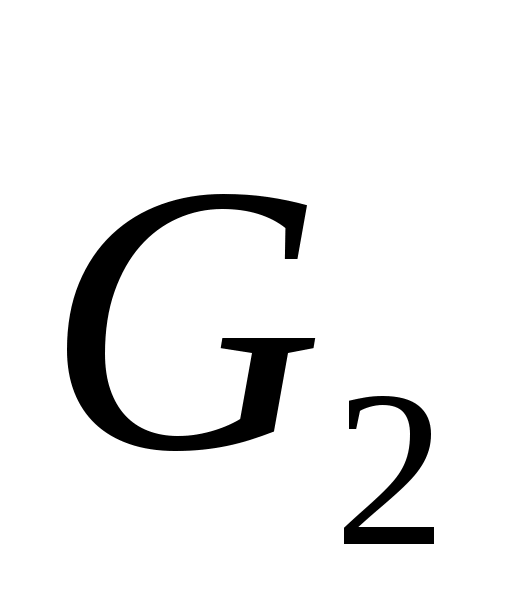 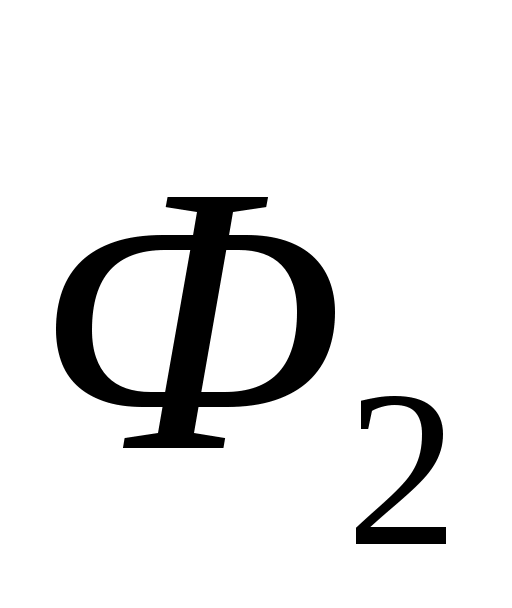 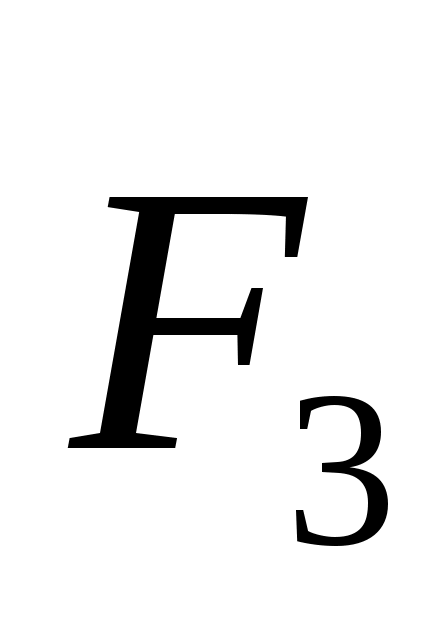 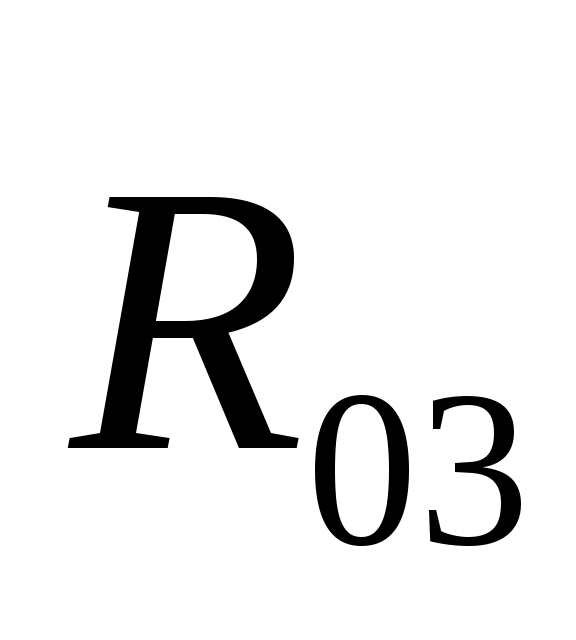 0 (0) 0 (0)
Давление R12 раскладываем на две составляющие, действующие вдоль оси звена AB – R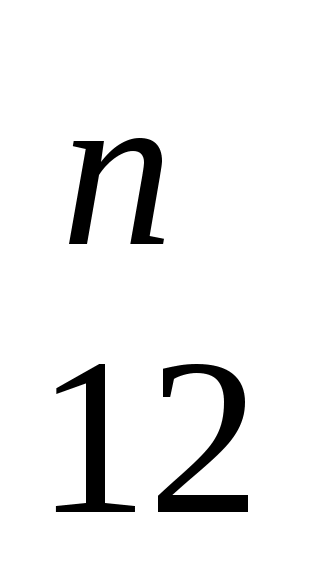 и перпендикулярно к оси звена AB – R и перпендикулярно к оси звена AB – R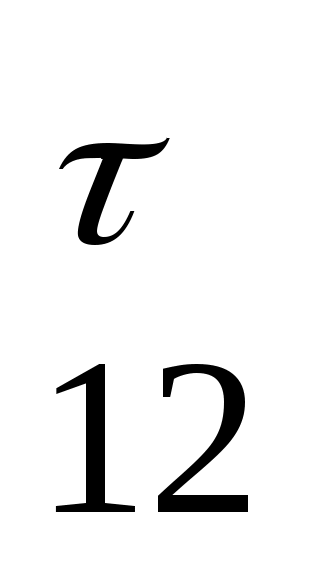 . .
Составляющую R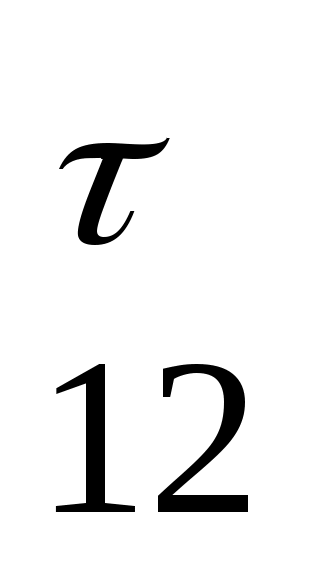 определяем из уравнения моментов всех сил, действующих на шатун AB, относительно точки B. определяем из уравнения моментов всех сил, действующих на шатун AB, относительно точки B.
Применительно к рисунку 3 это уравнение можно записать так:
-R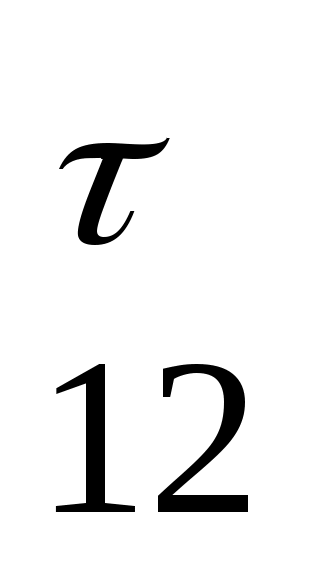 ABФph1G2h20 (0) ABФph1G2h20 (0)
откуда
R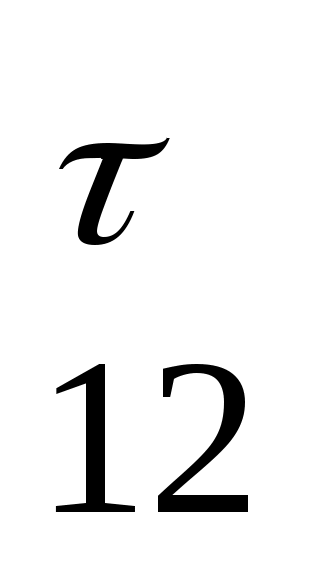 Фph1G2h2AB (0) Фph1G2h2AB (0)
R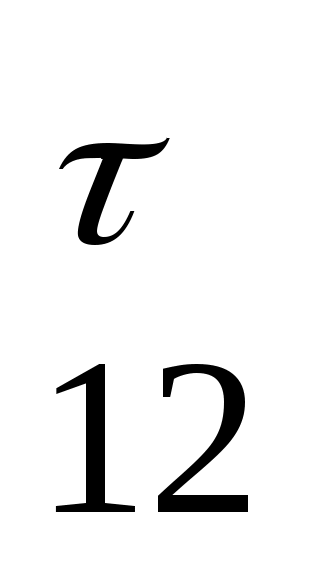 59910,698114,623,1345 Н. 59910,698114,623,1345 Н.
План сил строим в масштабе: F=13 Нмм.
Из произвольной точки последовательно откладываем вектора R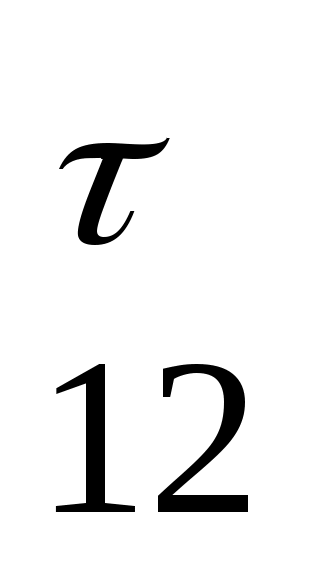 , F3G2,Ф2. Через конечную точку вектора Ф2 проводим линию действия реакции R03 ,а через начальную точку вектора R , F3G2,Ф2. Через конечную точку вектора Ф2 проводим линию действия реакции R03 ,а через начальную точку вектора R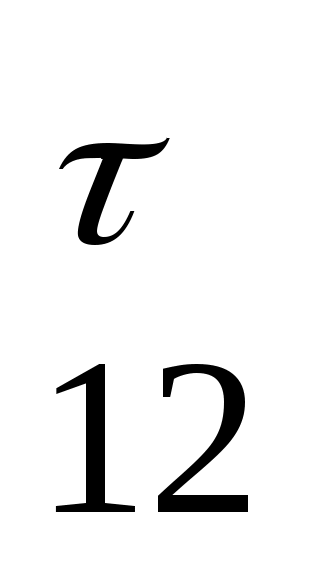 линию действия силы R линию действия силы R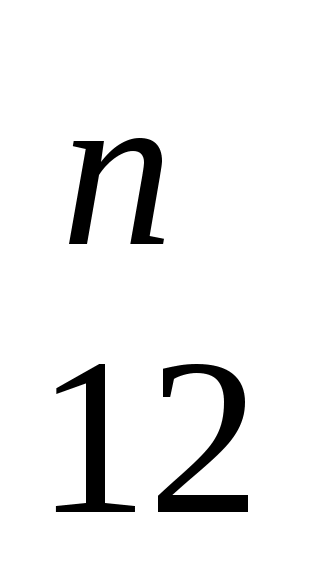 . Получим точку пересечения. Соединив конечную точку вектора Ф2 с точкой пересечения, получим вектор R03. Соединив точку пересечения с конечной точкой вектора R . Получим точку пересечения. Соединив конечную точку вектора Ф2 с точкой пересечения, получим вектор R03. Соединив точку пересечения с конечной точкой вектора R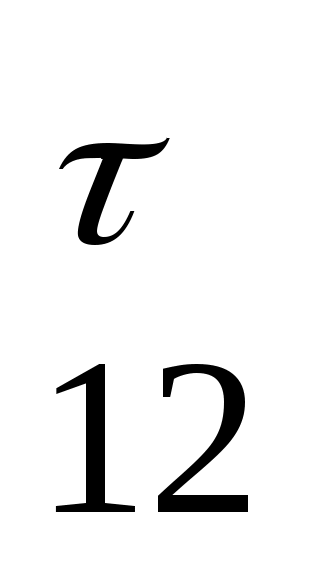 , получим вектор R12.Умножив соответствующие длины на масштабный коэффициент, получим R032639 H R121443 H R , получим вектор R12.Умножив соответствующие длины на масштабный коэффициент, получим R032639 H R121443 H R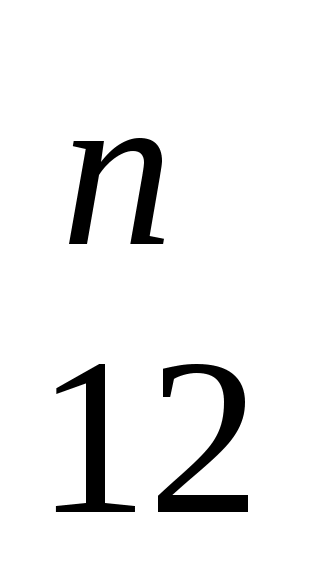 345 Н 345 Н
Если из произвольной точки отложить вектор R12 для всех двенадцати положений, то получим годограф реакции R12.
По результатам расчета программы ТММ1 строим годограф реакции R12 в масштабе R=221,3 Нмм.
Если в каждом из двенадцати положений ползуна отложить вектор R03 и соединить их конечные точки плавной кривой, то получим годограф реакции R03.
По результатам расчета программы ТММ1 строим годограф реакции R03R03SB в масштабе R114,68Нмм.
Давление R32 в паре шатун – ползун определяем из условия равновесия ползуна:
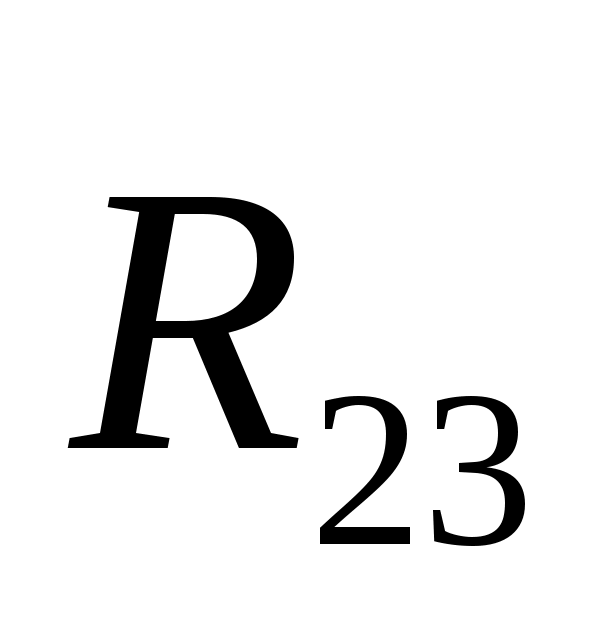 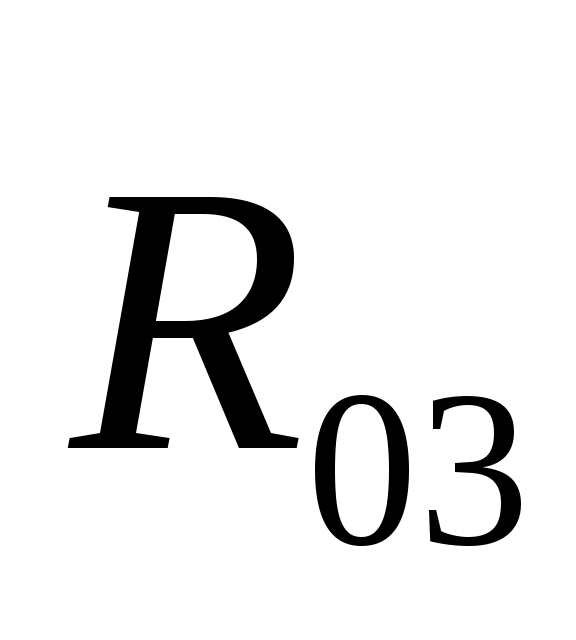 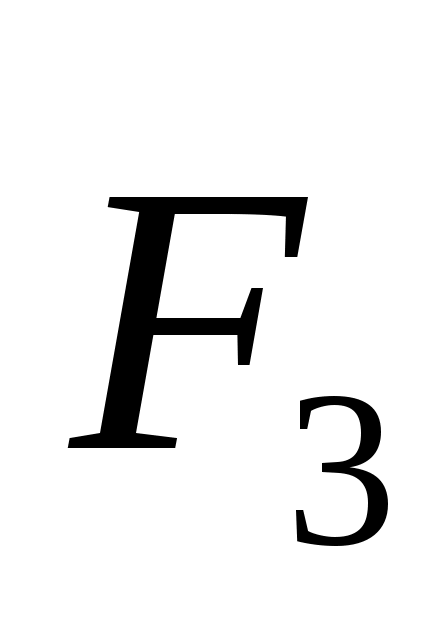 0 (0) 0 (0)
и равенства:
R32R23, (0)
или
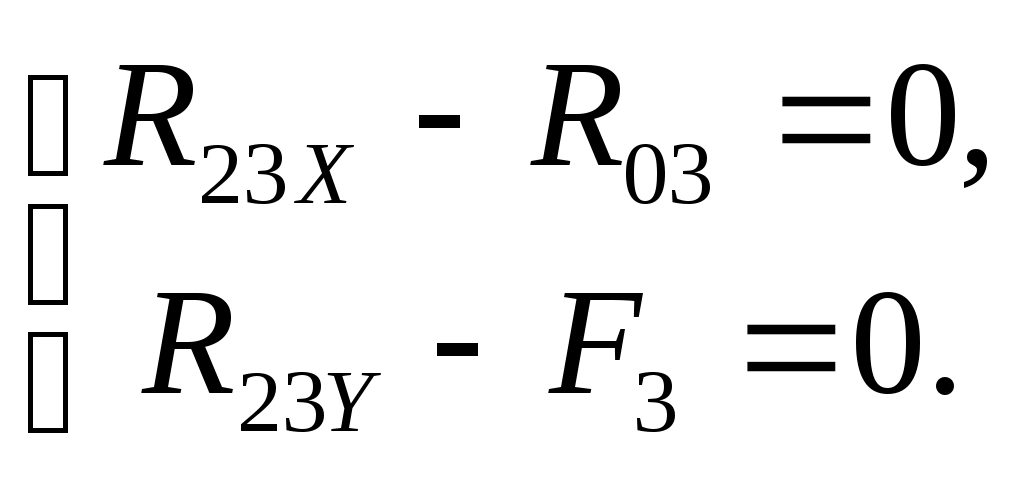 (0) (0)
Тогда
R23XR03_H,
R23YF3_ H
R23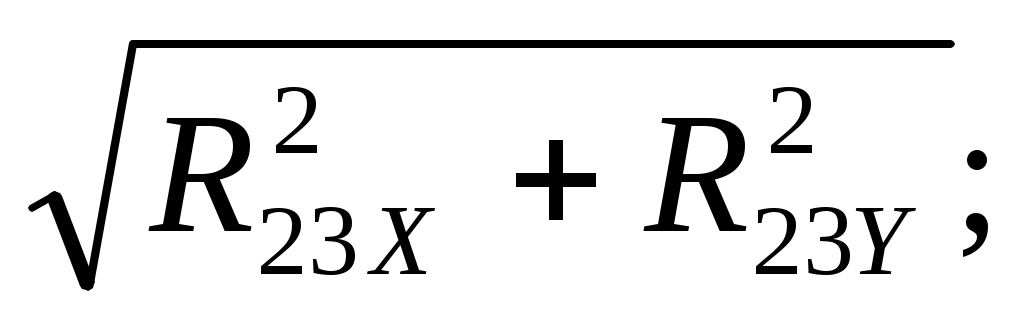 (0) (0)
По результатам расчета программы ТММ1 строим диаграмму реакции R32R321 в масштабе: R=261,72 Нмм.
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.