Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb.
|
3.10. Как ставить запятую при приближённом умножении и деленииКогда нужно определить место запятой при умножении и делении точных десятичных чисел, мы пользуемся определёнными правилами. Такого же рода правила существуют и для приближённых действий, но они громоздки и на практике ими не пользуются. Во всех разобранных нами примерах мы ставили запятую «по соображению». Дадим теперь общие указания, которые помогут рационализировать эти «соображения». Рассуждение сводится к тому, что оба сомножителя (в случае умножения) или делимое и делитель (в случае деления) округляются (в уме) так, чтобы в каждом из них осталась одна верная цифра. Если эта цифра велика (7, 8 пли 9), то заменяем её единицей высшего разряда. Полученные однозначные числа легко разделить или перемножить. Получается очень грубый приближённый результат, который всё же позволит судить, где в окончательном итоге должна быть запятая. Рассмотрим примеры: 1) 17,3∗27,9. Первый множитель близок к 20, второй - к 30. Значит, произведение должно быть близко к 600 (20∗30 = 600), т.е. в нём будет три цифры левее запятой. 2) 0,891∗0,0235. Первый множитель близок к 1, второй к 0,02. Значит, произведение будет близко к двум сотым, т.е. будет иметь один нуль после запятой. 3) 34,2:8210. Делимое близко к 30, делитель к 10000. Деля 30 на 10000, получим: 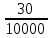 = 0,003. Значит, в частном должно быть два нуля после запятой.4) 76,3:0,000317. Делимое близко к 100, делитель к 0,0003. Деля 100 на 0,0003, получим 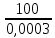 =  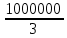≈ 300000. Значит, в частном до запятой должно быть шесть цифр.3.11. О приближённом извлечении квадратных корнейМы знаем, что произведение некоторого числа на равное ему число (произведение двух одинаковых сомножителей) называется второй степенью или квадратом данного числа. Часто приходится решать обратную задачу: по данному квадрату находить число. Узнаем, например, длину комнаты, если известно, что длина и ширина её одинаковы, а площадь равна 36 квадратным метрам. В этой задаче требуется найти число, которое при умножении само на себя даёт 36. Такое число нетрудно найти подбором: это будет 6. Значит, длина и ширина комнаты должны быть по 6 метров. Если бы по-прежнему было известно, что длина и ширина комнаты одинаковы, но площадь её была бы 29 квадратных метров, то решить задачу мы не сумели бы. Ясно, что длина комнаты больше 5 м (5∗5=25) и меньше 6 м (6∗6=36), значит, это будет 5 с какой-то дробью. Но с какой именно? Чтобы отвечать на такие вопросы, нужно познакомиться с новым арифметическим действием - с извлечением квадратного корня. Квадратным корнем из данного числа называется такое число, которое при умножении само на себя даёт данное число. Например, квадратным корнем из девяти будет три, потому что трижды три - девять. Точно так же квадратным корнем из 25 будет 5, квадратным корнем из 100 будет 10, квадратным корнем из 1 будет 1. Для квадратного корня употребляется значок 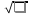 , который называется радикалом. 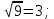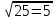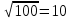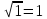Пишут:  ;  ;  .Действие, с помощью которого по данному числу находят его квадратный корень, называется извлечением квадратного корня. При извлечении квадратных корней следует помнить наизусть таблицу квадратов, которая является, впрочем, частью обыкновенной таблицы умножения. Вот эта таблица:
Заметим, что нацело корень извлекается очень редко. Почти всегда корень извлекают приближённо, с той или иной степенью точности. Мы рассмотрим только приближённое извлечение корней с тремя верными цифрами. В том числе, из которого извлекаем корень (его называют подкоренным числом), тоже будем сохранять три верные цифры. |