Берман. Государственное издательство техникотеоретической литературы

• Название: Государственное издательство техникотеоретической литературы
• Анкор: Берман
• Дата: 11.02.2021
• Размер: 233.41 Kb.
• Имя файла: Berman_Priemy-bystrogo-scheta-2-e-izdanie-.328005 (1).docx
• Тип: Документы; #175545
• страница: 14 из 22

ГЛАВА III

ПРИБЛИЖЁННЫЕ ВЫЧИСЛЕНИЯ

3.1. Точные и приближённые значения величин

При счёте каких-нибудь предметов обычно нам удаётся точно узнать их число. Если я говорю, что у меня на руке пять пальцев, или что рабочий изготовил 320 втулок, то числа 5 и 320 точно выражают количество сосчитанных предметов. Иначе обстоит дело, когда мы говорим, что в 1939 году в городе Рыбинске было 55500 жителей. Ведь жители рождаются и умирают, приезжают и уезжают; число их всё время меняется. Да если бы оно и не менялось, всё равно подсчитать всех до единого жителей города очень трудно: одних можно случайно пропустить, других сосчитать дважды. Ошибка при счёте на 2-3 десятка вполне возможна. Значит, когда мы говорим, что в Рыбинске было 55500 жителей, мы имеем в виду, что их было около 55500; может быть 55550, может быть 55472, может быть ещё какое-нибудь число, близкое к 55500. В этом случае 55500 даст нам приближённое число жителей города.

Всё же, счёт, как правило, даёт точные значения чисел и лишь в редких случаях - приближённые. Иначе обстоит дело при измерении или взвешивании различных предметов. Если нам отвесили 800 г хлеба, то это вовсе не значит, что наш хлеб весит ровно 800 г. Ведь торговые весы - инструмент грубый; если мы, уравновесив на чашках 800 г, добавим на одну из чашек 5 г (это - очень маленькая гирька; её придётся взять из аптекарского разновеса; в продуктовых магазинах таких мелких гирь, обычно, не бывает), то равновесие не нарушится. Значит, наш хлеб может весить и 805 и 810 г, а может и 793 или 798 г. Число 800 г выражает его вес приближённо.

Очень поучителен следующий опыт. Несколько человек измеряют один и тот же предмет, например, ширину стола. При этом почти наверное у всех получатся несколько отличающихся одно от другого числа. Один получит, например, 883 мм, другой 885 мм, третий 881 мм и т.д. Приняв ширину стола в 883 мм, мы получим, как и в предыдущем примере, приближённое значение этой ширины.

Все без исключения измерения приводят к приближённым значениям измеряемых величин. Но в некоторых случаях измерения проводятся очень грубо - тогда получаются большие ошибки. В других случаях приходится делать тщательные измерения; тогда и ошибка получается малая. Полная точность при измерениях не достигается никогда.

Раз мы сознаём, что все наши измерения несовершенны, то естественно возникают такие вопросы: как охарактеризовать качеству измерения, степень его точности? Как производить арифметические действия с числами, выражающими интересующие нас величины только приближённо? Не будет ли увеличиваться ошибка, если мы над приближённой величиной будем совершать арифметические действия? Нельзя ли, пользуясь тем, что сами данные приблизительны и ответ нас интересует приближённый, упростить арифметические действия?

Особенно важен последний вопрос - вопрос об упрощении арифметических действий при работе с приближёнными значениями измеряемых величин. К нему можно подойти с другой стороны. Когда изготовляется по стандарту или по чертежу какой-нибудь предмет, то допускается известное отклонение от указанных на чертеже размеров, иногда - довольно значительное, иногда - весьма малое. Например, для круглого железа обычной прокатки диаметром в 20 мм допускаются уклонения на мм в ту и другую сторону. В случае очень точной прокатки отклонение допускается только в 0,3 мм. Если изготовление предмета по чертежу связано с предварительным расчётом (например, нужно подсчитать, какой подобрать резец и т. п. ), а результат можно получить приближённый, то можно ожидать, что и сами вычисления можно выполнять как-то упрощённо, нужно следить за тем, чтобы ошибка при вычислениях не превзошла указанного допуска.

На все вопросы такого рода отвечает особый отдел математики, который называется учением о приближённых вычислениях. Наша задача познакомиться с началами этого учения.

3.2. Абсолютная и процентная погрешность

Допустим, что ширина стола 784 мм, а мы, измерив её, получили 781 мм. Разница между точным значением измеряемой величины и её приближённым значением называется абсолютной погрешностью. Мы скажем, что найденное нами приближённое значение измеряемой величины имеет абсолютную погрешность 3 мм. На практике мы никогда не знаем точного значения измеряемой величины, поэтому не можем точно знать абсолютную погрешность. Но обычно мы знаем точность приборов, с которыми мы работаем, учитываем ловкость или нелоькость лица, производящего измерения и т.д. Всё это даёт возможность составить известное суждение об абсолютной погрешности измерения.

Если, например, мы обычной линейкой или рулеткой измеряем длину комнаты, то нам нетрудно будет учесть метры и сантиметры, но вряд ли мы сможем учесть миллиметры. Да в этом и надобности нет. Поэтому мы сознательно допускаем ошибку в пределах одного сантиметра. Абсолютной погрешностью нашего приближённого значения длины комнаты будет 1 см. Точно так же при взвешивании на торговых весах грузов, близких к килограмму, вполне возможно ошибиться грамм на 10. Купив, например, 800 г хлеба, мы можем сказать, что 800 г - это приближённый вес нашего хлеба с абсолютной погрешностью в 10 г³.

Абсолютная погрешность не является показателем того, хорошо или плохо произведено измерение. Если известно, что, измерив некоторую длину, мы получили абсолютную погрешность в 1 см, то никаких заключений о том, хорошо или плохо мы мерили, сделать нельзя. Если мы измеряли длину карандаша в 15 см и ошиблись на один сантиметр, то наше измерение никуда не годится. Если же мы измеряли двадцатиметровый коридор и ошиблись всего на 1 см, то наше измерение - образец точности. Важна не сама абсолютная погрешность, а та доля, которую она составляет от измеряемой величины. 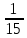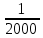В первом примере абсолютная погрешность (1 см) составляет долю измеряемой величины (15 см), во втором (20 м составляют 2000 см).

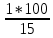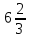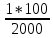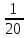Обычно эти доли выражают в процентах. В первом примере абсолютная погрешность составляет = % измеряемой величины; во втором – = %. Сразу видно, что второе измерение значительно лучше первого.

Выраженная в процентах доля, которую абсолютная погрешность составляет от всей измеряемой величины, называется процентной погрешностью. Качество всякого измерения характеризуется процентной погрешностью приближённого результата.

Легко дать правило для определения процентной погрешности. Нужно абсолютную погрешность умножить на 100 и разделить на саму измеряемую величину (или на её приближённое значение⁴.

Примеры: При измерении длины в 5 м допущена абсолютная погрешность в 25 см. Найти процентную погрешность.

Ищем, какой процент 25 см составляют от 500 см (5 м - 500 см). Получаем 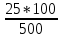= 5%.

Это и будет процентная погрешность.
При взвешивании 800 г допущена неточность в 10 а. Найти процентную погрешность.
При подсчёте числа жителей города, которое оказалось равным 55000, допущена погрешность в 40 человек. Найти процентную погрешность.
При прокате круглого железа диаметром в 30 мм допускается неточность в 3% (процентная погрешность). На сколько миллиметров можно ошибиться при прокате этого железа, не делая брака?
Отв. 0,9 мм.