Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb. Скачать 233.41 Kb.
|
2.7. Деление многозначных чиселПри делении полезно обратить внимание на два случая: 1) делимое раскладывается на слагаемые, каждое из которых легко делится на делитель, и 2) делитель разлагается на множители. Рассмотрим эти случаи. Разделим 385 на 35. Имеем 385=350+35. Значит, 385:35=(350+35):35. Триста пятьдесят при делении на 35 даст 10, а тридцать пять при делении само на себя даёт единицу. Всего получаем 11. Значит, 385:35=11. Ещё пример: разделим 2837 на 14. Имеем 2837=2800+28+9. Делим каждое из слагаемых на 14; получаем 200, 2 и 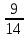 . Все полученные числа складываем: получим 202 . Все полученные числа складываем: получим 202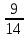 . Записывается действие так: . Записывается действие так:2837:14=(2800+28+9):14=200+2+ 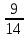 =202 =202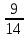 . .Если делим число, близкое к «круглому», легко делящемуся на делитель, то записываем делимое в виде разности двух чисел: «круглого числа» и дополнения. Дальше поступаем, как в предыдущем случае, только результаты не складываем, а вычитаем. Разделим, например, 3104 на 32. Имеем 3104=3200-96. Делим 3200 на 32, получаем 100; делим 96 на 32, получаем 3. Вычитая 3 из 100, получим окончательный ответ: 97. Записываем всё это так: 3104:32=(3200-96):32=100-3=97. Перейдём ко второму случаю. Разделим 4698 на 54. Делитель легко представить как произведение однозначных чисел: 54=6х9. Делить на однозначные числа легко. Поэтому делим наше число на 6, а потом то, что получится, разделим на 9. Располагаем действие так: 4698:54=? 4698:6=783; 783:9=87. Получается значительно проще, чем по обычному правилу деления. Этим мы ограничимся. В остальных случаях вернее и удобнее применять обычное правило деления. Примеры: 3468:17; 1776:48; 8557:43; 15195:15; 2048:32; 3969:63; 2296:56; 16665:15; 10240:64; 10149:51. 2.8. Вычисления с простыми и десятичными дробямиПри решении практических задач часто приходится иметь дело одновременно и с простыми, и с десятичными дробями. Приходится, например, выполнять действия, вроде следующих: 0,3 + 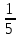 ; ; 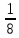 - 0,017; - 0,017;  ∗0,13; ∗0,13;  :4,6 и т.д. Заметим, что при сложении и вычитании нужно либо все дроби превратить в простые, либо все в десятичные. Удобнее считать, пользуясь десятичными дробями. Поэтому обычно все дроби переводят в десятичные. Особенно удобно это в том случае, если ищется приближённый результат. Если же знаменатели дробей невелики и требуется точный результат, то лучше превращать все десятичные дроби в простые, чтобы не иметь дела с периодическими дробями. :4,6 и т.д. Заметим, что при сложении и вычитании нужно либо все дроби превратить в простые, либо все в десятичные. Удобнее считать, пользуясь десятичными дробями. Поэтому обычно все дроби переводят в десятичные. Особенно удобно это в том случае, если ищется приближённый результат. Если же знаменатели дробей невелики и требуется точный результат, то лучше превращать все десятичные дроби в простые, чтобы не иметь дела с периодическими дробями.Напомним, как обратить десятичную дробь в простую: превратим, например, 0,36 в простую дробь. Прочитываем эту дробь; имеем тридцать шесть сотых; значит, знаменателем будет 100, а числителем 36. Записываем  и сокращаем насколько можно; в нашем примере можно сократить на 4. Получаем и сокращаем насколько можно; в нашем примере можно сократить на 4. Получаем0,36 =  = = 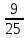 . .Итак, чтобы превратить десятичную дробь в простую, прочитываем десятичную дробь и записываем её в форме простой дроби так, как читаем; затем, что можно - сокращаем. Если нужно превратить простую дробь с десятичную, то делим числитель на знаменатель по обычным правилам. Чаще всего деление продолжается при этом без конца (получается периодическая дробь) и приходится довольствоваться приближённым результатом. Примеры: 1) Превратить 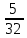 в десятичную дробь. Делим 5 на 32. в десятичную дробь. Делим 5 на 32.
Получим 0, 15625. 2) Превратить 3/7 в десятичную дробь. Делим 3 на 7:
Деление никогда не закончится. Получится периодическая дробь 0,428571428571428571..., которую записывают часто так: 0,(428571), т.е. пишут только первый период, но заключают его в скобки. Примеры: превратить в простые дроби: 0,72; 0,0128; 0,625; 0,17; 0,3; 0,2. Превратить в десятичные дроби:  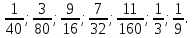 Если нужно сложить или вычесть дроби, среди которых есть и простые с небольшими знаменателями, и десятичные, то превращаем все дроби в простые и выполняем действие по обычным правилам. Примеры: 1) 0,42 + 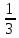 + + 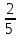 + 0,016 = + 0,016 == 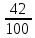 + + 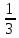 + + 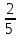 + +  = ==  + + 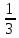 + + 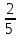 + +  = == 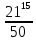 + +  + +  + + 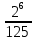 = ==  = =  = 1 = 1 . .Общий знаменатель 750. Дополнительные множители 15, 250, 150 и 6. 2) 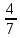 - 0,48 = - 0,48 = 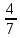 - -  = =  - - 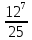 = = 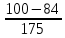 = =  3) 0,096 -  = =  - -  = =  - -  = = 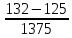 = =  . .При умножении и делении нет надобности сводить все данные дроби либо только к простым, либо только к десятичным. Действуем с десятичными дробями по тем же правилам, как и с целыми числами. Умножим, например, 4,5 на  . Пишем: . Пишем:4,5∗  = =  = = 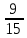 = =  . .Нет никакой надобности превращать 4,5 в простую дробь или в десятичную. Разделим, далее, 0,133 на  . Пишем: . Пишем: = =  = =  = 0,19∗5 = 0,95 = 0,19∗5 = 0,95Всё выполняется просто и гладко. Заметим, что помнить все правила деления дроби на целое число, целого числа на дробь и т.д. не нужно. Важно твёрдо помнить правило деления дроби на дробь: числитель первой дроби умножается на знаменатель второй, это будет числитель частного; знаменатель первой дроби умножается на числитель второй, это будет знаменатель частного. Ещё лучше просто представлять себе схему (деление дробей «крест-накрест»). 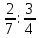 = = 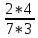 = = 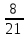 Если делимое (или делитель) будет целым числом (или десятичной дробью), то подписываем под ним в качестве энаменателя единицу (от этого число, разумеется, не меняется) и пользуемся правилом деления дроби на дробь. Примеры на умножение: 0,24∗ 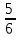 ; 0,72∗ ; 0,72∗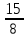 ; ;  ∗0,056; ∗0,056; 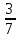 ∗0,18; 0,311∗ ∗0,18; 0,311∗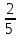 ; 0,14∗ ; 0,14∗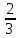 ; ; 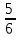 ∗0,11. ∗0,11.В последних четырёх примерах действие идёт не так гладко, как в первых трёх. Умножим, например, 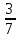 на 0,18; получим на 0,18; получим 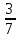 ∗0,18 = ∗0,18 =  . Сократить ничего нельзя, делить десятичную дробь на 7 - это обрекать себя на бесконечное деление. Поэтому умножаем числитель и знаменатель на 100 - чтоб устранить десятичную дробь в числителе - и получаем - . Сократить ничего нельзя, делить десятичную дробь на 7 - это обрекать себя на бесконечное деление. Поэтому умножаем числитель и знаменатель на 100 - чтоб устранить десятичную дробь в числителе - и получаем -  , а по сокращении на 2 - окончательный ответ: , а по сокращении на 2 - окончательный ответ:  . .Примеры на деление: 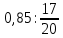 ; ; 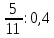 ; ; 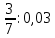 ; ; 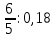 ; ; ; ;  ; ; 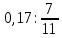 ; ; 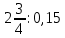 . .В последнем примере сначала превратить целое число с дробью, т.е.  , в неправильную дробь. Два даст , в неправильную дробь. Два даст 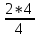 , всего восемь четвёртых, да 3 четвёртых - одиннадцать четвёртых.) , всего восемь четвёртых, да 3 четвёртых - одиннадцать четвёртых.)Если нужно перемножить несколько дробей, то сначала выписываем над чертою все числители, а под чертою - все знаменатели. Затем всё, что можно, сокращаем. И только после этого перемножаем числа, стоящие над чертою (это будет числитель), и числа, стоящие под чертою (знаменатель). Вычислим, например,  . .Записываем так:  = =  = =(сокращаем 8 и 4; 0,25 и 5; 0,034 и 17) =  = 0,9∗0,002=0,0018. = 0,9∗0,002=0,0018.Вот ещё пример: перемножим 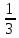 , ,  , ,  , 0,121, , 0,121, 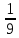 и 0,15. и 0,15.Пишем: 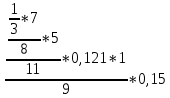 = =  = =(сокращаем 0,121 и 11; 0,15 и 3) =  = = 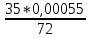 = =  = =  = = 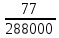 . .Примеры: 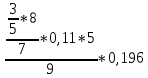 ; ;  ; ; ; ;  . .В последнем примере превратить сначала целое число с дробью в неправильную дробь. |
