Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb. Скачать 233.41 Kb.
|
2.9. Процентные вычисленияВ первой главе мы рассмотрели три основные задачи на проценты. Если данные нам числа не так просты, как это было в примерах первой главы, то задачу приходится решать на бумаге. В задачах первого типа даётся число и указывается, сколько процентов от него составляет искомая величина. Найдём, например, 23% от 845. Пишем так: 23% от 845; 23 = 20+3 20% от 845; 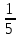 часть от 845; 845:5=169 часть от 845; 845:5=1691% от 845 = 8,45; 8,45∗3= 25,35 23% от 845 = 169+25,35 = 194,35 Иногда удобнее представлять проценты не в виде суммы, а в виде разности. Найдём, например, 45% от 264. 45% от 264; 45 = 50-5. 50% от 264 = 132 5% от 264 = 13,2 45% от 264 = 132-13,2 = 118,8 В задачах второго типа даются два числа. Требуется узнать, какой процент составляет одно от другого. Узнаем, например, какой процент от 275 составляет 15? Рассуждаем так: 275 составляет 100%, следовательно, 1 » 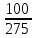 % % (единица в 275 раз меньше, чем 275), а 15 составляет 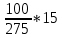 (в 15 раз больше). (в 15 раз больше).Остаётся вычислить 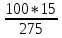 . Записываем: . Записываем:275 = 100% 1 = 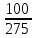 % %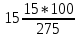 % %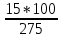 = = 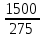 = = 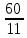 = = 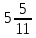 %. %.(При переходе от второй дроби к третьей мы сократили на 25.) В задачах третьего типа данное число составляет некоторый процент от искомого. Решим, например, такую задачу: 72% от некоторого числа составляют 15. Найти само это число. Рассуждаем так же, как в предыдущей задаче. 72% = 15 1% = 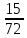 (в 72 раза меньше, чем 72%), (в 72 раза меньше, чем 72%),100% = 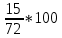 (в 100 раз больше, чем 1%). (в 100 раз больше, чем 1%).Остаётся вычислить 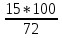 = = 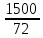 = = 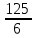 = = 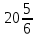 Искомое число: 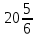 Рассмотрим задачи на проценты, которые внешне несколько отличаются от трёх основных. Задача 1-я. Сберегательная касса платит по срочным вкладам 5%. Я положил некоторую сумму денег и через год получил 1785 рублей. Какая сумма была положена? Необычность задачи в том, что даётся не сама величина, и не её доля, составляющая данный процент, а сумма самой величины и её доли. Тем не менее простое рассуждение покажет, что перед нами - обычная задача третьего типа. В самом деле, имелась некоторая сумма, составлявшая 100%, да к ней прибавилось 5%. Значит, новая сумма составляет 100+5 = 105%. Дальнейшее просто: 105% = 1785 руб. 1% = 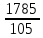 руб. (в 105 раз меньше, чем 105%). руб. (в 105 раз меньше, чем 105%).100% = 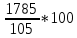 (в 100 раз больше, чем 1%). (в 100 раз больше, чем 1%).Остаётся вычислить 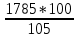 , что даёт 1700 руб. , что даёт 1700 руб.Задача 2-я. Забраковав 4% продукции, браковщик принял 2592 детали. Сколько всего было изготовлено деталей? Рассуждение такое же, как в предыдущей задаче. Из всей продукции, составляющей 100%, забраковано 4%. Значит, осталось 100-4 = 96%. Дальнейшее просто: 96% = 2592; 1% = 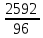 ; ;100% = 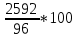 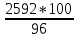 = = 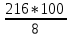 = 27∗100 = 2700 деталей. = 27∗100 = 2700 деталей.(сначала сократили дроби на 12). Задача 3-я. Население города было 44000, стало 48000 человек. На сколько процентов возросло население? Прежде всего находим прирост населения. Он равен 48000-44000 = 4000. Теперь задача свелась ко второму типу: какой процент составляет 4000 от 44000 (от первоначального числа жителей). 44000 = 100% 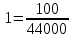 % %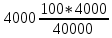 % %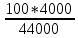 = = 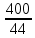 = = 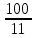 = = 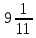 %. %.Значит, и население города увеличилось на 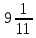 %. %.Задача 4-я. Стахановец, выполнив норму на 420%, обработал 4620 деталей. Сколько деталей обработал он сверх нормы? Несмотря на необычность постановки вопроса, это -обычная задача третьего типа. Только «доля» здесь значительно больше самого числа; но это не влияет на ход рассуждения. Рассуждаем так: 420% = 4620 деталей 1% = 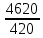 деталей деталей100% = 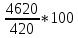 деталей деталей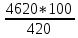 = 1100 деталей. = 1100 деталей.Значит норма - 1100 деталей, а сверх нормы 3520 деталей. Задача 5-я. Я хочу купить бумаги на 100 рублей. Один лист бумаги стоит 80 копеек, и я могу покупать со скидкой в 20%. Сколько листов я могу купить? Рассуждаем так. Узнаем сначала, сколько мне будет стоить один лист. Я уплачу за него не 80 копеек, а только 80% от этого числа (100-20 = 80), то есть 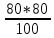 = 64 копейки = 64 копейки(задача первого типа). Значит, на 100 рублей(=10000 копеек) я могу купить 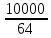 = = 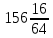 = = 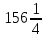 листов листовили, так как части листов не продаются, я могу купить 156 листов, и у меня ещё останется 16 копеек (стоимость 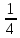 листа). листа).Продавец будет считать немного иначе. Если я попрошу его отпустить мне 156 листов, то он будет считать так: 1 лист стоит 80 копеек, 156 листов стоят 80∗16 = 12480 копеек или 124 р. 80 к. С каждой сотни рублей делается скидка в 20 рублей; с 24 р. 80 к. скидка округляется, эта сумма принимается за 25 рублей, и 20% от 25 составляет 5 рублей. Значит, скидка равна 25 рублям, и я уплачу 124 р. 80 к. - 25 р. = 99 р. 80 к. , т.е. получу не 16, а 20 копеек сдачи. Подведём итоги. Имея задачу на проценты, прежде всего, приводим её к одному из трёх основных типов. При этом не смущаемся, если «доля» оказывается больше самой величины. Затем задачи второго и третьего типов решаем «приведением к единице» (это, обычно, проще искусственных приёмов), а в задачах первого типа стараемся так разбить указанное число процентов на слагаемые или вычитаемые, чтобы было легче найти соответствующие им доли. |
