Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb.
|
3.5. Действия над приближёнными числами. ОкруглениеПри вычислениях с приближёнными числами возникают два вопроса: первый - как, имея данные приближённые числа, получить ответ с наибольшей возможной точностью; и второй - какую точность должны иметь исходные данные, чтобы ответ получился с наперёд указанной точностью. Каждый из этих вопросов может ставиться применительно к абсолютной и относительной погрешности. Таким образом, возникают четыре задачи, которыми занимается теория приближённых вычислений. Нас будет интересовать только один вопрос: как, исходя из данных приближённых чисел, получить ответ с нужной нам относительной погрешностью, затратив при этом наименьшие усилия. Мы увидим, что часто при этом все исходные данные приходится брать с одной и той же погрешностью, именно погрешностью наименее точного из данных чисел. Поэтому часто приходится более точное число сознательно заменять менее точным. Такая замена называется округлением приближённого числа. Если нам дано, например, приближённое число 27,136, а нам нужна точность до десятых, то мы «округлим» наше число, отбросив сотые и тысячные доли. Напишем: 27,136 ≈ 27,1 (знак ≈ означает приближённое равенство). Если нужно округлить 32,8 до целых единиц, то невыгодно просто отбросить десятые доли. Ошибка будет в восемь десятых; если же мы, отбросив десятые, увеличим цифру единиц на 1, т.е. напишем 32,8 ≈ 33, то ошибка будет всего в две десятых. Поэтому введено такое правило («правило округления»). Если крайняя левая из отбрасываемых при округлении цифр меньше пяти, то последнюю сохраняемую цифру не изменяют; если крайняя левая цифра (из отбрасываемых) больше пяти, или если она равна пяти, но за нею следуют ещё цифры, то последнюю сохраняемую цифру увеличивают на единицу. Если отбрасывается единственная цифра, равная пяти, то последнюю сохраняемую цифру оставляют без изменения, если она чётная, и увеличивают на единицу, если нечётная6. Обращаем внимание на одно обстоятельство, которое часто затрудняет неопытного счётчика. Округлим до сотых 10,297. Отбрасывая семёрку, мы должны цифру сотых увеличить на единицу. Но в нашем примере и без того имеется 9 сотых. В этом случае на месте сотых ставим нуль, а цифру десятых увеличиваем на единицу. Получим 10,30. Точно так же (округляем до десятых): 17,96 ≈ 18,0. Может случиться, что и вторая по очереди цифра даст при округлении десять, тогда переходим к следующей. Например (округляем до сотых) - 29,998 ≈ ≈ 30,00. Примеры (округляем везде до сотых долей): 10,237 ≈ 10,24; 2,2312 ≈ 2,23; 0,9852 ≈ 0,99; 0,985 ≈ 0,98; 0,315 ≈ ≈ 0,32. Примеры: Округлить до тысячных долей: 0,02836; 0,3385; 0,06253; 1,1335; 0,8339. Округлить, сохранив три верные цифры: 43,51; 285,51; 0,06835; 481,1; 61,45; 24832 (в этом примере нужно сохранить первые три цифры; нельзя, разумеется, просто написать 248, нельзя написать и 24800, так как эта запись покажет, что за отсутствие десятков и единиц мы ручаемся; следует написать 248∙102); 36,18; 2555. В предыдущей главе мы встречались с расчётами, в которых приходилось иметь дело сразу и с простыми, и с десятичными дробями. На практике обычно простые дроби заменяют десятичными, причем все десятичные дроби берут с некоторым приближением. Превратим, например,  в десятичную дробь, ограничиваясь точностью до тысячных долей. Делим 1 на 32:
Получаем ≈ 0,031Примеры: Превратить данные ниже простые дроби в десятичные, ограничиваясь точностью до тысячных долей: 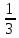 ;  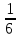;  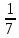;  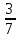;  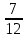;  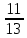;  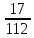;  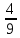;  ;  . |