Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb. Скачать 233.41 Kb.
|
3.3. Некоторые особенности записи приближённых чисел. Число верных знаков после запятойРезультат всякого измерения выражается числом, лишь приблизительно характеризующим измеряемую величину. Такими же числами являются исходные данные всех технических расчётов. Поэтому часто говорят, что техника имеет дело с приближёнными числами. Приближённые числа обычно даются в форме десятичных дробей. При этом последняя правая цифра характеризует величину абсолютной погрешности. Если в приближённых вычислениях мы имеем дело с числом 12,45, то это не значит, что величина, характеризуемая этим числом, не содержит тысячных долей. Можно только утверждать, что тысячные доли при измерении не учитывались; следовательно, абсолютная погрешность меньше одной сотой. Точно так же относительно приближённого числа 1,283 мы скажем, что абсолютная погрешность меньше одной тысячной. Приближённые числа принято записывать так, чтобы абсолютная погрешность не превышала единицы последнего десятичного разряда. Эту мысль выражают иногда иначе, именно говорят: абсолютная погрешность приближённого числа характеризуется числом десятичных знаков после запятой (один знак после запятой - абсолютная погрешность не превосходит одной десятой; два знака - одной сотой и т.д. ). Как же быть, если при тщательном измерении какой-нибудь величины получится, что она содержит целую единицу, две десятых, пять сотых, не содержит тысячных, а десятитысячные не поддаются учёту? Записать так: 1,25 нельзя - это будет значить, что тысячные не учтены, тогда как на самом деле мы уверены, что их нет. В этом случае принято ставить на месте тысячных нуль: 1,250. Таким образом, в учении о приближённых вычислениях числа 1,25 и 1,250 обозначают далеко не одно и то же. Первое число содержит тысячные; мы только не знаем, сколько именно. Второе - тысячных не содержит, сомнение вызывают только десятитысячные. Некоторые трудности возникают при приближённой записи больших чисел. Пусть число жителей села - ровно 2000 человек, а в большом городе - приблизительно 457000 жителей, причём относительно города мы ручаемся за тысячи, но допускаем, что ошиблись в счёте сотен и тем более - десятков и единиц. Как в самой записи отразить разницу между точным числом (в нашем примере 2000) и приближённым (457000)? Ведь нули на конце первого и на конце второго числа имеют разное значение: в первом случае они показывают на отсутствие сотен, десятков и единиц, во втором - на наше незнание числа сотен, десятков и единиц. Из этого затруднения выходят по-разному. Иногда неизвестные цифры приближённого числа заменяют маленькими нуликами (пишут 457000 вместо 457000); иногда пишут только верные цифры, а нули заменяют множителем, имеющим вид степени десяти: пишут 457∙103 вместо 457000. Мы будем придерживаться второго способа записи. Относительно числа 28300 будем утверждать, что нам точно известно отсутствие десятков и единиц, а относительно числа 32∙104 - что ни о тысячах, ни о сотнях, ни о десятках, ни о единицах мы ничего не знаем; известно только, что число содержит 32 десятка тысяч, т.е. что оно близко к 320000. Если мы ручаемся за сотни, но сомневаемся в десятках некоторого числа, то скажем, что число дано с точностью до сотен. Точно так же, ручаясь за тысячные доли, но сомневаясь в десятитысячных, скажем, что число дано с точностью до тысячных. Таким образом, мы можем одну и ту же мысль выразить тремя способами: про число 33,13 мы можем сказать, что оно дано с точностью до сотых; дано с двумя знаками после запятой; дано с абсолютной погрешностью 0,01. 3.4. Число верных цифр и его связь с процентной погрешностьюЧисло знаков после запятой или, лучше сказать, последний верный разряд - всё это связано с абсолютной погрешностью; а на практике особенно важна процентная погрешность. Посмотрим теперь, чем в записи приближённого числа характеризуется процентная погрешность. Сравним точность двух приближённых чисел, например, 1362,3 и 2,37. В первом абсолютная погрешность не больше одной десятой, во втором- она не превосходит одной сотой. Поэтому второе число выглядит более точным, чем первое. Подсчитаем процентную погрешность. В первом случае абсолютная погрешность меньше 0,1. Значит, процентная погрешность меньше  ; значит, она и подавно меньше ; значит, она и подавно меньше 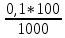 (уменьшив знаменатель, мы увеличиваем дробь). (уменьшив знаменатель, мы увеличиваем дробь).Итак, в первом случае процентная погрешность меньше, чем 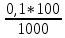 = 0,01%. Во втором случае абсолютная погрешность меньше 0,01, значит, процентная – меньше = 0,01%. Во втором случае абсолютная погрешность меньше 0,01, значит, процентная – меньше 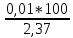 , т.е. подавно меньше , т.е. подавно меньше  = 1%. Мы видим, что второе число значительно менее точно, чем первое; первое в 100 раз точнее. Получается это потому, что в первом числе дано целых пять верных цифр, тогда как во втором - только три. = 1%. Мы видим, что второе число значительно менее точно, чем первое; первое в 100 раз точнее. Получается это потому, что в первом числе дано целых пять верных цифр, тогда как во втором - только три.Все цифры приближённого числа, в которых мы уверены, будем называть верными цифрами, независимо от их положения. Например, каждое из следующих пяти чисел имеет три верные цифры: 283∙105; 200∙102; 22,5; 0,0811; 2,10. Существует следующее правило: если число верных цифр больше или равно трём, то процентная погрешность равна единице, делённой на единицу со столькими нулями, сколько в приближённом числе верных цифр без трёх. Если же в приближённом числе две верные цифры, то процентная погрешность равна 10%. (Если дана одна верная цифра, то процентная погрешность может достигать нескольких десятков процентов; этот случай для практики не представляет интереса.) Например, процентная погрешность числа 2800∙102 не превосходит 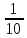 % (четыре верные цифры, значит, к единице приписываем один нуль); процентная погрешность числа 0,0028365 не превосходит % (четыре верные цифры, значит, к единице приписываем один нуль); процентная погрешность числа 0,0028365 не превосходит 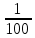 %; процентная погрешность числа 2,8 не превосходит 10%. Особенно важен случай, когда процентная погрешность равна 1%; большинство технических расчётов проводится именно с этой степенью точности. Эту степень точности даёт в производственной обстановке счетная линейка5. В этом случае приближённые числа должны иметь три верные цифры. В дальнейшем мы обратим особенное внимание на действие над приближёнными числами, имеющими три верные цифры. %; процентная погрешность числа 2,8 не превосходит 10%. Особенно важен случай, когда процентная погрешность равна 1%; большинство технических расчётов проводится именно с этой степенью точности. Эту степень точности даёт в производственной обстановке счетная линейка5. В этом случае приближённые числа должны иметь три верные цифры. В дальнейшем мы обратим особенное внимание на действие над приближёнными числами, имеющими три верные цифры.Примеры: Оценить процентную погрешность следующих приближённых чисел: 0,818; 2,410; 56∙105; 32,200; 0,00012; 843,356. |
