Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb. Скачать 233.41 Kb.
|
ГЛАВА IУСТНЫЙ СЧЁТ1.1. Общие замечанияКаждый из нас умеет считать в уме; в магазинах, в столовых, в трамвае - везде приходится иметь дело со счетом. Особенно важно уметь считать производственнику. Почти ни одна квалифицированная работа не обходится без предварительного подсчета. Одним приходится при этом возиться с карандашом и бумагой; другие считают в уме, но считают медленно, часто ошибаются и сильно устают; наконец, третьи считают легко и уверенно. Для того чтобы быстро и уверенно считать в уме, не нужно иметь ни специальных знаний, ни способностей. Несколько простых правил, а главное - постоянная тренировка в устном счете, - помогут научиться хорошо считать. Бывают люди, которые быстро множат и делят в уме четырех- и пятизначные числа. Достичь такого искусства трудно, надо помнить много правил, очень долго и утомительно тренироваться. Это искусство в практической жизни почти не может пригодиться. Наша задача - научиться работать с двузначными, иногда - с трехзначными числами. Этого для быта и производственной практики достаточно. Если же встретятся большие числа, то лучше, вернее, сделать вычисления на бумаге. Напомним некоторые арифметические термины. Числа, которые складываются, называются слагаемыми. Результат сложения называется суммой. То число, из которого мы вычитаем, называется уменьшаемым, число, которое мы вычитаем, называется вычитаемым, результат вычитания называется разностью чисел. Возьмем такой пример: 25-7=18. Здесь 25 - уменьшаемое, 7 - вычитаемое, 18 - разность. Числа, которые перемножаются, называются множителями или сомножителями. Иногда один из сомножителей называют множимым, другой - множителем, но такое различие несущественно: и множимое, и множитель совершенно равноправны. Результат умножения называется произведением. То число, которое делят на другое, называют делимым; то число, на которое делят, называют делителем. Результат деления называют частным. Разделим, например, 18 на 6. Получим 3. Здесь 18 - делимое, 6 - делитель, 3 - частное. Не всегда деление проходит так гладко. Поделим, например, 22 на 7. Получим 3 и в остатке единицу. Поделим остаток на 7, найдем одну седьмую. Значит 22:7=3 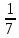 . Результатом деления целых чисел может быть дробное число (в нашем примере - целое с дробью). . Результатом деления целых чисел может быть дробное число (в нашем примере - целое с дробью).1.2. СложениеСкладывать в уме очень легко; и все-таки о сложении нужно сказать несколько слов. Ведь сложение - основное действие, поэтому складывать надо очень быстро и уверенно. Начнем с прибавления однозначного числа. Прибавить 5 к 23 совсем просто: будет 28. Важнее тот случай, когда единицы обоих слагаемых дают в сумме больше десятка и этот десяток нужно держать в уме. Прибавим, например, 8 к 87. Здесь лучше рассуждать так. В восьмидесяти семи не хватает до 90 тройки, а 8 равняется сумме 3 и 5. 87 да 3 - 90, да еще 5 - всего 95. Еще пример: 119+7. семь равно единице плюс шесть; 119 да единица - будет 120, да еще шесть - всего 126. Итак, однозначное слагаемое представляем в виде суммы двух меньших чисел, из которых одно дополняет большее слагаемое до целых десятков. Самая небольшая тренировка приводит к тому, что это разложение выполняется совершенно автоматически, без всякого усилия воли или внимания. Так же прибавляется число, состоящее из целого числа десятков или сотен. Прибавим, например, 50 к 272. Говорим: 272 да 30 даст 302, да еще 20 - всего 322. И здесь разбиваем слагаемое, состоящее из целых десятков, на два (50=30+20), одно из которых (30) дополняет десятки большего слагаемого (70) до целой сотни. Примеры: 326+9; 148+7; 94+8; 112+6; 243+80; 567+70; 192+20; 341+50; 1460+50; 277+70. Если оба слагаемых - многозначные числа, то к большему прибавляем сначала старший разряд меньшего, потом - младший разряд. Так, если прибавляется двузначное число, то сначала прибавляют десятки, потом единицы. Сложим, например, 343 и 25. Говорим: 343 да 20 будет 363, да еще 5 - всего 368. Так же поступают при сложении больших чисел. Если нужно сложить 8365 и 376, то рассуждают так: 8365 да 3 сотни, будет 8665, да семь десятков - 8735, да шесть единиц - всего 8741. Отметим случай, когда сложение упрощается. Если одно из слагаемых близко к целому числу десятков или сотен (вообще к «круглому» числу), то рассуждают так: пусть нужно сложить 173 и 59. 59 это 60 без единицы. Прибавляем еще 30 - будет 233, а нам нужно было прибавить 59, значит 1 нужно отнять; получится 232. Точно так же, если к 882 нужно прибавить 197, то говорим так: 197 это 200 без трех. 882 да 200 будет 1082, отнимая 3, получим 1079. Если оба числа близки к «круглым», например, если нужно сложить 98 и 395, то рассуждаем так: 98 - это 100 без двух: 365 - это 400 без пяти. 100 да 400 даст 500; отнимаем 2, будет 498, отнимем еще 5, будет 493. Это и есть искомая сумма. Примеры: 263+25; 384+49; 298+96; 4532+93; 882+161; 766+419; 89+77; 8122+891; 395+88. Если нужно сложить в уме несколько двузначных чисел, то, обычно сначала складывают все десятки, потом все единицы. Сложим, например, 26, 17, 85 и 43. Рассуждаем так. 20 да 10 будет 30, да еще 80 - будет 110, да 40 - всего 150; запоминаем. 6 и 7 дает 13, да 5 - будет 18, да еще 3 - всего 21. 150 да 21 - всего получится 171. Этот прием всегда быстро ведет к цели. Так же складываются и большие числа, например три или четыре трехзначных числа, но при этом приходится «держать в уме» несколько сумм, так что легко сбиться. Поэтому не тренированному человеку лучше большие числа складывать на счетах или на бумажке. Примеры: 56+13+18; 24+16+14+47; 39+48+13; 11+26+8+44; 58+43+92; 88+75+39. |
