Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb.
|
|
Процентом называется одна сотая часть данной величины. Если на заводе работает 2000 человек, то 20 человек составляют один процент (записывают: 1%) от всего количества работающих. Трудно представить себе область человеческой деятельности, в которой не пришлось бы иметь дела с процентами. В процентах выражают прирост населения, ход выполнения производственной программы; в процентах ведут учёт соцсоревнования; проценты выплачивают нам сберкассы. Поэтому, очень важно уметь быстро и безошибочно решать задачи, связанные с процентами. Простейшие задачи нужно научиться решать в уме. С процентами связаны три основных вида задач. Прежде всего, задачи, в которых дается некоторая величина и требуется найти другую величину, составляющую от данной указанное число процентов. Во-вторых, задачи, в которых даются две величины, и требуется узнать, сколько процентов от одной из величин составляет вторая. В-третьих, дается некоторое число и указывается, сколько процентов от искомой величины оно составляет; требуется найти саму величину. Прежде чем перейти к разбору этих трёх задач, обратим внимание на таблицу, помещённую на следующей странице. Эта таблица даёт соотношение между числами процентов некоторой величины и соответствующими её долями. Таблицу нужно помнить наизусть, если не целиком, то, во всяком случае, соотношения, отмеченные звёздочками.
Решим теперь задачу первого типа. На заводе 2140 рабочих, из них 30% мужчин. Сколько на заводе работает мужчин? Нужно, очевидно, найти 30% от числа 2140. – Тридцать - это 3∗10. Найдём сначала 10%, т.е. десятую часть. Это будет 214 человек. А 30% - в три раза больше. Умножаем 214 на 3, получаем 642. Значит, на заводе 642 мужчин. Вот ещё пример: норма выработки 225 деталей. Рабочий перевыполнил норму на 16%. Сколько деталей сделал он сверх нормы? Рассуждаем так: 16 это 4 раза 4. Найдём 4% и увеличим то, что получится, в 4 раза. Но 4% - это 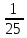 часть величины. Значит, нужно 225 разделить на 25. Получим 9. Умножив 9 на 4, получим 36. Значит, сверх нормы изготовлено 36 деталей.Переходим к задачам второго типа. У меня было 5 рублей, я израсходовал 3 рубля. Сколько процентов своих денег я израсходовал? Прежде всего, нужно определить, какую долю пяти составляет три. Так как каждый рубль составляет 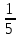 от пяти, то три рубля составят  . Значит, израсходовано три пятых всех денег.Если мы не запомнили правую половину таблицы (без звёздочек), то рассуждаем так. Каждая пятая часть составляет 20%. Значит, дадут 60%. Итак, израсходовано 60% имевшейся суммы.Более сложные задачи этого типа приводят обычно к делению на двузначное число. Мы их рассмотрим во второй главе. В заключение решим задачу третьего типа. В классе 6 отличников, что составляет 20% всего состава класса. Сколько в классе учеников? Рассуждаем так: 20% - это пятая доля. Пятая доля класса состоит из шести учеников. Значит, всего в классе 5∗6=30 учеников. Ещё пример. Забраковано 18 деталей, что составляет 2  % всей продукции. Сколько всего было изготовлено деталей? Если 2 % составляют 18 деталей, то 5% составляет 36 деталей, а 10% дадут 72 детали. Но 10% - это 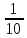 часть всей продукции. Значит, всего было изготовлено 72∗10=720 деталей.Примеры: Найти: 2% от 368, 3% от 720; 5% от 640; 12 % от 128; 4% от 725; 2 % от 40 (2 % это - половина от 5%); 1 % от 1400; 75% от 80; 50% от 3; 2 % от 240; 15% от 1280; 10% от 3, 5.Найти: какой процент (вместо «сколько процентов)) часто говорят «какой процент») составляет 8 от 10? 6 от 20? 100 от 1000? 10 от 50? 1 от 8? 9 от 50? 12 от 48? 1/2 от 1? 3 от 75? 10% какой величины равны трём? 5% какой величины равны семи? 25% какой величины равны 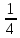 ? | ||||||||||||||||||||||||||||||||||||||||||||