Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb. Скачать 233.41 Kb.
|
1.9. Несколько слов о делении в умеДелить в уме значительно труднее, чем множить. Кроме случаев, упомянутых в начале главы (деление на 2, 4, 5, 25 и т.д.), стоит отметить только деление сравнительно небольших чисел на однозначное число. При этом приходится выполнять в уме те действия, которые мы привыкли делать на бумаге. Разделим, например, 95 на 7. Девять десятков дадут при делении на 7 один десяток, причём два десятка останутся неиспользованными. Эти два десятка да 5 единиц - всего 25 единиц - дадут при делении на 7 в частном 3 и в остатке - 4. Значит, ответ будет: 13 в частном и 4 в остатке, или 13 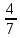 . .Примеры: 87:3; 126:3; 59:7; 97:2; 95:3; 147:7; 159:9; 90:11; 116:3; 104:13; 51:3; 91:7; 189:9; 89:9; 1000:3. В связи с делением стоит вопрос об отыскании той или иной доли данного числа. Действительно, чтобы найти половину какого-нибудь числа, например, 562, достаточно разделить его на 2. В нашем примере получим 281. Чтобы найти одну треть некоторого числа, нужно его разделить на 3. Умея делить в уме на 2, 4, 8, 5, 10, 25, 50, 100, 3, 6, 7, мы можем находить половину, четверть, восьмую, пятую, десятую и другие доли данного числа. Нетрудно найти двадцатую долю некоторого числа: для этого нужно разделить пополам его десятую долю. Найти три четверти какого-нибудь числа можно двумя способами: прежде всего, нужно найти одну четверть числа. Потом одно из двух: или умножить найденную четвертушку на 3, или отнять её от самого числа. Найдём, например, 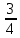 от 748. Делим 748 на 4. 700 пополам - 350, да 48 пополам - 24, всего 374. Полученное число делим ещё раз пополам: 300 пополам - 150, да 70 пополам - 35 (всего 185), да 4 пополам - 2, всего 187. Это - четвёртая часть. Делая первым способом, умножаем на 3: трижды сто - 300, да трижды 80 – 240 (всего 540), да трижды семь - 21; всего 561. Делая вторым способом, отнимаем найденную четвертушку (187) от самого данного числа (748). Вычитаемое близко к круглому числу (к 200), недостаёт только тринадцати. Прибавляем к уменьшаемому 13, получаем 761; отнимаем двести - остаётся 561. от 748. Делим 748 на 4. 700 пополам - 350, да 48 пополам - 24, всего 374. Полученное число делим ещё раз пополам: 300 пополам - 150, да 70 пополам - 35 (всего 185), да 4 пополам - 2, всего 187. Это - четвёртая часть. Делая первым способом, умножаем на 3: трижды сто - 300, да трижды 80 – 240 (всего 540), да трижды семь - 21; всего 561. Делая вторым способом, отнимаем найденную четвертушку (187) от самого данного числа (748). Вычитаемое близко к круглому числу (к 200), недостаёт только тринадцати. Прибавляем к уменьшаемому 13, получаем 761; отнимаем двести - остаётся 561.Второй приём годится во всех случаях, когда числитель искомой доли на единицу меньше знаменателя, а первый во всех без исключения случаях. Значит, первый приём более общий, зато второй - в тех случаях, когда он пригоден - немного проще. Вычислим первым приёмом 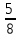 от 344. Находим от 344. Находим 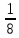 ; для этого делим 344 на 8. Сначала делим 344 пополам - получаем 172; делим ещё раз пополам - получаем 86, делим ещё раз пополам - получаем 43. Это - одна восьмая доля от 344. А нам нужно 5 таких долей. Остаётся умножить 43 на 5. 43 на 10 - 430. Делим пополам-215. Значит, ; для этого делим 344 на 8. Сначала делим 344 пополам - получаем 172; делим ещё раз пополам - получаем 86, делим ещё раз пополам - получаем 43. Это - одна восьмая доля от 344. А нам нужно 5 таких долей. Остаётся умножить 43 на 5. 43 на 10 - 430. Делим пополам-215. Значит, 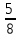 от 344 составят 215. от 344 составят 215.Вычислим (вторым приёмом) 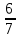 от 1449. Одна седьмая от 1449 равна 207 (1449=14 сотен, да ещё 49; 14 сотен дают при делении на 7 две сотни, а сорок девять при делении на семь даёт 7). Остаётся отнять 207 от 1449. Получаем 1242. Это и есть искомая доля. от 1449. Одна седьмая от 1449 равна 207 (1449=14 сотен, да ещё 49; 14 сотен дают при делении на 7 две сотни, а сорок девять при делении на семь даёт 7). Остаётся отнять 207 от 1449. Получаем 1242. Это и есть искомая доля.Примеры: Найти 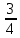 от 1972; от 1972; 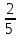 от 1035; от 1035; 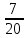 от 5420; от 5420; 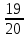 от 3340; от 3340; 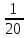 от 837; от 837; 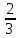 от 5343; от 5343; 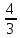 от 711 (лучше всего поступать так: найти одну треть от 711 и прибавить ее к 711); от 711 (лучше всего поступать так: найти одну треть от 711 и прибавить ее к 711); 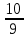 от 387 (как в предыдущем примере); от 387 (как в предыдущем примере); 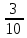 от 6812. от 6812.1.10. Проценты |
