Берман. Государственное издательство техникотеоретической литературы
 Скачать 233.41 Kb.
|
3.12. Извлечение корней из чисел с тремя верными цифрамиНачнём с извлечения корней из чисел, больших единицы, но меньших 100. Извлечём, папример, квадратный корень (с тремя верными цифрами) из 79,3. В таблице квадратов этого числа нет, но есть близкое к нему: 81. Корень из 81 равен 9. Будем считать первым, совсем грубым значением нашего корня, число 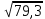9:  ≈ 9.Делим данное число (79,3) на это первое приближение, в частном берём только две цифры:
Складываем делитель (9) и частное (8,8) и делим сумму пополам. Получим второе приближение. В записи это будет выглядеть так:
Второе приближение берём с тремя верными цифрами. Делим подкоренное число на второе приближение (частное берём с тремя верными цифрами). Складываем опять делитель и частное и делам сумму пополам. Полученное третье приближение и даст нам искомый корень:
Искомый корень равен 8, 90. Рассмотрим ещё пример. Извлечём корень из 41,5. Из таблицы квадратов видим, что искомый корень лежит между шестью (6∗6=36) и семью (7∗7=49). Но 41,5 не очень близко ни к 36, ни к 49. Поэтому возьмём в качестве первого приближения 6,5 (на практике чаще всего в качестве первого приближения приходится брать не целое число, как было у нас в первом примере, а целое число с половиной). Далее располагаем действие так:
 Примеры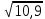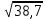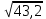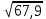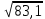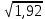:  ;  ;  ;  ;  ;  ;  ;  ;  ;  ;(Проверить себя, возведя полученные результаты в квадрат.) Рассмотрим теперь извлечение корня из произвольных чисел, но корень попрежнему будем искать с тремя верными цифрами. Поэтому данное число тоже будем округлять так, чтобы в нём оставалось три верные цифры. Если дано число, имеющее 2 верные цифры, то и в ответе нужно будет оставить только две цифры: третья будет сомнительной. Округлив число, разбиваем его на грани, по две цифры в каждой, начиная от запятой в обе стороны (в первой и последней грани может получиться по одной цифре). Вот примеры такой «предварительной обработки» подкоренного числа; грани отделяем запятыми, поставленными сверху («апострофами»):  ≈  =  . ≈  =  (если число целое, то подразумеваем запятую в конце его). 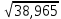 ≈  . ≈  =  .Отбрасываем теперь все нули и вместо апострофа ставим запятую (снизу). В первом примере получим » 4,83. Во втором » » 26,4. В третьем » » 39,0. В четвёртом » » 56,5. Из полученного числа извлекаем корень, как из числа, заключённого между единицей и сотней. Запятую ставим, руководствуясь следующим правилом: если в подкоренном числе есть цифры левее запятой, то в корне будет столько цифр левее запятой, сколько в подкоренном числе было граней до запятой. Если же перед занятою имеется только нуль, то после запятой будет столько нулей, сколько в подкоренном числе после запятой было граней, состоящих сплошь из нулей. В первом нашем примере будем иметь: ≈ = 0, ∗∗∗(Перед запятой только нуль; граней после запятой, состоящих сплошь из нулей, тоже нет. Сразу после запятой дойдут отличные от нуля цифры, обозначенные звёздочками.) Во втором примере: ≈ = ∗∗∗-10(До запятой четыре грани. Значит, в корне должно быть четыре цифры до запятой. Мы найдём только три из них. Нужно либо приписать справа нуль, либо помножить результат на 101=10.) В третьем примере: 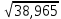≈  = ∗,∗∗(одна грань до запятой в подкоренном числе, одна цифра до запятой в корне.) В четвёртом примере: ≈ = 0,00∗∗∗(После запятой имеются две грани, состоящие сплошь из нулей. Значит, корень будет содержать два нуля после запятой.) Сделаем один пример полностью. Найдём квадратный корень из 0,0003387. «Обрабатываем» подкоренное число: 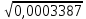 ≈  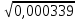=  = 0,00∗∗∗Извлекаем теперь корень из 3,39. Первым приближением может служить 2, так как 3,39 близко к 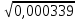4.
= 0,0184Если нужно извлечь приближённый корень из точного числа, например, из двух, то дописываем столько нулей, чтобы получилось три цифры. Так, в указанном примере пишем: 2=2,00. Дальше поступаем обычным порядком; два больше 1, но меньше четырёх. Значит,  заключено между 1 и 2. Возьмём первым приближением 1,5:
= 1,41.О том, как извлекать корни больше чем с тремя верными цифрами, говорить в этой книге нет возможности. Соответствующие правила есть в любом учебнике алгебры, но они значительно сложнее изложенных здесь. Примеры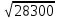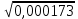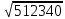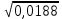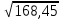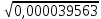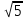:  ;  ;  ;  ;  ;  ;  ;  ;  ;  ;  ;  . (В трёх последних примерах подкоренное число дано точно.) |