Мои лекции по Грачеву. РС-71. Грачев Николай Николаевич Список литературы
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
Возмущающие силы.Возмущающие силы не зависят от движения системы, но активно влияют на него. Существует 2 способа задания возмущающих воздействий:
Различают 2-е задачи виброизоляции (в соответствии с заданием сил):
Активная виброизоляция.Основным в данной задаче является изоляция источника вибрации от аппаратуры.
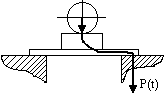
Пассивная виброизоляция.Пассивная виброизоляция – изоляция аппаратуры от вибрирующего основания.
Часто по определенным амплитудам блока рассчитывают ускорения элементов конструкций. Рассчитанное ускорение сравнивается с допустимым. Если оно меньше или равно допустимому, то система спроектирована верно, если больше, то необходимо внести коррективы в систему амортизации. Постановка задачи такова: спроектировать систему амортизации, при 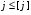 . .Энергетические соотношения в системе виброизоляцииции.Допустим, существует система c S степенями свободы.
aij - инерционный (кинетический) параметр системы
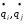 - обобщенные скорости по соответствующим координатам (скорости абсолютные). - обобщенные скорости по соответствующим координатам (скорости абсолютные).
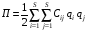 Сij – жесткостной параметр системы: 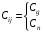 qi, qj – деформации упругих элементов (относительные).
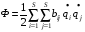 bij – коэффициент демпфирования. 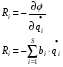
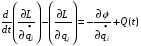 I II III L=T-П - функция Лагранжа. i – число обобщенных координат, равное числу степеней свободы. I - баланс кинетической и потенциальной энергии в системе. II - потери энергии на диссипацию. III - приток энергии за счет возмущающих сил. В частных случаях Q(t) равно нулю:
Данное уравнение позволяет проанализировать движение системы с любой степенью свободы и в любой момент времени. Для системы c S степенями свободы уравнение Лагранжа превращается в систему из S дифференциальных уравнений. При S=6 уравнение Лагранжа – система из 6-ти уравнений. Решение в общем виде подобной системы – сложная задача даже при использовании ЭВМ. При S = 1 - система решается. При S > 1 – применяются упрощенные методы расчета системы.
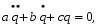 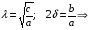 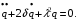 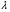 - частота собственных колебаний системы. - частота собственных колебаний системы.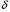 - коэффициент затухания. - коэффициент затухания.с - жесткостной параметр системы. а - инерционный параметр системы. Существуют два случая:
Т.к. обычно 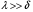 на практике логарифмический декремент Колебаний: на практике логарифмический декремент Колебаний: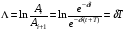 Примечания:
Рассмотренные случаи соответствуют установке виброизоляторов с вязким трением или гистерезисными потерями, для которых справедлива функция: 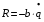 . .
T – период собственных колебаний. Решение выглядит следующим образом:
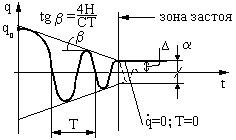
Основные особенности движения систем на амортизаторах с сухим трением.
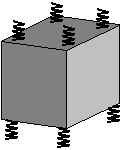
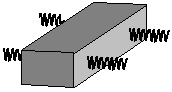
Остановка блока в зоне застоя происходит в момент времени t1, для которого 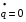 и и 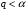 (при (при 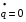 ); );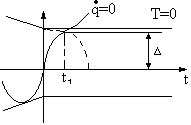 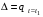 . .Наличие зоны застоя объясняется малой величиной потенциальной энергии, которая не может преодолеть силы сухого трения амортизаторов; кинетическая энергия равна нулю. Говорят, что амортизатор для зоны застоя закрыт. Амортизаторы с сухим трением не работают при амплитудах смещения 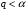 . .Вынужденные колебания системы при пассивной виброизоляции. Блок установлен на условном амортизаторе.
При вибрации основания происходит перемещение блока. Нам необходимо определить параметры колебания блока: D = ?; 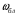 =?; =?;Рассмотрим систему с одной степенью свободы. Решение получается при помощи уравнения Лагранжа.
Уравнение Лагранжа имеет следующий вид: 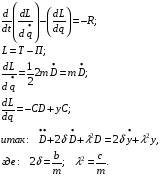 Вынужденные колебания системы виброизоляцииции описываются неоднородными дифференциальными уравнениями второго порядка. Искомая амплитуда D является решением этого уравнения. Это сумма решений однородного и частного решения неоднородного уравнения, т.е. D = D0 + D1 D0 – решение однородного дифференциального уравнения. D1 – частное решение неоднородного уравнения. Для получения D0 правая часть уравнения приравнивается к нулю. Т.о. получаем уравнение, которое описывает свободное движение объекта. Ввиду быстрого затухания свободных колебаний в практических случаях можно не учитывать D0 , тогда D= D1 и искомое решение получается в виде частного решения этого уравнения: 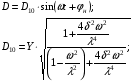 введем обозначения: 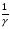 - коэффициент динамичности. - коэффициент динамичности.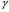 - коэффициент виброизоляции. - коэффициент виброизоляции. Отношение статической упругой силы к амплитуде силы возбуждающих колебаний: 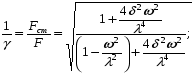 Т.о. 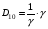 , т.е. взаимосвязь между амплитудой вибрации блока и амплитудой вибрации основания описывается коэффициентом динамичности. Коэффициентом динамичности показывает во сколько раз амплитуда вибрации блока больше (или меньше) амплитуды вибрации основания. Для защиты блока необходимо выполнение следующего соотношения: , т.е. взаимосвязь между амплитудой вибрации блока и амплитудой вибрации основания описывается коэффициентом динамичности. Коэффициентом динамичности показывает во сколько раз амплитуда вибрации блока больше (или меньше) амплитуды вибрации основания. Для защиты блока необходимо выполнение следующего соотношения: 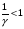 . .Частота вынужденных колебаний блока равна частоте возмущающих воздействий. Амплитуда вибраций блока определяется соотношением 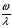 , т.е. соотношения возмущающего воздействия и собственной частоты системы. , т.е. соотношения возмущающего воздействия и собственной частоты системы.Вынужденные колебания системы амортизации при пассивной виброизоляции. Блок установлен на условном амортизаторе.
При вибрации основания происходит перемещение блока. Нам необходимо определить параметры колебания блока: D = ?; 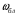 =?; =?;Рассмотрим систему с одной степенью свободы. Решение получается при помощи уравнения Лагранжа.
Уравнение Лагранжа имеет следующий вид: 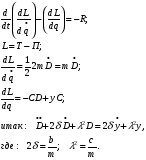 Вынужденные колебания системы амортизации описываются неоднородными дифференциальными уравнениями второго порядка. Искомая амплитуда D является решением этого уравнения. Это сумма решений однородного и частного решения неоднородного уравнения, т.е. D = D0 + D1 D0 – решение однородного дифференциального уравнения. D1 – частное решение неоднородного уравнения. Для получения D0 правая часть уравнения приравнивается к нулю. Т.о. получаем уравнение, которое описывает свободное движение объекта. Ввиду быстрого затухания свободных колебаний в практических случаях можно не учитывать D0 , тогда D= D1 и искомое решение получается в виде частного решения этого уравнения: 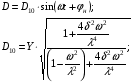 введем обозначения: 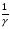 - коэффициент динамичности. - коэффициент динамичности.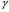 - коэффициент виброизоляции. - коэффициент виброизоляции. Отношение статической упругой силы к амплитуде силы возбуждающих колебаний: 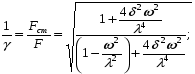 Т.о. 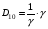 , т.е. взаимосвязь между амплитудой вибрации блока и амплитудой вибрации основания описывается коэффициентом динамичности. Коэффициентом динамичности показывает во сколько раз амплитуда вибрации блока больше (или меньше) амплитуды вибрации основания. Для защиты блока необходимо выполнение следующего соотношения: , т.е. взаимосвязь между амплитудой вибрации блока и амплитудой вибрации основания описывается коэффициентом динамичности. Коэффициентом динамичности показывает во сколько раз амплитуда вибрации блока больше (или меньше) амплитуды вибрации основания. Для защиты блока необходимо выполнение следующего соотношения: 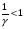 . .Частота вынужденных колебаний блока равна частоте возмущающих воздействий. Амплитуда вибраций блока определяется соотношением 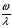 , т.е. соотношения возмущающего воздействия и собственной частоты системы. , т.е. соотношения возмущающего воздействия и собственной частоты системы.Коэффициент динамичности. Вид кривой зависит от демпфирования системы. 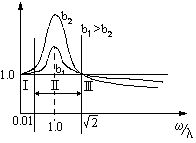 1 зона. Она характеризуется 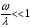 , что соответствует жесткой системе с высокими собственными частотами без амортизаторов. Для этого случая , что соответствует жесткой системе с высокими собственными частотами без амортизаторов. Для этого случая 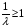 защиты от вибрации нет. В лучшем случае параметры вибрации полностью передаются на блок без усиления. защиты от вибрации нет. В лучшем случае параметры вибрации полностью передаются на блок без усиления.2 зона. Зона резонанса. Она характеризуется примерным равенством частот и 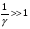 . Для реальных виброизоляторов . Для реальных виброизоляторов 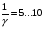 . Зона резонанса недопустима. Уменьшение . Зона резонанса недопустима. Уменьшение 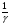 возможно за счет увеличения демпфирования как амортизаторов, так и системы в целом. возможно за счет увеличения демпфирования как амортизаторов, так и системы в целом.3 зона. Зарезонансная зона. 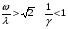 часто часто 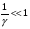 здесь имеет место защита от вибраций. Зона соответствует малым значениям 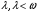 и соответствует системе с амортизаторами. и соответствует системе с амортизаторами.Т.о. задача проектирования системы амортизации сводится к обеспечению таких значений 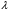 , чтобы , чтобы 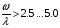 , при этом , при этом 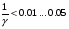 , т.е. ослабление вибрации в 100 раз. , т.е. ослабление вибрации в 100 раз.Значительное уменьшение собственных частот, приводящее к увеличению значения 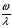 и соответственно к еще большему уменьшению и соответственно к еще большему уменьшению 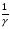 во многих случаях не оправдано, т.к. при этом резко увеличиваются габариты и стоимость амортизаторов. во многих случаях не оправдано, т.к. при этом резко увеличиваются габариты и стоимость амортизаторов.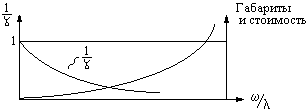 Основные этапы проектирования системы амортизации:
а) 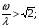 - работа в зарезонансной зоне. - работа в зарезонансной зоне.б) 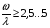 Если а) и б) выполнено, то:
при 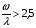 б) сразу принимаем решение о том, что система спроектирована правильно. б) сразу принимаем решение о том, что система спроектирована правильно.
Фазо-частотная зависимость. 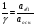 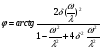 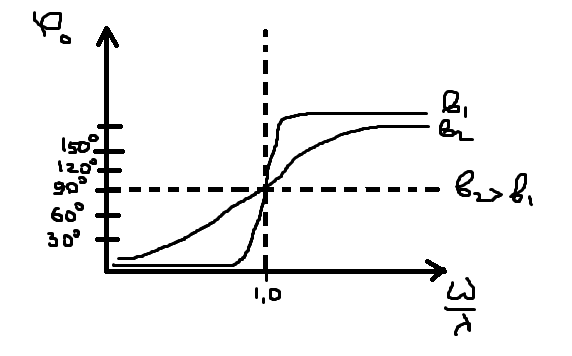 Эффективность амортизации.
Эффективность оценивается только в зарезонансной области. Особенности движения системы с 6 степенями свободы. Парциальные частоты системы.  Парциальные системы: Если в системе амортизации с 6-ю степенями свободы зафиксировать 5 степеней, то оставшаяся степень будет характеризоваться своей парциальной частотой. Т.о. для системы из 6-ти парциальных частот три частоты определяют поступательное движение объекта вдоль оси координат X, Y, Z и три частоты определяют поворотное движение объекта вокруг координат X, Y, Z. 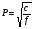 , где P – парциальная частота. , где P – парциальная частота. Парциальные частоты в поступательные:
Парциальные частоты поворотные:
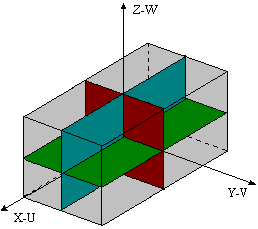
Как видно из формул, расчет этих частот не представляет труда, если известны параметры системы. Неравенство Релея: 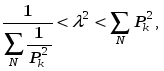 где 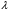 – собственная частота системы. – собственная частота системы.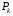 – одна из 6-ти парциальных частот: – одна из 6-ти парциальных частот: 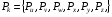 под знаком суммы могут присутствовать только разные парциальные частоты.  – количество слагаемых, которое зависит от конструктивных особенностей системы амортизации, как справа, так и слева участвуют одни и те же парциальные частоты. – количество слагаемых, которое зависит от конструктивных особенностей системы амортизации, как справа, так и слева участвуют одни и те же парциальные частоты.Неравенство Релея позволяет определить диапазон собственных частот системы без точного определения конкретных частот, причем чем больше N, тем меньше точность в определении частот. Расширение диапазона собственных частот при расчете по неравенству Релея обеспечивает дополнительный запас по значению коэффициента динамичности. 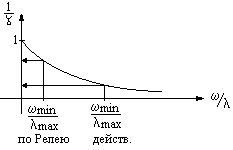 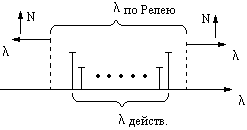 Конструктивные особенности системы амортизации. Основной особенностью, определяющей вид неравенства Релея, является наличие плоскости в системе. Плоскость симметрии – это плоскость, относительно которой симметричны:
Различаются следующие системы амортизации:
Различные системы имеют различный вид неравенства Релея и различную точность в определении частот. Система 3-мя плоскостями симметрии.
Система с 4-мя амортизаторами Zi = 0. т.е. установка виброизоляторов в плоскости XOY. Свойства: при строгом решении исходной системы 6-ти дифференциальных уравнений подобной системы амортизации наличие плоскости симметрии масс частей блоков, координат установки амортизаторов, жесткостные параметры амортизации приводит к тому, что указанная система уравнений разбивается на 6 независимых уравнений. Из каждого уравнения может быть точно определена своя собственная частота.
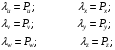 это вырожденное неравенство Релея-Донкерли для N = 1. 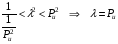 Т.о. на оси частот имеем 6 дискретных собственных частот. Во всех случаях желательно сужать диапазон собственных частот. В данной системе амортизации возможно при введении дополнительных условий добиться равенства всех собственных частот: 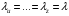 и на оси частот имеем одну дискретную частоту. и на оси частот имеем одну дискретную частоту.Эти дополнительные условия имеют вид: а) Динамические жесткости виброизоляторов и соответствующие системы амортизации по всем направлениям должны быть равны: Cgu = Cgv = Cgw. б) Координаты «Х» виброизоляторов должны быть равны радиусу инерции относительно оси «Y», а координаты «Y» виброизоляторов должны быть равны радиусу инерции относительно оси «Х». 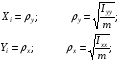 Недостаток: для большинства амортизаторов: Cgu = Cgv 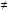 Cgw. Cgw. |

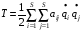
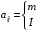
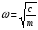
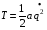 ,
, 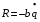
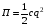 ,
, 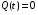
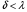
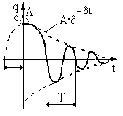
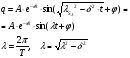
 - угол отсечки.
- угол отсечки. . Характер движения апериодический. В системах виброизоляцииции практически не встречается.
. Характер движения апериодический. В системах виброизоляцииции практически не встречается.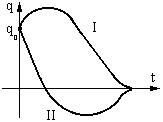
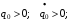
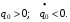
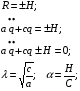
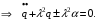
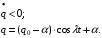
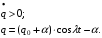
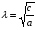 и не зависит от величины диссипативных сил.
и не зависит от величины диссипативных сил. , т.е. существует некоторая амплитуда смещения блока относительно положения равновесия.
, т.е. существует некоторая амплитуда смещения блока относительно положения равновесия. 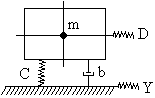
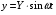
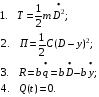
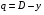 - с учетом сжатия с обоих концов.
- с учетом сжатия с обоих концов.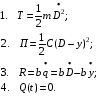
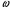 - задано.
- задано.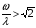 а) рассчитываем
а) рассчитываем 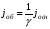
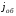 и
и 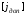 – ускорение объекта и допустимое ускорение. При
– ускорение объекта и допустимое ускорение. При 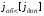
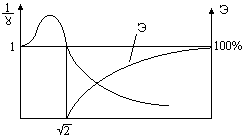
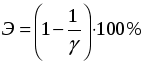

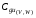 – суммарные динамические жесткости системы;
– суммарные динамические жесткости системы;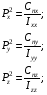
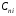 – поворотные жесткости.
– поворотные жесткости.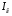 – момент инерции центральных осей блока.
– момент инерции центральных осей блока.