|
|
ТСП 11. I источники энергии для сварки глава физические основы и классификация сварочных процессов
Пример 2.1. Определить дебаевский радиус экранирования для высокоионизованной плазмы сварочной дуги при условиях: р = 105 Па, Т = 104К,nе =1024м-3.
Решение. Подставив числовые данные в формулу (2.8), получим
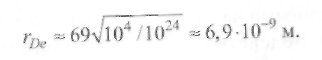
Для данного случая только в кубике газа со стороной менее
√2 • 6,9 х 10-9 м ≈ 11 нм можно определить разность концентраций ионов и электронов. Поэтому можно сделать вывод: в сварочной дуге при атмосферном давлении плазма квазинейтральна.
Дебаевское экранирование является статистическим понятием и имеет место только в том случае, когда в заряженном облаке находится достаточно много частиц. Очевидно, что если облако состоит только из одной или двух заряженных частиц, то дебаевское экранирование не применимо. Используя выражение (2.8), можно вычислить число частиц NDe в «дебаевской сфере»:
(2.10)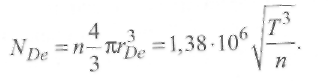
Чтобы плазма имела коллективные свойства, помимо неравенства (2.9) должно выполняться условие
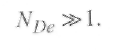 (2.11) (2.11)
Специфические особенности плазмы могут проявляться только тогда, когда распределение заряженных частиц в ней становится неоднородным и возникают макроскопические электромагнитные поля. Электромагнитные поля в плазме могут создаваться и внешними источниками, однако существенно, что эти поля влияют на характер распределения и движение заряженных частиц в плазме, индуцируя в ней заряды и токи, которые, в свою очередь, сами создают электромагнитные поля, изменяя полное электромагнитное поле в системе. Происходит так называемое самосогласованное воздействие заряженных частиц и электромагнитного поля друг на друга. Собственно, в этом и проявляются коллективные свойства плазмы.
2.2.3. Идеальная плазма. Плазменный параметр
Принято различать идеальный и реальный газы. Критерием идеальности является малость средней потенциальной энергии частиц по сравнению с их средней кинетической (тепловой) энергией. Аналогичный критерий идеальности применим и к плазме.
В приведенном выше определении плазмы она была охарактеризована как газ, состоящий из заряженных частиц. Взаимодействие между заряженными частицами подчинено закону Кулона. Для кулоновского взаимодействия частиц критерий идеальности записывается в виде e2/rср
e2n1/3«kT. С этим выражением связана следующая важная характеристика плазмы:
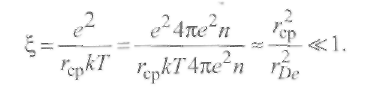 (2.12) (2.12)
Здесь величина ξ, называется плазменным параметром, и условие применимости газового приближения плазмы (идеальной плазмы) сводится к требованию ξ«1. Неравенство (2.12) означает, что среднее расстояние между заряженными частицами в плазме должно быть значительно меньше дебаевского радиуса экранирования.
Таким образом, критерий идеальности плазмы, т. е. малость энергии кулоновского взаимодействия по сравнению с кинетической (тепловой) энергией, совпадает с условием применимости дебаевского экранирования - число заряженных частиц внутри сферы радиусом rDe должно быть велико. В плазме газовых разрядов неравенство (2.12) выполняется с большим запасом: ξ ≤ 10-2 .
Вследствие высоких температур плотность частиц в сварочной плазме, несмотря на сравнительно высокие давления р, настолько мала, что практически для нее можно считать справедливыми уравнения идеального газа, в том числе уравнение, выражающее основной закон газового состояния для 1 моль газа,
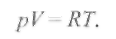 (2.13) (2.13)
Его удобно записать в виде
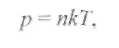 (2.14) (2.14)
где n = nе + ni + nα ; k= R/N; n = N/V; R = 8,31 Дж/(моль • К) - универсальная газовая постоянная; N = 6,02- 1023 моль-1 - число Авогадро.
При атмосферном давлении (р = 105 Па) получим зависимость концентрации частиц от температуры:
n= ρ/kT = 7,34 • 1027/T Если T = 300 K, то n = 7,34 • 1027/300 ≈ 2,7 • 1025м-3.
Это так называемое число Лошмидта. В плазме сварочной дуги при р = 105 Па и Т = 6000 К, несмотря на ионизацию, общее число частиц в 1 м3 уменьшится почти в 20 раз, т. е. n ≈ 1,2 • 1024 м-3 .
Отступления от модели идеального газа для плазмы связаны с двумя явлениями, существующими только при больших концентрациях заряженных частиц: электрическим взаимодействием между ними и так называемым вырождением.
2.2.4. Эффективное сечение взаимодействия
После возбуждения разряда ионизация в газе может происходить в основном двумя путями: взаимным соударением частиц и поглощением квантов энергии (фотоионизация). Одновременно идут процессы деионизации, т. е. образование нейтральных частиц при взаимодействии положительных ионов и электронов.
Для характеристики вероятности столкновений частиц в газе служат такие величины, как длина свободного пробега частицы Λ, среднее время пробега τ = Λ /v и частота столкновений частиц v = 1/ τ.
Мерой вероятности индивидуального акта определенного рода (например, упругого соударения, ионизации и т. д.) является соответствующее эффективное сечение Q, которое для обычных газов часто называют газокинетическим:
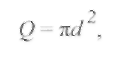 (2.15) (2.15)
где d - диаметр частицы.
Чтобы произошло столкновение, центры молекул должны находиться на минимальном расстоянии, равном диаметру d частицы. Принимая модель упругих шаров, можно построить схему для определения Q (рис. 2.7), из которой следует геометрический смысл эффективного сечения Q - это площадь круга радиусом, равным сумме радиусов сталкивающихся частиц. С учетом движения обеих частиц при равновесном распределении скоростей принимают Q=√2πd2.
Длина свободного пробега частиц Λ зависит как от Q, так и от n- концентрации частиц в 1 м3 . С одной стороны, определяя относительную долю площади, занятой частицей, через слой газа единичной площади толщиной dx (рис. 2.8), получим вероятность соударения на длине dx, равную nQ dx /1. С другой стороны, вероятность столкновения частиц при малом dxсоответствует отношению толщины слоя dx к длине свободного пробега Λ и равна dx/ Λ.
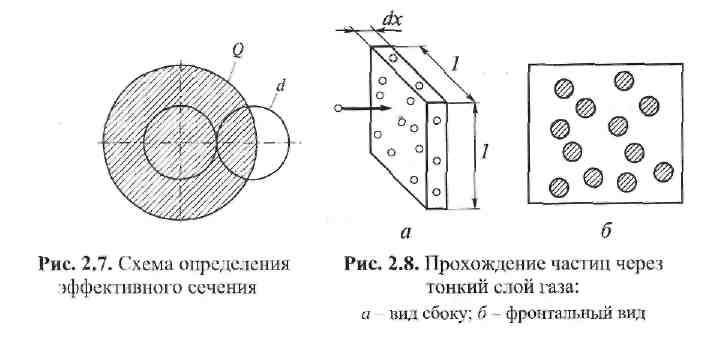
Следовательно, dx/Λ = nQdx/l, откуда
(2.16)
и
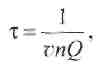
(2.17)
где v - скорость частиц.
Оказывается, что для молекул газокинетическое сечение Q мало зависит от их энергии (при высоких температурах). В то же время, чем больше размеры частиц, тем меньше длина их свободного пробега. Кроме того, согласно уравнению Клапейрона - Менделеева, длину свободного пробега можно выразить так:
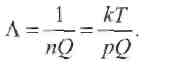
Подставляя в (2.18) значение k= 1,38 • 10 Дж/К и ρ =1,01 • 105 Па,
получаем
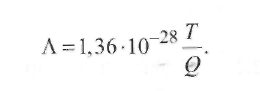 (2.19) (2.19)
Иногда в литературе эффективное сечение приведено не для одной пары частиц, а для 1 м3 газа. Тогда его обозначают S и считают, что
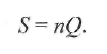 (2.20) (2.20)
Наличие сил кулоновского взаимодействия между электронами и ионами делает их соударения в плазме значительно более сложными, чем соударения нейтральных частиц в газе. Вместо зигзагообразной траектории броуновского движения молекул траектория заряженной частицы становится извилистой (более сглаженной), соответствующей изменениям (флуктуациям) электрического поля в плазме. Поэтому в плазме, вообще говоря, следует учитывать все возможные эффективные сечения при соударениях:
ион - атом Qia(перезарядка)
ион - ион Qii (сечение Гвоздовера)
электрон - атом Qea (сечение Рамзауэра)
электрон - ион Qei(прилипание или захват электрона)
электрон - электрон Qee
Тогда для k сортов частиц длина свободного пробега электрона
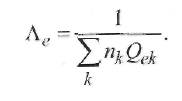
Однако практически в сварочных дугах достаточно учитывать только эффективное сечение Qea или Qe = Qea + Qei, так как другие эффективные сечения сравнительно малы.
Упругие столкновения электронов с нейтральными атомами Должны быть описаны с позиций квантовой механики. Полное решение квантово-механической задачи удается получить лишь для Простейших атомов - атомов водорода и гелия. Для более сложных атомов обычно используют экспериментальные данные. В большинстве случаев наибольшее эффективное сечение Qea имеет место при приближении скорости электронов к нулю. В диапазоне малых энергий электронов (1...5 эВ) с увеличением их энергии Qea, как правило, уменьшается.
2.2.5. Эффект Рамзауэра
Обращает на себя внимание резкое уменьшение эффективного сечения Qea при малых энергиях электронов (ε ≤ 1 эВ) для ряда тяжелых атомов, в том числе для атомов тяжелых инертных газов. Это явление называется эффектом Рамзауэра (рис. 2.9).
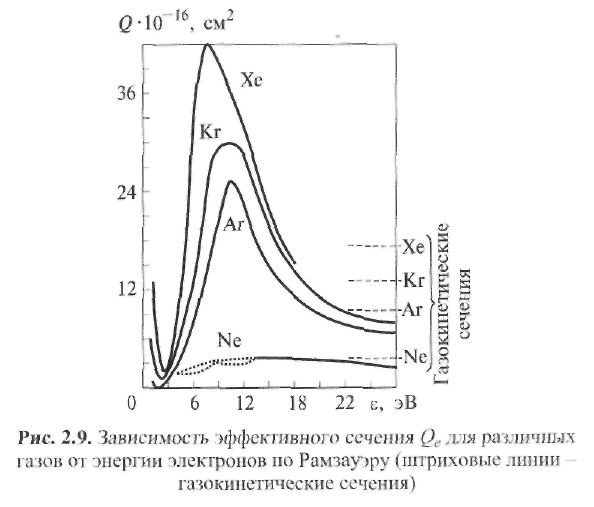
При малых энергиях электронов в тяжелых инертных газах взаимодействие электронов с атомами сильно ослабляется в связи с эффектом Рамзауэра. Это объясняется волновым характером поведения электрона в процессе его упругого взаимодействия. При определенном соотношении между длиной волны де Бройля
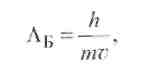
(2.21)
соответствующей медленно движущемуся электрону, и размерами атома создаются условия для почти беспрепятственного прохождения волны через атом, что дает малое сечение Qea. (Здесь h= 6,626 • 10-34 Дж • с - постоянная Планка).
В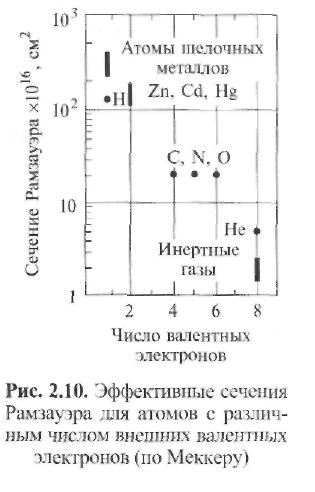 условиях обычных сварочных дуг при температуре в столбе дуги Tст = 5000... 12 000 К значения полных сечений Рамзауэра Qe = Qea + Qei, вычисленные Меккером, составляют от (2...5)• 10-16 см2 для инертных газов и до 5 • 10-14 см2 для щелочных металлов (рис. 2.10), т. е. отличаются почти в 200 раз. условиях обычных сварочных дуг при температуре в столбе дуги Tст = 5000... 12 000 К значения полных сечений Рамзауэра Qe = Qea + Qei, вычисленные Меккером, составляют от (2...5)• 10-16 см2 для инертных газов и до 5 • 10-14 см2 для щелочных металлов (рис. 2.10), т. е. отличаются почти в 200 раз.
Возникает вопрос: когда и какие именно значения длины свободного пробега или эффективного сечения следует применять в расчетах?
Из рис. 2.9 следует, что эффект Рамзауэра и минимум сечения Se = nQe соответствуют энергиям электрона ≈ 1 эВ.
В плазме столба сварочной дуги при ТCT = 5000... 10 000 К, как будет показано ниже, средняя энергия электронов в соответствии с масвелловским распределением по скоростям равна ≈ 1 эВ. Поэтому для плазмы в инертных газах следует принять длину свободного пробега электронов равной
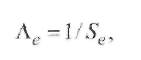 (2.22) (2.22)
что отвечает минимуму соответствующей данному газу кривой Рамзауэра.
В приэлектродных областях дуги температуры электронов Те и газа Тане равны, термическое равновесие не соблюдается (Те ≠ Та) и электроны могут набирать энергию до 8...20 эВ. На рис. 2.9 это примерно соответствует газокинетическим сечениям молекул.
Средний газокинетический пробег иона Λ־i в слабых полях мало отличается от пробега молекул, т. е. для ионов (если диаметры иона и молекулы считать равными) имеет место соотношение
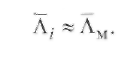 (2.23) (2.23)
Скорость электронов намного больше скорости молекул ve » vм. Кроме того, согласно кинетической теории газов электрон можно считать точкой (de « du). Это значит, что электрон может подойти к центру молекулы на расстояние dм/2, поэтому площадь круга эффективного соударения Qea будет вчетверо меньше. Учитывая это, получим газокинетический пробег электрона
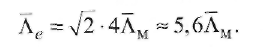 (2.24) (2.24)
Например, в воздухе при Т = 300 К и атмосферном давлении для газов Λ־м = 1 • 10 -7 м. В плазме при Т = 6000 К значение Λ־м будет в 20 раз больше (см. формулу (2.9)), а Λ־е ≈ 20 • 5,6 • 10-7 ≈ 1,1 • 10-5 м. Такое значение (Λ־е ≈ 10-5 м) часто принимают при расчете в приэлектродных областях дуги наряду с Λ־i ≈ 10-7 м. Вычисленный по Рамзауэру пробег электрона в плазме Λе может отличаться от газокинетического Λ־е в десятки раз.
2.2.6. Упругие и неупругие соударения
Электрическое поле дуги напряженностью Е сообщает за 1 с энергию jE электронам и ионам в 13 м столба. Электроны воспринимают наибольшую часть этой энергии и в результате соударений передают ее атомам и ионам. Возможны два вида соударений - упругие и неупругие:
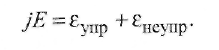 (2.25) (2.25)
Электрон, который близко подходит к атому, отталкивается электронным облаком атома и нарушает, в свою очередь, расположение облака. Окончательный результат зависит от скорости электрона (его энергии и направления движения). Медленный электрон легко отражается, а электронное облако атома претерпевает лишь незначительное возмущение; это так называемое упругое соударение. С позиций классической физики его можно представить как столкновение двух идеально упругих шаров, обменивающихся кинетической энергией. Изменения потенциальной энергии атома здесь не происходит.
При неупругих соударениях частиц энергия передается в виде энергии диссоциации εд, возбуждения εв или ионизации εi, причем за одно столкновение может быть передана энергия порядка нескольких электронвольт. При этом электрон нейтрального атома переходит с низкого энергетического уровня на более высокий, потенциальная энергия атома увеличивается и атом возбуждается либо ионизируется.
Энергия диссоциации εд молекул различных газов имеет следующие значения:
Газ Н2 02 N2 F2 C02
εд,эВ 4,48 5,08 7,37 1,6 9,7
Запасенная в возбужденных атомах энергия уходит из них в виде излучения - столб дуги светится.
2.2.7. Потенциал ионизации
Ионизацию можно рассматривать как крайний случай возбуждения, когда электрону сообщается энергия большая, чем энергия самого высокого возбужденного уровня атома.
Чтобы вырвать электрон из атома (молекулы), нужно затратить энергию, равную энергии его связи в атоме. Эту энергию называют потенциалом ионизации Ui,- и часто выражают в вольтах (точнее, в электронвольтах). Первый потенциал ионизации - потенциал ионизации, соответствующий удалению наиболее слабо связанного электрона из нейтрального невозбужденного атома; удалению из ионизованного атома следующих электронов соответствуют второй, третий и т. д. потенциалы ионизации.
Значения первого потенциала ионизации Ui атомов некоторых элементов приведены ниже:
Атом Cs К Na Ca Fe Н О N Аг F Ne Не
Ui, эВ 3,9 4,3 5,11 6,08 7,83 13,53 13,56 14,5 15,6 18,6 21,5 24,6
2.2.8. Термическая ионизация
Неупругие соударения частиц между собой при высоких температуре и плотности газа приводят к так называемой термической ионизации, которая возникает за счет кинетической энергии частиц. Наиболее вероятна следующая схема неупругого соударения быстрого электрона и атома:
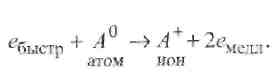
Результатом неупругого соударения будет образование иона и двух электронов, обладающих малыми скоростями. Затем электроны снова начнут ускоряться электрическим полем.
Ионизация холодной плазмы осуществляется весьма небольшим числом высокоскоростных электронов, соответствующих «хвосту» максвелловского распределения. Поэтому неупругих столкновений в сварочном столбе дуги обычно значительно меньше, чем упругих.
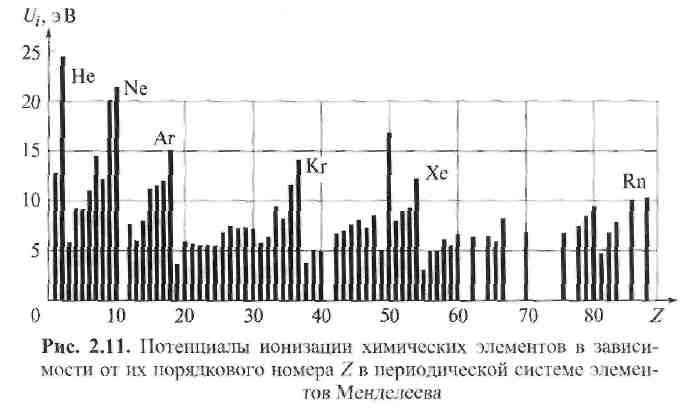
Энергия ионизации, численно равная Ui зависит от строения атома, т. е. от его места в периодической системе элементов Менделеева (рис. 2.11). Потенциал ионизации Ui представляет собой периодическую функцию атомного номера элемента Z, и значения Ui снижаются с уменьшением номера группы и увеличением номера периода таблицы Менделеева. Наименьший потенциал ионизации (Ui = 3,9 эВ) имеют пары цезия Cs. Единственный валентный электрон у щелочных металлов первой группы слабо связан с ядром, поэтому и энергия ионизации щелочных металлов невелика. Наивысший потенциал Ui =24,6 эВ наблюдается у самого легкого из инертных газов - гелия Не. Оболочка инертных газов заполнена и поэтому наиболее прочна.
|
|
|
 Скачать 4.1 Mb.
Скачать 4.1 Mb.