ТСП 11. I источники энергии для сварки глава физические основы и классификация сварочных процессов
 Скачать 4.1 Mb. Скачать 4.1 Mb.
|
|
Фотоионизация Атомы и молекулы могут возбуждаться не только при соударениях между собой или с ионами и электронами, но и путем поглощения квантов излучения, которые появляются в столбе дуги при рекомбинации других сильно возбужденных атомов. Условие фотоионизации выражается формулой где h = 4,13∙10-15 эВ∙с - постоянная Планка; v = c/λi – частота колебаний; с - скорость света; λi - длина волны электромагнитного излучения, способного вызвать ионизацию атомов, м. Из условия (2.27) получаем выражение для λi 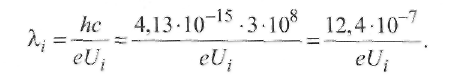 (2.28) (2.28)Чем больше потенциал ионизации элементаUi, тем меньше требуемая длина волны λi. Для сварочной дуги значения eUi составляют 4...25 эВ и соответствующие длины волн находятся в ультрафиолетовой части спектра. Например, для аргона eUi= 15,7 эВ, λi = 1,24-10-6 /15,7 = 7,85∙10-2 мкм, а для щелочных металлов eUi= 4...6 эВ; λi= 0,2...0,3 мкм. Фотоионизация в плотной плазме, видимо, незначительна по сравнению с термической ионизацией, причем выделить их доли расчетным и опытным путем пока не удается. 2.2.10. Деионизация В любой точке стационарного разряда концентрация заряженных частиц любого типа определяется равенством скоростей образования и потерь частиц в этой точке. Ионизация в плазме приводит к разделению зарядов, но электрическое притяжение ограничивает степень возможного разделения и плазма остается квазинейтральной. Наряду с ионизацией непрерывно происходят уравновешивающие ее процессы деионизации. К ним относятся рекомбинация заряженных частиц в нейтральные, захват электронов (прилипание), дрейф проводимости и диффузионные процессы, выравнивающие концентрацию (амбиполярная диффузия). Скорость рекомбинации ионов и электронов в нейтральные частицы при их концентрациях ni, nе, па определяется коэффициентом рекомбинации R по уравнению Коэффициент рекомбинации R тем больше, чем больше плотность частиц. Он зависит также от сорта частиц, времени их жизни, от размеров ионов, от наличия близко расположенных тел (нейтральных атомов воздуха или охлаждающих стенок). Проводимость газового разрядного промежутка определяют прежде всего электроны как высокоскоростные частицы. Захват электронов атомами (прилипание) и ионами в процессе рекомбинации можно в некоторых случаях рассматривать как обратимый процесс, а в других - как практически необратимый процесс. Например, процесс Na+ + e ↔ Na0 можно считать обратимым. Если же при сварке в состав покрытия электрода или флюса вводят плавиковый шпат CaF2, то в этом случае может происходить необратимый захват электрона фтором. Захват электронов с образованием тяжелых отрицательных ионов может осуществляться и другими атомами металлоидов, которые обладают довольно большим сродством к электрону (3.. .4 эВ). В дуговом разряде под флюсом из галогенов могут происходить, например, такие процессы: F + е → F-1 + 3,94 эВ; О + е → О-1 + 3,8 эВ; С1 + е → Сl-1 + 3,7 эВ; Н + е → Н-1 + 0,76 эВ. Порядок значения сродства к электрону таков, что указанные процессы могут считаться обратимыми. Но быстрая рекомбинация образовавшихся отрицательных ионов и положительных ионов металлов в молекулы (R велико) приводит к более интенсивной деионизации разрядного промежутка.
Я 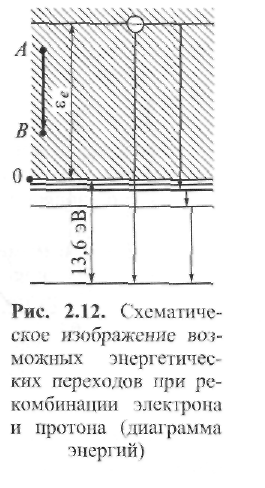 вление рекомбинации электрона и иона заключается в том, что свободный электрон, пролетая в поле иона, захватывается им и переходит в связанное состояние. При этом освобождается энергия, равная сумме кинетической энергии свободного электрона и его энергии связи. Например, если электрон с энергией ее захватывается протоном и в результате образуется нормальный атом водорода, то полный выигрыш энергии составит εе + 13,6 эВ (рис. 2.12). вление рекомбинации электрона и иона заключается в том, что свободный электрон, пролетая в поле иона, захватывается им и переходит в связанное состояние. При этом освобождается энергия, равная сумме кинетической энергии свободного электрона и его энергии связи. Например, если электрон с энергией ее захватывается протоном и в результате образуется нормальный атом водорода, то полный выигрыш энергии составит εе + 13,6 эВ (рис. 2.12).Заштрихованная область на диаграмме энергий соответствует свободным электронам. Их кинетическая энергия отсчитывается от линии нулевого уровня вверх. Нормальное состояние электрона, связанного в атоме водорода, соответствует отрицательной энергии 13,6 эВ. Напомним, что за нулевой уровень энергии условно принимается состояние, при котором связь между ядром и электроном разорвана и эти частицы разведены на очень большое расстояние с нулевой кинетической энергией. Освобождающаяся энергия может излучаться в виде фотона с энергией εе + 13,6 эВ. Возможен также ступенчатый переход, при котором атом сначала оказывается в одном из доступных возбужденных состояний, а затем перескакивает на нормальный уровень. Это изображено на правой стороне диаграммы. Тормозному излучению соответствует изменение энергетического состояния электрона в заштрихованной области (переход между точками А и В). Так как свободные электроны обладают непрерывным набором энергий, то фотоны, излучаемые в процессе рекомбинации, образуют сплошной спектр, на который накладывается линейчатый спектр возбужденных атомов, образующихся при ступенчатых переходах. Для сварочных дуг, имеющих Те ≈ Тi ≤104 К, излучение рекомбинации преобладает над тормозным излучением электронов и имеется преимущественно сплошной спектр с максимумом длин волн излучения в видимой и ультрафиолетовой областях оптического диапазона 0,3... 1,0 мкм. Спектр сварочной дуги в парах металлов приближается к спектру солнечного излучения с небольшим сдвигом в сторону длинных волн (рис. 2.13). Сплошной спектр интегрально дает наибольшую часть излучения дуги. Однако интенсивность отдельных линий линейчатого спектра на фоне сплошного спектра значительно выше. По частоте (длине волны) и интенсивности определенных спектральных линий, излучаемых в разных зонах дугового разряда, можно судить о концентрации возбужденных атомов и, следовательно, о температуре зоны. Сравнивая интенсивности спектральных линий, делают заключение об электронной температуре плазмы и степени приближения ее к термодинамическому равновесию. Важные сведения о плотности электронов в плазме получают, измеряя уширение спектральных линий. 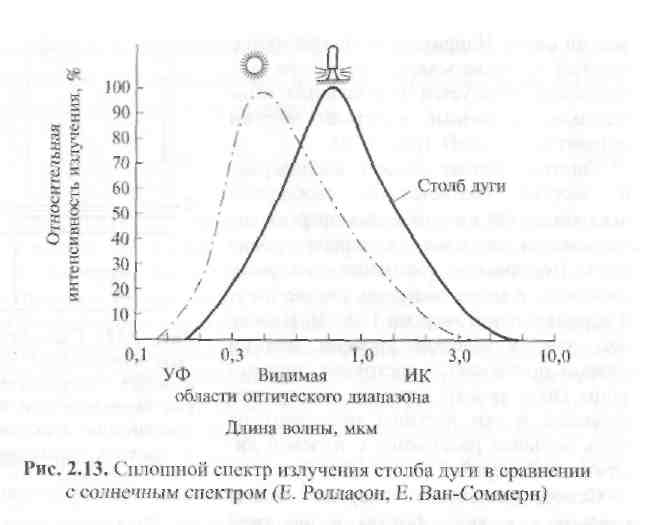
Направленное движение ионов и электронов в плазме может быть вызвано двумя причинами: электрическим полем, создающим ток, или же разницей в концентрации частиц между различными участками плазмы. Кроме того, в неравномерно нагретой плазме обмен частицами между областями с различной температурой создает механизм плазменной теплопроводности, благодаря которому через плазму идет поток тепловой энергии. Перечисленные процессы объединяются общим названием - явление переноса. Они обеспечивают переход от неравновесного к равновесному состоянию. 2.3.1. Электропроводность Важнейшим свойством плазмы является способность переносить заряженные частицы под действием электрического поля. При наложении электрического поля возникают силы, заставляющие электроны дрейфовать - двигаться вдоль силовых линий поля; на хаотическое тепловое движение электронов накладывается их упорядоченное движение со скоростью дрейфа. Пользуясь законами классической физики, можно оценить ее порядок по сравнению со скоростью теплового движения. Электрический ток создается направленным потоком электронов. В простейшем случае при неизменной силе тока имеет место равновесие между силой, с которой действует на электроны электрическое поле, и силой торможения, обусловленной столкновениями между электронами и ионами. Сила торможения равна среднему значению импульса, теряемого электроном при столкновении с ионами. Полагаем, что движение электрона как частицы с массой mе и зарядом е под действием поля напряженностью ¯Е и ускоряющей силы е¯Е происходит в течение времени τе = Λ / ve, где ve - средняя квадратичная скорость электрона (скорость теплового движения, так как скоростью дрейфа пренебрегаем вследствие ее сравнительной малости), а Λ - средняя длина свободного пробега электрона. При движении с ускорением е¯ Е/meза время τе электрон разгоняется до скорости дрейфа (2.30) Плотность тока у в плазме равна сумме электрических зарядов, пересекающих единичную площадку за 1 с: (2.31) Подставляя в (2.31) значение ve из (2.30), получаем выражение закона Ома для плазмы Здесь σ - удельная электропроводность плазмы (См/м, Ом-1 • м-1 ): Величину называют подвижностью носителя тока (электрона), а уравнение (2.34) известно как уравнение Ланжевена. Входящая в уравнение (2.34) величина τе характеризует среднее время пробега электронов по отношению к столкновениям, в результате которых тормозится электронный поток, поэтому средняя частота столкновений электрона Столкновения электронов между собой не учитываются, так как они не приводят к торможению электронного потока. При изучении представляют интерес два крайних случая электропроводности плазмы: а) полностью ионизованная плазма при степени ионизации χ ≈ 1, па ≈ 0; б) слабо ионизованная плазма при χ ‹‹ 1, na≈ ni≈ ne(при однозарядных ионах). Удельная электропроводность полностью ионизованной плазмы, состоящей из однозарядных ионов, определяется по Л. Спитцеру (Qea = 0, τе= τеi , пе = niz, z - заряд ионов): 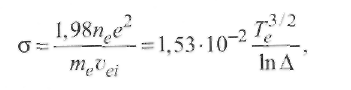 (2.36) (2.36)Где Δ= 1,24 ∙ 107(Tе3/nе)1/2 (кулоновский логарифм ln Δ = 4...11). Оказывается, что в этом случае удельная электропроводность σ почти не зависит от концентрации электронов пе, так как с ростом пе уменьшается время пробега τеi. При одной и той же температуре σ тем больше, чем меньше заряд ионов z; σ растет пропорционально Те3/2, т. е. весьма быстро. Например, при Те = 15 • 106К водородная плазма имеет такую же удельную электропроводность, как обыкновенная медь при комнатной температуре: σ ≈ 6 ∙ 107См/м. Д 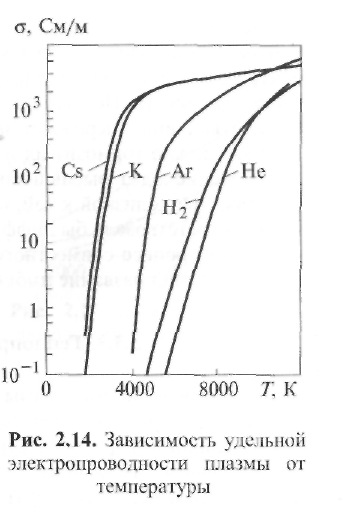 ля слабоионизованной плазмы торможение электронов происходит главным образом вследствие столкновений с нейтральными атомами и молекулами. ля слабоионизованной плазмы торможение электронов происходит главным образом вследствие столкновений с нейтральными атомами и молекулами.В этих случаях Qei мало, тогда τе = Δ/v = τеa = 1/(nav¯Qea). Найдем удельную электропроводность согласно уравнению (2.33): Черта над произведением ¯vQea¯ означает, что берется среднее значение этого произведения с учетом распределения электронов по скоростям и зависимости Qea от ve. Из формулы (2.37) видно, что удельная электропроводность слабо ионизованной плазмы пропорциональна степени ионизации ne /na. Поэтому σ должна быть мала вследствие недостатка в носителях тока. Она в десятки тысяч раз меньше электропроводности меди. Удельная электропроводность слабоионизованной плазмы с ростом температуры газа быстро нарастает на участке, соответствующем росту концентрации электронов (рис. 2.14). 2.3.2. Амбиполярная диффузия Направленные потоки ионов и электронов в плазме могут возникать не только под действием электрического поля, но и в условиях, когда концентрация частиц в различных точках неодинакова. В этих случаях силой, приводящей в движение частицы, будет разность давлений. В слабо ионизованной плазме давление электронной и ионной составляющих мало по сравнению с давлением нейтрального газа, поэтому при диффузионном движении заряженных частиц так же, как и при прохождении тока, происходит не перемещение всей массы вещества, а только перемещение составляющих. Характерной особенностью процесса является то, что по условию квазинейтральности скорости диффузии электронов и ионов должны быть одинаковы. Поскольку электроны обладают большой подвижностью, они опережают ионы, создавая электрическое поле, которое сильно тормозит их и слегка ускоряет тяжелые частицы -ионы. Происходит выравнивание скоростей, и весь процесс идет со скоростью, близкой к той, которая в отсутствие электрического поля соответствовала бы диффузионному движению ионов. Такой процесс совместного движения ионов и электронов через газ получил название амбиполярной диффузии. 2.3.3. Теплопроводность плазмы Теплопроводность плазмы также обусловлена движением частиц. Главную роль в переносе теплоты от горячих участков плазмы к холодным играют электроны (благодаря их большей скорости теплового движения). Если вдоль некоторого направления существует перепад температур, то электроны с большими энергиями идут в одну сторону, а с меньшими - в другую. В результате появляется поток тепловой энергии qT в сторону более холодных слоев плазмы, прямо пропорциональный относительному перепаду температур, т. е. температурному градиенту: Здесь λ - коэффициент теплопроводности, называемый далее для краткости теплопроводностью. Для плазмы имеет место соотношение λ = λ а+ λ е, т. е. учитываются атомный (λ а) и электронный (λ е)механизмы теплопередачи, причем 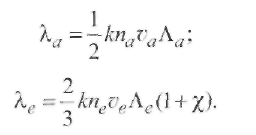 (2.39) (2.40) (2.39) (2.40)В 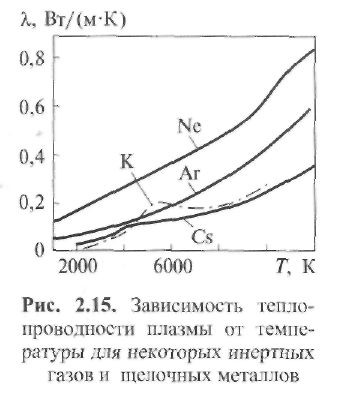 центре столба дуги из-за больших значений Λе и ve справедливо неравенство χе » χа, а на границах столба значение χе мало вследствие малости пе. центре столба дуги из-за больших значений Λе и ve справедливо неравенство χе » χа, а на границах столба значение χе мало вследствие малости пе.Подставляя в уравнение (2.39) k = 1,38∙10-23 Дж∙К-1 , выражения для Λ (см. (2.16)) и скорости теплового движения (2.41) (А - атомная масса, а T- температура газа, К), получаем 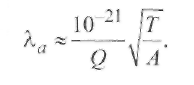 (2.42) (2.42)Для инертных газов Ar, Ne теплопроводность в интервале температур 7000... 12 000 К изменяется плавно, увеличиваясь с ростом температуры (рис. 2.15). Для легко ионизируемых щелочных металлов (цезия и калия) коэффициент теплопроводности имеет характерный максимум, который, по-видимому, обусловлен механизмом ионизации. 2.4. Элементы термодинамики плазмы 2.4.1. Термическое равновесие Термическое равновесие в дуговом промежутке будет полным, если частота появления всех возможных энергетических состояний удовлетворяет распределению Максвелла - Больцмана. В плотной среде столба дуги столкновения между частицами приводят к быстрому установлению локального равновесного состояния. Напротив, в разреженной плазме, где столкновения частиц происходят редко, могут длительное время существовать неравновесные состояния. Понятие термодинамической равновесности предполагает, что состояние вещества полностью определяется его химическим составом и какими-либо двумя термодинамическими параметрами. Одним из них всегда служит температура Т, общая в данном случае для электронов и тяжелых частиц. Другим может быть плотность или давление. Обычно это именно давление, ибо даже в условиях, когда плазма участвует в каких-то движениях, движения эти происходят медленно по сравнению со скоростью звука и давление, следовательно, быстро выравнивается в пространстве. Плотность плазмы при этом в каждом месте «автоматически подстраивается» к температуре. Наибольший интерес представляют дуговые разряды, существующие при атмосферном давлении, в частности сварочные дуги. В случае равновесной плазмы нет необходимости вникать в сложную кинетику ионизации газа и гибели электронов; температура и давление однозначно определяют степень ионизации и электрические или электромагнитные характеристики плазмы. И сам процесс ионизации отличен от того, что происходит в слабоионизованной неравновесной плазме, в которой молекулы ионизуются электронами, непосредственно ускоренными внешним полем до потенциала ионизации. В случае равновесной плазмы действие поля как бы «обезличивается», тюле является поставщиком энергии для электронного газа в целом. Термическая ионизация происходит совершенно независимо от того, каким путем в газ поступает энергия. Рассмотрим кратко границы применения термодинамических характеристик в плазме сварочной дуги. Покажем, например, что в дуге существует локальное термическое равновесие, которое устанавливается достаточно быстро. Электроны при плотности тока j от электрического поля Е получают в 1 м3 за 1 с энергию где be = ve/E - подвижность электрона; ve = еЕr/m - дрейфовая скорость электрона (см. (2.30)). Для определения полного числа условных столкновений, испытываемых электроном за 1 с, надо сложить частоты vвсех видов столкновений: с ионами (vei = 1/τеi), с атомами (vеа = 1/τеa) и электронами (vee = 1/τеe): Однако для плотной плазмы важно наличие тяжелых частиц (ионов, атомов), при столкновении с которыми вектор скорости электронов претерпевает хаотическое (в среднем равномерное) рассеяние. При этом становится возможным превращение кинетической энергии электронов в энергию беспорядочного теплового движения других частиц. Полная нерегулярность направлений скорости электронов достигается уже после небольшого числа столкновений. Формула для времени пробега τеa имеет вид 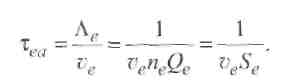 Положим nе = 1024м-3 и vе = 108м/с. Сечение Рамзауэра для столкновении электронов с тяжелыми частицами Qe = 10-20м2 (см. рис. 2.9), a Se = neQe= 1024∙10-20 = 104 м-1. Тогда для плазмы дуги в аргоне получим время пробега τеa=1/(108∙ 104) ≈ 10-12с, (2.46) т. е. время установления равновесия мало. При каждом столкновении электрон отдает свою избыточную (но не полную) энергию, полученную от поля напряженностью Е, прямо пропорционально отношению 2me/ma. Таким образом, для выравнивания температуры газа и электронов необходимо число ma/(2me) = 103 ...105 соударений (здесь 103 примерно соответствует отношению масс в водородной плазме, где ma≈ 1840 mе, а 105 относится к аргоновой или ртутной плазме). В то же время электроны непрерывно получают энергию от поля. Поэтому устанавливается электронная температура Те, которая превышает температуру дуги Tд на величину ΔT. Энергия jE, полученная электронами от поля (см. (2.43)), должна быть равна энергии, отдаваемой электронами частицам газа при столкновениях в 13 см за 1 с вследствие разности температур ΔT ≈ Те-Tд, т. е. С учетом того, что частота соударений в секунду v = 1/ τ (τ = Δ/v), а при максвелловском распределении электронов по скоростям в плазме их средняя квадратичная скорость v = √3kTe/me(см. разд. 2.1), получим, разделив обе части (2.47) на 3/4kTe : 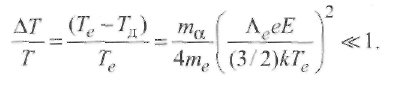 (2.48) Здесь Т - температура равновесной (термической) плазмы; ΛееЕ -энергия Δε, получаемая электроном от поля на участке пробега Λ е, а (3/2)кТе - энергия ε теплового движения электрона. Для термического равновесия необходимо, чтобы Δ εе/ε и относительная разность температур ΔT/T были значительно меньше единицы. Учитывая формулу (2.18), получаем т. е. Δε определяется в основном отношением Е/р. Из формул (2.48) и (2.49) следует, что термическое равновесие легче достигается при малой напряженности поля Е, повышенном давлении р(малый пробег Λе) и высокой температуре газа дуги Tд. |
