ТСП 11. I источники энергии для сварки глава физические основы и классификация сварочных процессов
 Скачать 4.1 Mb. Скачать 4.1 Mb.
|
|
Пример 2.2. Определить, существует ли термическое равновесие в столбе дуги при сварке вольфрамовым электродом. Решение. Приняв для W-дуги в аргоне р = 105 Па, Qea= 2,5 ∙ 10-20 м2 , Е = = 1 ∙ 103 В/м, Λеа = 3 ∙ 10 -6 м, mAr = 105, кТ ≈ 2 эВ, т. е. около 23 000 К, получим: 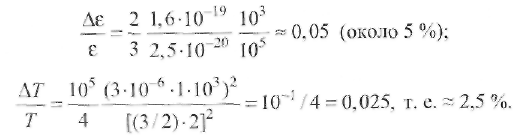 Отсюда делаем вывод: термическое равновесие в столбе дуги существует, так как Пример 2.3. Определить, существует ли термическое равновесие в плазме вакуумной дуги при давлении р = 0,1 Па в парах железа: QFeea = 50 ∙ 10-20 м2 и E=50 В/м.. Решение. Расчет по формуле (2.49) дает т. е. энергия, получаемая электронами от поля, здесь значительно больше, чем энергия их теплового движения, что должно привести к росту электронной температуры. Действительно, принимая ma/me = 104 и учитывая выражение (2.18) для Λ е при T ≈ 5800 К и кТ = 1,38 ∙ 10-23 ∙ 5800 = 0,8 • 10-19 Дж, получаем: при p= 105 Па т. е. пробег мал по сравнению с длиной дуги; при р = 0,1 Па пробег Λ е увеличивается (при Т= const) в 106 раз и составляет 1,6 м, т. е. пробег больше длины дуги. Приняв условно Те ≈ 0,8 • 105 К, кТ ≈ 7 эВ, получим по формуле (2.51): Т 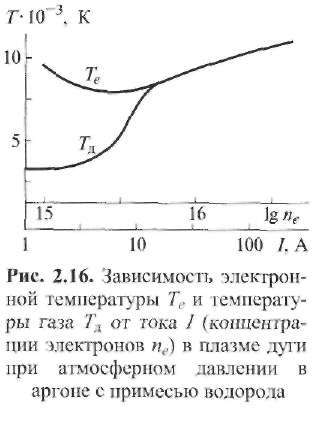 аким образом, в вакуумной дуге термического равновесия нет и электронная температура Те может значительно превышать температуру тяжелых частиц Tд. аким образом, в вакуумной дуге термического равновесия нет и электронная температура Те может значительно превышать температуру тяжелых частиц Tд.В дугах низкого давления, а также в приэлектродных областях дуги, где напряженность поля Е велика и, следовательно, отношение Е/р велико, энергия Δε, получаемая электронами от поля, растет и термическое равновесие нарушается. Плазма воздуха и других молекулярных газов, а также паров металлов при атмосферном давлении и токах более 10А является равновесной. Это обусловлено интенсивным обменом энергией между электронами и молекулами через возбуждение колебаний и вращений, а в парах металла - большими сечениями упругого рассеяния электронов. В инертных газах разность температур Те - Тд больше вследствие относительной малости сечений рассеяния электронов атомами (см. рис. 2.9). Так, в аргоне при атмосферном давлении (рис. 2.16) электронная и газовая температуры совпадают (Те ≈ Тд ≈ 8000 К) только при I >10 А, когда пе 3 ∙ 1015 см-3 . Еще хуже устанавливается равновесие в гелии, где только при I ≈ 200 А, когда пе ≈ 5 • 1016 см-3 , температуры выравниваются: Те ≈ Tд ≈ 10 000 К. 2.4.2. Уравнение Саха Плазму столба сварочной дуги при атмосферном давлении можно отнести к категории термической плазмы, свойства которой определяются температурой и давлением. В отличие от изотермической плазмы, в которой grad T = О, в термической плазме столба дуги температура меняется от точки к точке, но в каждой точке сохраняется локальное термодинамическое равновесие с одной и той же равновесной температурой для всех частиц и процессов. Считается, что, хотя весь объем плазмы в целом и не находится в равновесии, его отдельные макроскопически малые части приходят в состояние равновесия, так что можно говорить о локальном равновесии в небольших частях рассматриваемой плазменной системы. Важнейшей характеристикой плазмы является ее состав. Расчет состава плазмы, находящейся в состоянии термодинамического равновесия, основан на законе действующих масс. Равновесный состав плазмы не зависит от того, как происходят реакции, а зависит только от условий, в которых она находится. Поэтому при выводе условия равновесия можно предполагать, что реакции происходят при заданных постоянных температуре Т и объеме V. Приведем простейшие примеры применения закона действующих масс. Можно рассматривать термическую ионизацию как обратимую химическую реакцию газов Напомним, что степень ионизации - это отношение числа заряженных частиц (ионов или электронов) в плазме к числу всех частиц: χ = пе /(па + пе) = пi /(па + пi) Степень ионизации χ определяется из константы равновесия реакции с помощью уравнения Саха, которое справедливо при малой степени ионизации χ ‹‹ 1 Если входящие в уравнение Саха величины выражены в единицах СИ, то оно имеет вид где ge gi ga - статистические веса квантовых состояний соответственно электрона, иона и атома; Ui- потенциал ионизации, В. Для электрона ge = 2, что соответствует двум направлениям спина. Для ионов и нейтральных атомов значения gi и ga вычисляют, учитывая строение атомов. Концентрацию электронов определяют по формуле 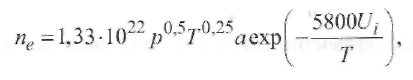 (2.51) (2.51)где a = ge gi /ga = 2gi / ga - квантовый коэффициент. Значения а2 , вычисленные К.К. Хреновым для различных химических элементов, находятся в диапазоне 1...4: для атомов с регулярным строением оболочки Группы таблицы Менделеева I III III V V VI VII VIII а2 1 4 1 4/3 3/2 8/3 3 4 для атомов с нерегулярным строением оболочки Элементы N С Cr Mn Fe Cu Nb La W Th a2 8/5 3 8/7 7/3 12/5 3 1 1 8/5 4/3 Кривые зависимости степени ионизации от температуры, построенные по уравнению Саха, имеют S-образный вид (рис. 2.17). Например, при атмосферном давлении для калия (Ui = 4,3 В) χ ≈ 1 при 11 000 К; для водорода (Ui =13,5 В) χ ≈ 1 при 24 000 К; для гелия (Ui = 24,5 В) χ ≈ 1 при 50 000 К. Надо иметь в виду, что уравнение Саха дает результаты, близкие к экспериментальным, только при малых степенях ионизации (χ << 1). При 6000 К расчет по уравнению (2.50) для Na дает χ ≈ 0,21; для Аг получаем χ ≈ 0,23 • 10-4 . Следовательно, степень ионизации Аг по сравнению с Na меньше в 104 раз. 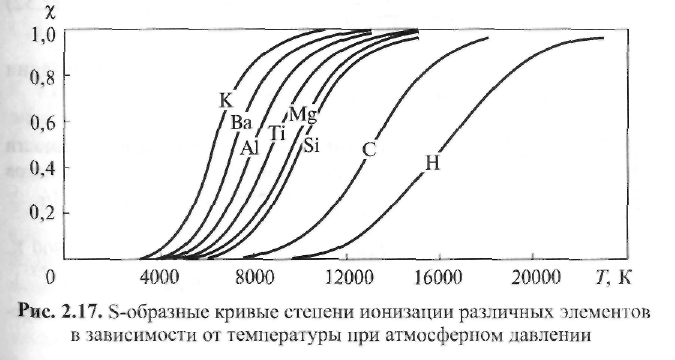 2.4.3. Эффективный потенциал ионизации Так как дуговой разряд существует обычно не в однородном газе, а в смеси газов и паров, находящихся при высокой температуре, то необходимо знать эффективный потенциал ионизации Uэф. Практика показывает, что в смеси газов в большей степени ионизируется газ с наименьшим потенциалом ионизации Ui. Расчет эффективного потенциала Uэф термической ионизации смеси был выполнен В.В. Фроловым. Под эффективным потенциалом ионизации Uэф смеси газов, обладающей степенью ионизации χэф следует понимать потенциал ионизации некоторого однородного газа, в котором (при температуре и общем давлении смеси) число заряженных частиц такое же, как и в газовой смеси: 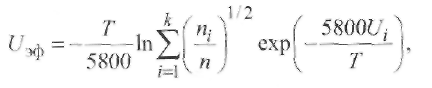 (2.52) (2.52)где ni - концентрация i-го газа в смеси; Ui - потенциал ионизации i-го газа в смеси k газов; T- температура, К. П 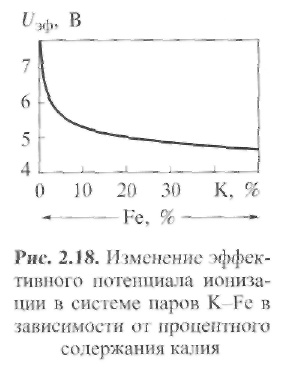 ример 2.4. Рассчитать Uэф в зависимости от концентрации газовой смеси из паров калия и железа: Uk = 4,32 В; U Fe = 7,83 В. ример 2.4. Рассчитать Uэф в зависимости от концентрации газовой смеси из паров калия и железа: Uk = 4,32 В; U Fe = 7,83 В.Решение. Предположим, что Т - 5800 К. Тогда UFe = -1 • ln(nK1/2e-4,32 + nFe 1/2e-7,83). Результаты расчета приведены в виде графика на рис. 2.18. С понижением температуры плазмы еще больше возрастает влияние компонента с наиболее низким потенциалом ионизации Ui на общее значение Uэф. Следовательно, сравнительно небольших добавок ионизаторов достаточно для обеспечения стабильности горения дуги при сварке под флюсом или штучными электродами с покрытием. 2.5. Баланс энергии и температура в столбе дуги 2.5.1. Баланс энергии в столбе дуги Пренебрегая очень небольшой долей энергии, получаемой ионами при их ускорении в продольном поле (ионный ток мал), можно считать, что вся энергия, отбираемая дуговым разрядом от внешнего источника, в столбе дуги переходит непосредственно к электронам плазмы. Эта энергия расходуется на возбуждение и ионизацию молекул газа, а также на повышение их кинетической энергии при упругих столкновениях. Баланс мощности для единицы длины столба дуги имеет вид где РИ, РT и РK - потери мощности столба дуги соответственно излучением, теплопроводностью и конвекцией. Отношение PИ/(PT + РК) зависит от параметров режима дуги (I, U, lд), формы столба дуги и рода атмосферы (газовой среды). Для слаботочных дуг, ограниченных стенками, В. Эленбаас и Г. Геллер пренебрегли величинами РИ, РK и рассчитали баланс энергии. При этом столб дуги рассматривался как цилиндрический сплошной токопроводящий стержень с удельной электрической проводимостью σ, в котором вся подводимая к единице объема электрическая энергия (джоулева теплота) jE = σЕ2 отводится за счет теплопроводности на охлаждаемые стенки разрядной трубки радиусом R. Подобные условия часто встречаются при практическом использовании различного вида сварочной дуги. Даже если дуга горит в свободной атмосфере или обдувается потоком газа, такая модель дает представление о состоянии в токопроводящем канале, поскольку температура на оси дугового разряда не очень чувствительна к внешним условиям. Так, при атмосферном давлении в дуговом разряде (I = 20... 100 А) температура аргоновой плазмы не превышает 11 000... 12 000 К. Потери на излучение в большинстве случаев заметно уступают выносу энергии из столба дуги за счет теплопроводности, поэтому ими можно пренебречь. Баланс энергии плазмы описывается уравнением теплопроводности с энерговыделением в виде джоулевой теплоты (уравнение Эленбааса - Геллера): 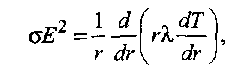 (2.54) (2.54)где λ - теплопроводность. Закон Ома для равновесной плазмы выражается формулой Запишем граничные условия к уравнениям (2.54), (2.55): при r= R температура Т = Тс, где Тс - температура стенки; при r = О производная dT/dr= 0 вследствие симметрии. Температура токопроводящей плазмы гораздо выше температуры стенки, так что, по существу, можно положить Тс = 0. Ток дуги равен 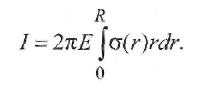 (2.56) (2.56)Сложность решения уравнения (2.54) заключается в нелинейной зависимости (σ (Т) и λ (Т)) свойств плазмы от температуры. Далеко не всегда функции σ(Т) и λ(T) могут быть представлены в виде зависимости, допускающей аналитическое решение уравнений (2.54), (2.55). Нелинейность уравнения (2.54), связанная с функцией λ(Т), устраняется известным в теплофизике приемом введения вместо температуры плазмы Т тепловой функции (теплового потенциала) 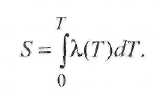 (2.57) (2.57)П 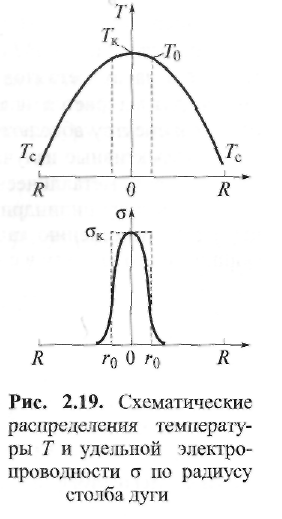 осле формальной замены температуры Т на функцию S уравнение (2.54) принимает вид осле формальной замены температуры Т на функцию S уравнение (2.54) принимает вид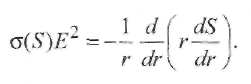 (2.58) (2.58)Для выбранного газа тепловая функция S однозначно связана с температурой плазмы соотношением (2.57). Каналовая модель. Предположим, что температура Тк и удельная электропроводность σк постоянны в поперечном сечении дуги внутри токопроводящего канала эффективного радиуса r0 и при r ≤ r0 имеет значения: Tк = T0, σ к = σ0 Тогда дуга представлена двумя областями: проводящей при 0 ≤ r ≤ r0 и непроводящей (σ = 0) при r0 ≤ r ≤ R. Каналовая модель сводится к замене истинной зависимости σ(r) ступенчатой, показанной на рис. 2.19 штриховой линией. В этом приближении выражение (2.56) для тока дуги приобретает вид а уравнение (2.58) в непроводящей области легко интегрируется. В проводящей области в соответствии с принятыми допущениями тепловой потенциал S1 – S0 постоянен. Используя граничные условия S1 (r0) = So = S2(r0) и S2(R) = 0, решение уравнения (2.58) в непроводящей зоне можно привести к виду 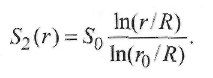 (2.60) (2.60)Отсюда найдем тепловой поток q на стенку трубки и равное ему выделение мощности Р в единице длины столба дуги: 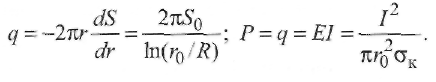 (2.61) (2.61)Уравнения (2.57), (2.59) и (2.61) содержат три неизвестные величины: температуру на оси дуги, эффективный радиус электропроводящего канала r0 и напряженность электрического поля Е (ток I и радиус канала R являются задаваемыми параметрами). Для получения недостающего соотношения М. Штеенбек предложил использовать принцип минимума мощности. При заданных I и R в трубке должны установиться (в рамках каналовой модели) такие температура плазмы T0 и эффективный радиус канала гr0, чтобы мощность Р и Е = P /Iоказались минимальными. Известно, что для дуг в парах металлов при I= 100... 1000 А до 90 % энергии столба дуги теряется излучением. Спектр излучения таких дуг близок к спектру абсолютно черного тела, т. е. они представляют собой эффективные излучатели. Для краткости будем далее такие дуги называть металлическими или Ме-дугами. Считая дугу цилиндрической по форме с постоянной плотностью тока по сечению канала, К.К. Хренов (1949) принял баланс мощности столба дуги в следующем виде (каналовая модель дуги): где σ иT4 - удельное излучение по закону Стефана - Больцмана. Пример 2.5. Сравнить потери излучением (Ри) и теплопроводностью (Рт) столба «железной» дуги при T = 5000 К, если QFe = 50 • 10-20 м ; ΔT/ Δ х = = 107 К/м; АFe = 54; σ и = 5,7 • 10 -8 Вт/(м2 • К4). Решение. Используя формулы (2.62) и (2.42), получаем 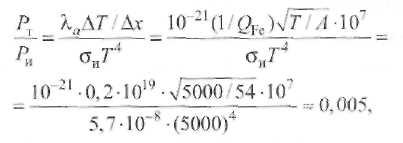 что подтверждает приемлемость каналовой модели. 2.5.2. Температура дуги Применяя далее уравнение (2.31) и определяя концентрацию электронов как пе = χ п с помощью уравнений Саха (2.50), (2.51), а также используя принцип минимума мощности Штеенбека, К.К. Хренов получил выражение для температуры в столбе дуги: (2-63) где Uэф - эффективный потенциал ионизации в плазме. Опыт показал, что уравнение (2.63) справедливо для ручной дуговой сварки штучными электродами с покрытием, а для сварки под флюсом выражение для температуры в столбе дуги имеет вид По длине столба температура принимается постоянной. Для W-дуг (вольфрамовых), горящих в газовой среде (Аг, Не), при приближенной оценке среднюю температуру в центре столба можно принять равной что в аргоне дает Т= 16 000 К, а в гелии Т= 25 000 К. Это хорошо согласуется с экспериментальными данными и соответствует тому факту, что основной плазмообразующий газ в W-дугах - обычно защитный газ, а не пары металла. |
