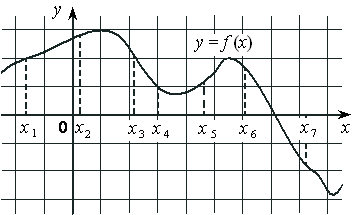Итоговый сборник. институт развития образования и социальных технологий
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
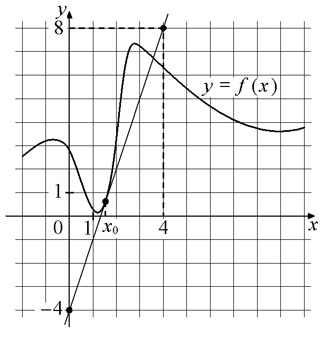
Результаты ЕГЭ остаются одним из главных показателей работы учителя, поэтому каждый стремиться повысить качество математической подготовки школьников, используя для этого различные формы, приемы и технологии. Первоначально это было знакомство с нормативно-правовыми документами, изучение КИМ разных лет, опыта работы других учителей по этой проблеме. Затем начинается поиск и отбор форм и методов обучения, которые мне кажутся эффективными. Итак, моя система работы по подготовке к ГИА: Изучаю весь материал, посвящённый ЕГЭ, приобретаю сборники с материалами ЕГЭ, демоверсии ЕГЭ; убеждаю школьников в том, что если очень постараться, то можно получить вполне приличный балл, главное не упустить время; знакомлю учащихся со структурой теста, временными рамками, нормами оценивания экзаменационной работы, условиями проведения экзамена; в течение всего года знакомлю детей с материалами ЕГЭ, с новыми пособиями, с интернет сайтами. Решаем варианты из сайта Ларина А.А., из открытого банка заданий ЕГЭ; обучаю «технике сдачи теста»: обучаю строгому самоконтролю времени; учу определять трудность заданий; правильно заполнять бланки ответов; приучаю ребят к методу «пристального взгляда» - внимательно посмотри: «Нет ли короткого пути решения? Так как ты ограничен во времени»; учу определять трудность заданий. Сначала прошу учеников просмотреть тест от начала до конца и отметить карандашом те задания, которые кажутся им простыми и лёгкими и выполнить их в «режиме скорости». Затем, отметить 2-3 задания, которые им понятны по формулировке, но требуют большего времени и выполнить их; и только после этого, если останется время, можно поразмышлять над остальными; напоминаю о том, что полученный результат можно проверить подстановкой, т. е. «прикинуть» имеет ли он смысл; целенаправленное сопутствующее и повторение. Неукоснительное знание теоретического материала. На каждом уроке организую повторение через систему упражнений, составленных на основе КИМ ЕГЭ; после объяснения нового материала и его первичного закрепления показываю, какие задания темы выходят на ЕГЭ; долгосрочное домашнее задание. После проверки – работа над ошибками. групповые и индивидуальные консультации; решение тренировочных тестов; работа по тренажерам. решение тематических тестов по содержательным линиям курса; репетиционные ЕГЭ, диагностические тестовые работы. В начале года входные, в конце итоговые, входящие в компетенцию администрации. разработка индивидуальных траекторий подготовки к ЕГЭ. Для лучшего понимания и усвоения темы «Производная» я использую следующие приемы и методы работы: Отработка теоретических понятий (от определения производной, правил вычисления производных, формул дифференцирования до необходимых и достаточных признаков экстремума, возрастания и убывания функций). Для этого, в течение изучения темы, составляем алгоритмы, создаем справочное пособие. Тренажеры (текстовые, мультимедийные) по различным видам задач. Работа в парах, по проверке первичных знаний. Работа с графиками функций и графиками производных (задания из открытого банка ЕГЭ). Самостоятельные и контрольные работы. Тестовые задания, тренировочные варианты. Дифференцированные задания на основе задания №14. Дополнительные методы исследования (без производной, с помощью второй производной). Самостоятельный разбор решения по готовым презентациям. Перед вами таблица результатов ЕГЭ по школе  Уважаемые коллеги, я вам предлагаю поработать над заданиями по рассматриваемой теме. Работать будем группами. I группа - педагоги основных школ, работают над заданиями:
II группа – учителя 10 классов работают над заданиями типа №14, решаемые по алгоритмам:
III группа учителя 11классов будут исследовать функции нестандартными способами.
Работа по группам 15 минут, затем обсуждение, выводы по заданиям. Рефлексия содержания мастер-класса «Корзина идей»: Каждый педагог добавляет свои методические находки по подготовке обучающихся к ЕГЭ, также рекомендации и советы по решению заданий по теме производная. Закончить наше занятие предлагаю следующим образом: Подберите пословицу, с которой ассоциируется наша работа сегодня. Спасибо, уважаемые коллеги, за сотрудничество. Думаю, что слова Пьера Лапласа « То, что мы знаем, - ограниченно, а то чего мы не знаем, - бесконечно» будут побуждать нас к движению вперед. Желаю всем профессионального удовлетворения и личного благополучия. ВЛИЯНИЕ ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ НА ФОРМИРОВАНИЕ ПОЗНАВАТЕЛЬНОГО ИНТЕРЕСА ОБУЧАЮЩИХСЯ К ИЗУЧЕНИЮ МАТЕМАТИКИ В УСЛОВИЯХ ВНЕДРЕНИЯ ФГОС ООО В.В. Карелина, МКОУ «Самохваловская ООШ» Шатровского района, учитель математики В условиях внедрения ФГОС ООО в школе организация занятий по направлениям внеурочной деятельности является важнейшей частью образовательного процесса в школе. Время, отводимое на внеурочную деятельность, используется по желанию учащихся и в формах, отличных от урочной системы обучения. Для реализации в школе по математике доступны следующие виды внеурочной деятельности: познавательная; игровая деятельность; проблемно-ценностное общение. По моему мнению, внеурочная работа по математике является важнейшей составной частью работы по привитию интереса к предмету. Не секрет, что для многих учеников математика не является любимым предметом. Объясняется этот факт многими причинами, в том числе и сложностью материала, подлежащего изучению. Именно поэтому главная задача внеурочной работы – привитие школьникам интереса к математике и воспитанию потребности изучать его. Что косвенно положительно скажется на подготовке и прохождении ГИА. Хорошо организованная и систематическая внеурочная деятельность дает возможность углублять приобретаемые на уроках знания, совершенствовать умения и навыки анализа, расширять математический кругозор школьников, воспитывать и повышать культуру общения, развивать творческий потенциал учащихся, знакомить учащихся с такими факторами предмета, которые не изучаются на уроках, но знание некоторых необходимо в жизни. Она создает благоприятные условия для умственного развития: ученик активнее пользуется справочной литературой для поиска ответов на вопросы углубленного уровня, идет параллельно подготовка ГИА в форме ОГЭ, готовится к мероприятиям познавательного плана по математике. Исходя из основной цели внеурочной деятельности по математике, можно выделить частные задачи, которые решаются учителем в процессе такой деятельности: формирование коммуникативной культуры школьников; расширение и углубление знаний, умений учащихся и формирование интереса в целом; выявление и поддержка математически одаренных учащихся; развитие и совершенствование психологических качеств личности школьников: любознательности, инициативности, трудолюбия, воли, настойчивости, самостоятельности в приобретении знаний. Каждый, творческий работающий учитель, и есть фанат своего предмета. Он ищет новые пути, новые возможности для поддержания интереса, в частности, к математике. Как и многие мои коллеги, я постепенно прихожу к мысли, что изучение математики, особенно в среднем звене, в условиях внедрения ФГОС требует совместных усилий, как со стороны учителя, детей, так и со стороны родителей. В этом случае необходимо полное взаимопонимание всех сторон, участвующих в образовательном процессе. Я считаю, что внеурочная деятельность по предмету имеет в современное время особо важную роль. Ведь математика занимает особое место в образовании человека, что определяется безусловной практической значимостью математики, её возможностями в развитии и формировании мышления человека, её вкладом в создание представлений о научных методах познания действительности. Являясь частью общего образования, среди предметов, формирующих интеллект, математика находится на первом месте. Первоначальные математические познания должны входить с самых ранних лет в наше образование и воспитание Апробируя методические находки коллег, я разработала программу внеурочной деятельности для пятого класса, обучающегося по ФГОС, внося так же коррективы с учетом возраста учащихся, склонных к занятиям математикой и желающих повысить свой математический уровень. Именно в этом возрасте формируются математические способности и устойчивый интерес к математике. Данная программа является частью интеллектуально-познавательного направления дополнительного образования и расширяет содержание программ общего образования. Цель программы – способствовать воспитанию интереса учащихся к математике и формированию когнитивных умений в процессе занятий математического кружка способностей. Образовательные задачи: углубление и расширение знаний учащихся по математике; привитие интереса учащимся к математике; активизировать познавательную деятельность; показать универсальность математики и её место среди других наук. Воспитательные задачи: воспитание культуры личности; воспитание отношения к математике как к части общечеловеческой культуры; воспитание понимания значимости математики для научно – технического прогресса; воспитание настойчивости, инициативы, чувства ответственности, самодисциплины. Развивающие задачи: развитие ясности и точности мысли, критичность мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей; формирование математического кругозора, исследовательских умений учащихся. Программа содержит материал, как занимательного характера, так и дополняющий, расширяющий программу общеобразовательной школы по математике. Большое внимание в программе уделяется истории математики и рассказам, связанным с математикой (запись цифр и чисел у других народов, математические фокусы, ребусы и др.), выполнению самостоятельных заданий творческого характера (составить рассказ, фокус, ребус, задачу с использованием изученных математических свойств), изучению различных арифметических методов решения задач (метод решения «с конца» и др.), выполнению проектных работ. Уделяется внимание рассмотрению геометрического материала, развитию пространственного воображения. Программа кружка рассчитана на один год обучения (34 занятия в течение учебного года). Итогом реализации программы являются: успешные выступления кружковцев на олимпиадах всех уровней, математических конкурсах, международной математической игре-конкурсе «Кенгуру», а также создание брошюры «Математическая шкатулка» (банк нестандартных задач для учащихся 5 класса), где будут собраны задачи по темам всего курса, которые составлены учащимися или взяты из каких-либо источников (книги, журналы, интернет) и их решения, проектные работы учащихся. Содержание разделов I. Занимательная арифметика Тема 1.Запись цифр и чисел у других народов Как люди научились считать. Старинные системы записи чисел. Цифры у разных народов. Римская нумерация. Тема 2.Числа - великаны и числа–малютки Открытие нуля. Мы живём в мире больших чисел. Числа-великаны. Названия больших чисел. Числа–малютки. Решение задач с большими и малыми числами. Тема3. Упражнения на быстрый счёт Некоторые приёмы быстрого счёта. Умножение двухзначных чисел на 11,22,33, . . . , 99. Умножение на число, оканчивающееся на 5. Умножение и деление на 25,75,50,125. Умножение и деление на 111,1111 и т.д. II. Занимательные задачи Тема 1. Магические квадраты. Отгадывание и составление магических квадратов. Тема 2. Математические фокусы. Математические фокусы с «угадыванием чисел». Примеры математических фокусов. Тема 3. Математические ребусы. Решение заданий на восстановление записей вычислений. Тема 4. Софизмы. Понятие софизма. Примеры софизмов. Тема 5. Задачи с числами Запись числа с помощью знаков действий, скобок и определённым количеством одинаковых цифр. Тема 6. Задачи – шутки Решение шуточных задач в форме загадок. III. Логические задачи Тема 1. Задачи, решаемые с конца. Решение сюжетных, текстовых задач методом «с конца». Тема 2. Круги Эйлера. Решение задач с использованием кругов Эйлера. Тема 3. Простейшие графы Понятие графа. Решение простейших задач на графы. Тема 4. Задачи на переливания. Решение текстовых задач на переливание. Тема 5. Взвешивания. Решение задач на определение фальшивых монет или предметов разного веса с помощью нескольких взвешиваний на чашечных весах без гирь. Тема 6. Задачи на движение. Решение текстовых задач на движение: на сближение, на удаление, движение в одном направлении, в противоположных направлениях, движение по реке. Тема 7. Старинные задачи Решение занимательных старинных задач и задач-сказок. IV. Геометрические задачи Тема 1. Задачи на разрезания. Геометрия вокруг нас. Геометрия на клетчатой бумаге. Игра «Пентамино». Тема 2. Задачи со спичками. Решение занимательных задач со спичками. Тема 3. Геометрические головоломки. «Танграм». V. Проекты Тема 1. Выбор тем и выполнение проектных работ. Примерные темы проектов: Системы счисления. Мифы, сказки, легенды. Математические фокусы. Лабиринты. Свои темы проектов. |