Итоговый сборник. институт развития образования и социальных технологий
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Литература: 1. Андреев А.Л. Компетентностная парадигма в образовании: опыт философско-методологического анализа педагогика // Педагогика. – 2005. – № 4. – С.19–26. 2. Косино О.А. Формирование профессиональной компетентности учителя в области элементарной математики в условиях интеграции педагогических и информационных технологий // Современные проблемы науки и образования. – 2009. – № 2. – С. 41. 3. Радионова Н.Ф., Тряпицына А.П. Компетентностный подход в педагогическом образовании // Электронный научный журнал «Вестник Омского государственного педагогического университета», выпуск 2006. 4. Шамшурина А.А. Модель формирования информационно-коммуникационной компетентности будущего учителя // Известия Российского государственного педагогического университета имени А.И.Герцена. - СПб., 2009. – № 112. – С.216 5. Баландин И.А. О направлениях использования интерактивных средств обучения на уроках математики в старших классах / Баландин И.А. // Известия ПГПУ им. В.Г. Белинского. Серия Физико-математические науки. №18(22), 2010г.-С.216-219. 6. Гаврилова М.А. Профильное обучение математике: теория, практика, примеры /М.А. Гаврилова, Н.В. Печникова// – Пенза: ПГПУ, 2008. — 130с. 7. Информационные и коммуникационные технологии в образовании. Учебное пособие / И.В. Роберт, С.В. Панюкова, А.А. Кузнецов, А.Ю. Кравцова. – М.: Дрофа, 2008. – 320 с. РАЗВИТИЕ МАТЕМАТИЧЕСКИХ СПОСОБНОСТЕЙ ОДАРЕННЫХ ДЕТЕЙ В УСЛОВИЯХ РЕАЛИЗАЦИИ КОНЦЕПЦИИ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ В РОССИЙСКОЙ ФЕДЕРАЦИИ И.Г. Парахин ГАОУ ДПО ИРОСТ г. Курган, старший преподаватель кафедры естественно-математического образования Согласно Концепции развития математического образования в Российской Федерации каждому учащемуся необходимо предоставить возможность достижения соответствия любого уровня подготовки с учетом его индивидуальных потребностей и способностей. Для достижения высокого уровня подготовки должна быть развита система математических соревнований. Поэтому по Плану мероприятий реализации Концепции развития математического образования в Российской Федерации предусмотрены математические олимпиады и конкурсы для выявления и поддержки одаренных детей. Самой массовой олимпиадой в стране является Всероссийская олимпиада по математике для школьников. Победителям и призёрам регионального (муниципального) этапа даётся возможность участвовать во Всероссийской олимпиаде по этому предмету с регионального (муниципального) этапа, минуя предыдущие. Победители или призёры заключительного этапа имеют право на поступление без вступительных испытаний в любой вуз на направление, соответствующее профилю олимпиады. Если победитель или призер выбирает образовательную программу по непрофильному направлению, то ему засчитывается наивысший результат по математике – сто баллов. Для них право на льготу сохраняется в течение четырех лет. Приказом Министерства образования и науки Российской Федерации № 901 от 28 августа 2015 года утвержден перечень олимпиад школьников и их уровней на 2015/16 учебный год. Среди них есть Межрегиональная олимпиада школьников «Высшая проба», Межрегиональная олимпиада школьников по математике и криптографии, Открытая олимпиада школьников по математике и другие олимпиады. Победители и призеры этих олимпиад так же могут воспользоваться одной из льгот первого или второго порядка. Льгота первого порядка - поступление без экзаменов, льгота второго порядка - сто баллов по математике. Право на льготу сохраняется в течение одного года. Так, в 2015 году было шестьдесят шесть призеров, которым засчитали сто баллов по математике. При этом не было выпускников, написавших ЕГЭ по математике профильного уровня на сто баллов. Предметные олимпиады способствуют выявлению и развитию одаренных учащихся. По плану мероприятий Курганской области по реализации Концепции развития математического образования в Центре дистанционного обучения ГБОУОШИ «Лицея-интерната для одаренных детей» города Кургана у одаренных сельских школьников есть возможность углубить знания по математике, подготовиться к олимпиадам и различным математическим конкурсам. Лучшие выпускники Центра без экзаменов могут быть зачислены в «Лицей-интернат для одаренных детей». Внимание именно к таким детям неслучайно. Многие ученые родом из глубинки. Например, один из ведущих советских учёных-алгебраистов Каргаполов Михаил Иванович, родившийся в деревне Русакова Каргапольского района Курганской области. Поэтому при работе с одаренными детьми из сельской местности от учителей в первую очередь будет требоваться увлеченность делом, способность к экспериментальной, научной и творческой деятельности, использование передовых педагогических технологий и умелая организация учебно-воспитательного процесса. Одаренность определяется не только уровнем имеющихся у ребенка знаний и умений, но и его потенциальными возможностями. Успешное выполнение заданий повышенного и высокого уровня сложности с развернутым ответом единого государственного экзамена по математике профильного уровня позволяет выявить и поддержать лидеров математического образования на уровне общего образования. В контрольно-измерительных материалах ЕГЭ имеется задание на применение математики на творческом уровне. По результатам ЕГЭ по математике профильного уровня 2015 года по Курганской области это задание полностью выполнили 0,08 % выпускников. Основное отличие данного задания от остальных является его явно выраженный нестандартный характер. Один балл на данной задаче заработали 6,36 % учеников, т.е. у них был потенциал для решения этой задачи, но им не хватило времени или знания нетривиальных методов решения таких задач. В контрольно-измерительных материалах ЕГЭ базового уровня также встречаются творческие математические задания. На ЕГЭ по математике базового уровня 2015 года по Курганской области с задачей по теории чисел справилось 34,59% выпускников, а с более сложной творческой задачей - 14,44%. Т.е. около трети выпускников имели потенциал для решения последней задачи, но не знали способа решения. Чтобы улучшить результаты одаренных детей необходимо руководствоваться следующими принципами: принцип индивидуализации и дифференциации обучения; принцип возрастания роли внеурочной деятельности; принцип создания условий для совместной работы учащихся при минимальном участии учителя; Возможность достижения необходимого уровня математического образования должна поддерживаться использованием электронного обучения и дистанционных образовательных технологий. Необходимо дальнейшее обеспечение условий, способствующих максимальному раскрытию потенциальных возможностей одаренных детей, в том числе оказания адресной поддержки каждому ребенку, проявившему незаурядные способности, разработка индивидуальных «образовательных маршрутов». Учить одаренного ребенка нелегко, но чрезвычайно интересно и увлекательно, ведь, по словам французского философа Мишеля де Монтеня «Для того чтобы обучить другого, требуется больше ума, чем для того чтобы научиться самому». Формирование умения работать с учебным текстом на уроках математики Э.Н. Рогачева, МКОУ «Петуховская СОШ №1», учитель математики Многие учителя математики при проверке самостоятельных и контрольных работ встречались с ситуацией, когда вполне успешный ученик выполняет предложенное задание либо не в полном объеме, либо подменяет задание близким по смыслу или содержанию, либо вообще мысленно его переформулирует, изменив суть задания. В чем причина? Невнимательность, детская фантазия, подмена действительного задания желаемым? Особенно актуальна эта проблема во время прохождения государственной итоговой аттестации, когда свой отпечаток накладывают волнение и ограниченность во времени на выполнение заданий. В результате выпускник теряет драгоценные баллы. Другой причиной заставившей задуматься над проблемой формирования умения работать с учебным текстом являются пропуски занятий обучающимися как по причине болезни, так и практика оздоровления детей в лагерях круглогодичного действия в течение учебного года. Учебный материал, который остался без объяснения учителя, не осваивается в полном объеме и ведет к накоплению «пробелов» в знаниях обучающихся. Хочу поделиться некоторыми эффективными приемами для решения обозначенных проблем. Главной целью считаю формирование у обучающихся умения «добывать знания» со страниц книг и осваивать эти знания, оценивать их, делать их своим внутренним достоянием. Возникает вопрос, умеет ли школьник читать учебник? Ответ на этот вопрос зависит от того, что мы понимаем под умением читать. Обратимся к толковому словарю русского языка. Читать - воспринимать написанное, произнося или воспроизводя написанное про себя. Уметь - обладать способностью делать что-нибудь, быть обученным чему-нибудь. Попытаемся объединить толкование этих слов и получить смысл выражения «уметь читать». Итак, уметь читать — это значит обладать способностью или быть обученным воспринимать написанное. Однако остался нераскрытым смысл слова «воспринимать». Тот же словарь дает следующее толкование. Воспринимать -1) ощутить, распознать органами чувств; 2) понять и усвоить. В результате всех уточнений получаем, что уметь читать учебник означает обладать способностью изначально или быть обученным кем- либо понимать и усваивать представленный в учебнике текст. В практике моей работы с обучающимися 10-11 классов - проведение уроков по следующей схеме: -ученики получают заранее задание: самостоятельно проработать определенный теоретический материал темы, разобрать примеры (их в учебнике А.Г.Мордковича предлагается от 6 до 10) в случае встретившихся затруднений, подготовить вопросы. Следующий урок проходит в форме полилога; помогаю разобраться в особо сложных вопросах, вместе с учащимися проводим анализ, синтез и обобщение изучаемого материала, определяем его место и роль в изучаемом разделе математики. Такие уроки эффективно способствуют формированию личности школьника, так как дети осознают цель, сущность своей учебной работы; осознают, что они уже знают, и что должны узнать; учатся самоконтролю и самооценке, что является важным условием формирования самосознания. Кроме того, на уроках математики, особенно проводимых по описанной схеме, выявляется опыт учеников по отношению к содержанию материала урока. Стимулирую высказывания учеников, которые не боятся ошибиться, получить неправильный ответ. Оцениваю деятельность ученика не только по результату, но и по процессу его достижения. Создаю педагогические ситуации, позволяющие каждому ученику проявить инициативу и избирательность в способах работы, предоставляю возможность самовыражения и творчества. При этом значительно расширяется понятийный аппарат детей и способность понимать научные математические тексты. Учащиеся, которые целенаправленно и систематически обучаются работе с учебным текстом, испытывают потребность в чтении учебника в классе и дома, реализуют свои возможности, участвуя в диалоге на уроке и после урока, ежедневно обогащая себя и других новыми умениями. Особое внимание в процессе подготовке к ГИА уделяю работе с открытым банком заданий. Пополняется копилка приемов самостоятельной подготовки учащихся к выполнению теста. Вот некоторые из них: анализ теста экзаменационной работы в целом и каждого задания в отдельности; составление перечня теоретических положений, необходимых для выполнения заданий; разбиение каждого из заданий на систему простейших; сравнение заданий и способов их решения; составление серии вопросов по тесту и приведение ответов на них; составление заданий, аналогичных данным и их решение; выбор и систематизация заданий, имеющих одинаковый способ решения; решение задания несколькими способами и их сравнение. Одним из критериев при оценке выполнения заданий части 2 является наличие обоснованного и верного ответа. Четкое обоснование может быть представлено таким обучающимся, который хорошо владеет теоретическим материалом, дает аргументированные ответы. Расширить возможности своего математического языка, пополнить запас речевых оборотов можно лишь при внимательном прочтении учебника. Познавательный интерес — это одно из личностных свойств школьника, черта его характера, проявляющаяся в виде пытливости, любознательности, активности. Для правильной организации работы по формированию у учащихся познавательного интереса к математике, нам учителям следовало бы выявить те «за» и «против», которые влияют на этот процесс. Учитель, располагающий такими сведениями, имеет возможность строить свою работу так, чтобы, снимая отрицательные факторы, целенаправленно формировать у школьников познавательный интерес. Около 80% обучающихся 7-8 классов отнесли «неумение понять материал учебника, неумение в нем самостоятельно разобраться» к числу причин, определяющих негативное отношение к математике. Безусловно, процесс формирования познавательного интереса к предмету должен идти через выработку у учащихся умений и навыков работы с учебником математики. Если для разрешения вопроса, возникшего при подготовке к уроку математики, обучающийся обратится ни к ГДЗ, ни к Интернет, а к школьному учебнику, буду считать, что одна из задач стоящих перед учителем математики решена успешно. РАЗВИТИЕ ПРОСТРАНСТВЕННОГО ВООБРАЖЕНИЯ ОБУЧАЮЩИХСЯ НА УРОКАХ ГЕОМЕТРИИ Е.В. Сапожникова, Н.П. Рогова , Н.С. Еланцева, О.С. Москвичева, М.А. Гуржа, преподаватели математики ГБПОУ «Курганский технологический колледж имени Героя Советского Союза Н.Я. Анфиногенова» Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать. Галилео Галилей Хорошо известно: чем выше уровень пространственного представления учащихся, тем проще обучать их геометрии, тем более интересные задачи можно ставить перед ними. К сожалению, приходится обнаруживать у студентов затруднения в моделировании пространственных геометрических фактов и в изображении их. Проблема старая, но актуальная. И если не решать ее в средней школе, то через несколько лет уроки стереометрии с теми же учениками будут терять большую часть своей эффективности. Деятельность учащихся должна быть ориентирована на зарождение, накопление, осмысление и систематизацию геометрической информации. Главная цель – создать запас геометрических представлений, который в будущем должен выступить основой при формировании основных понятий и идей геометрии. Практические задания, приведенные ниже можно использовать на различных этапах уроков геометрии при изучении таких тем, как «Параллельность и перпендикулярность прямых и плоскостей в пространстве», «Многогранники и тела вращения. Их площади поверхностей и объемы» и др. Максимально развивать познавательные способности учащихся, учиться их ориентироваться в простейших геометрических ситуациях и обнаруживать образы в окружающей обстановке возможно при помощи следующих заданий: Задачи на разрезание, перекраивание и складывание фигур Учащиеся располагают линейкой (с делениями), карандашом, ножницами. Разрешается производить с помощью ножниц лишь прямолинейные разрезы. Например: Разделите круглый сыр тремя разрезами на 8 частей. Расположите 5 одинаковых монет так, чтобы каждая из них касалась четырех остальных. Можно ли расположить 6 одинаковых карандашей так, чтобы каждый касался пяти остальных? Геометрические упражнения с листом бумаги Например: Возьмите полоску бумаги и склейте ее края, перевернув один из них на 1800. Получится фигура, которая называется листом Мёбиуса. Чем он замечателен? Задачи со спичками. Для решения занимательных задач со спичками нужны: смекалка, способность предвидеть результат, хорошее воображение. Работа над такими задачами способствует развитию этих качеств у обучающихся. Например: Из шести спичек сложите четыре правильных треугольника так, чтобы стороной каждого была целая спичка. Геометрия и оптические иллюзии. Нередко, решая какие-либо задачи, обучающиеся делают вывод лишь на основании того, что они видят на чертеже; часто даже уверены, что после этого никаких доказательств уже не нужно. Наблюдение над чертежом может нас привести к грубо ошибочным выводам. Например: На левом рисунке любой математик видит куб, а не только два квадрата, вершины которых попарно соединены. А нарисованные все-таки квадраты… Видеть куб нам позволяет хорошо развитое пространственное воображение. Но удивительно: один раз мы видим этот куб как бы сверху и справа (средний рисунок), а другой – снизу и слева (правый рисунок). Это уже казусы иллюзии, которыми надо уметь управлять, подчиняя свое воображение, той реальности, о которой говорится в конкретной задаче. 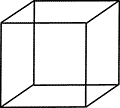 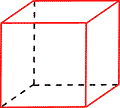 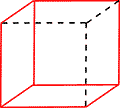 Но многие учащиеся не могут сразу научиться видеть в плоской фигуре выпуклые тела. Т.о., предлагая ряд плоскостных рисунков, пытаемся преодолеть трудности восприятия. Е  ще пара известных иллюзий. ще пара известных иллюзий.Иллюзия Цолльнера (Zolliner, 1860). Параллельные прямые кажутся изогнутыми.  Иллюзия кафе "Wall" . Обнаружена Р. Грегори в кафе "Wall" в Бристоле (Richard Gregory, 1979). Горизонтальные линии параллельны. |
