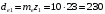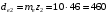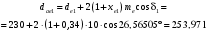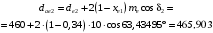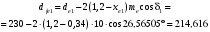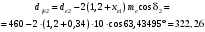Расчет червячного редуктора. Курсовой проект Червяк. Исходные данные 6
 Скачать 2.7 Mb. Скачать 2.7 Mb.
|
3.2 Расчет конической передачиПроектный расчет Внешний делительный диаметр колеса, мм 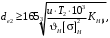 (3.1) (3.1)где u – передаточное число зубчатой пары, 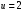 ; ;Т2 – вращающий момент на выходном валу, 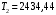 Нм; Нм;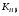 – коэффициент, учитывающий распределение нагрузки по ширине венца, для прирабатывающихся колес с прямыми зубьями – коэффициент, учитывающий распределение нагрузки по ширине венца, для прирабатывающихся колес с прямыми зубьями 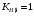 ; ;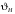 – коэффициент вида конических колес, для прямозубых колес – коэффициент вида конических колес, для прямозубых колес 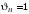 ; ;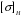 – допускаемое контактное напряжение колеса с менее прочным зубом, – допускаемое контактное напряжение колеса с менее прочным зубом, 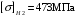 . .Подставляем найденные значения в формулу (3.1), тогда внешний делительный диаметр 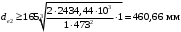 . .Округляем полученное значение до ближайшего числа по таблице 13.15 [1, стр.326] 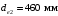 . .Угол делительных конусов колеса  ; ;шестерни 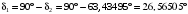 . .Внешнее конусное расстояние 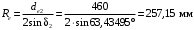 . .Ширина зубчатого венца шестерни и колеса определяется по формуле 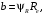 (3.2) (3.2)где 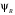 – коэффициент ширины венца, – коэффициент ширины венца, 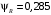 . .Подставляем значения в формулу (3.2), тогда ширина зубчатого венца 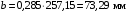 . .Принимаем 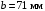 . .Внешний окружной модуль для прямозубых колес определяется по формуле 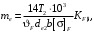 (3.3) (3.3) где 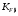 – коэффициент, учитывающий распределение нагрузки по ширине венца, для прирабатывающихся колес с прямыми зубьями – коэффициент, учитывающий распределение нагрузки по ширине венца, для прирабатывающихся колес с прямыми зубьями 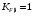 , ,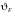 – коэффициент вида конических колес, для прямозубых колес – коэффициент вида конических колес, для прямозубых колес 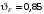 ; ; – допускаемое напряжение изгиба материала колеса с менее прочным зубом, – допускаемое напряжение изгиба материала колеса с менее прочным зубом, 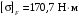 . .Подставляем значения в формулу (3.3), тогда модуль 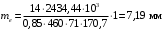 . .Увеличиваем значение модуля на 30%, ввиду повышенного изнашивания зубьев в открытой передаче. Принимаем 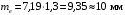 . .Число зубьев колеса 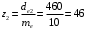 . .Число зубьев шестерни 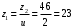 . .Фактическое передаточное число 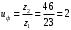 . .Проверяем отклонение от заданного передаточного числа 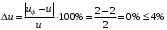 . .Действительные углы делительных конусов колеса 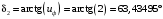 ; ;шестерни 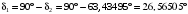 . .Так как 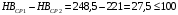 , то по таблице 4.6 [1, стр.71] выбираем коэффициент смещения инструмента для шестерни. , то по таблице 4.6 [1, стр.71] выбираем коэффициент смещения инструмента для шестерни.Таким образом, 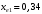 . .Коэффициент смещения колеса 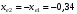 . .Определяем фактические основные геометрические параметры передачи (таблица 3.2). Таблица 3.2 – Основные геометрические параметры передачи Размеры в миллиметрах
Средний делительный диаметр шестерни 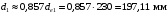 ; ;колеса 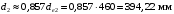 . .Проверочный расчет Условие пригодности заготовок 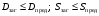 . .Допустимый диаметр заготовки шестерни 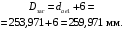 Толщина диска заготовки колеса 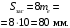 Отсюда 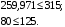 Условие контактной прочности 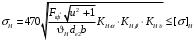 , (3.4) , (3.4)где 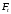 – окружная сила в зацеплении, – окружная сила в зацеплении, 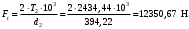 ; ;KH коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых колес, KH = 1; KHυ – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, определяется по таблице 4.3 [1, стр.65]. Окружная скорость колеса 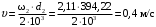 . .Согласно таблице 4.2 [1, стр.64] степень точности передачи равна 9. Учитывая значение окружной скорости и степени точности, принимаем KHυ=1,05. Подставляем найденные значения в формулу (3.4) 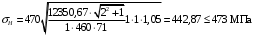 . .Разница между контактным напряжением и допустимым контактным напряжением на колесе 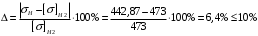 . .Значение не превышает допускаемую недогрузку, следовательно, проверка контактных напряжений выполнена успешно. Проверяем напряжения изгиба зубьев колеса и шестерни. 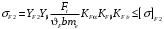 ; (3.5) ; (3.5)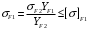 , (3.6) , (3.6)где 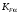 коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых колес KF = 1; коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых колес KF = 1;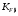 – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся прямозубых колес KF = 1; – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся прямозубых колес KF = 1;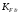 – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, определяется по таблице 4.3 [1, стр.65], принимаем – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, определяется по таблице 4.3 [1, стр.65], принимаем 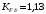 ; ;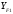 , , 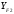 – коэффициент формы зуба шестерни и колеса, определяется по таблице 4.4 [1, стр.67] в зависимости от числа зубьев шестерни и колеса, принимаю – коэффициент формы зуба шестерни и колеса, определяется по таблице 4.4 [1, стр.67] в зависимости от числа зубьев шестерни и колеса, принимаю 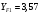 при при 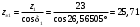 и и 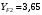 при при 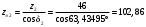 ; ;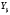 – коэффициент, учитывающий наклон зубьев, для прямозубых колес Y=1. – коэффициент, учитывающий наклон зубьев, для прямозубых колес Y=1.Найденные коэффициенты подставляем последовательно в формулы (3.5, 3.6) 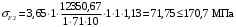 ; ;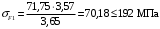 . .Отсюда следует, что проверка по напряжениям изгиба выполнена успешно. |