Строение атома. Периодический закон. Iv строение атома и периодическая система элементов логическая схема главы 154 155
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
|
Пространство, которое включает в себя 90% электронного облака, называется орбиталью. Другими словами, орбиталь – это волновая функция, описывающая состояние электрона. С ее помощью можно рас-считать распределение электронной плотности в заданном пространстве. 169 Волновые функции водородоподобного атома и атома водорода имеют сложный вид и приведены в табл. 4.1 и 4.2. Таблица 4.1 Некоторые волновые функции водородоподобного атома
 170
Таблица 4.2 Некоторые волновые функции электрона в атоме водорода
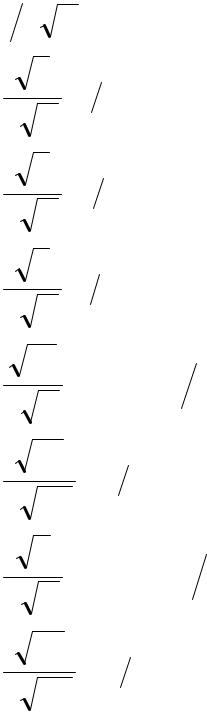 171
Почему мы говорим об электронном облаке, а не об электроне? Электрон наряду с корпускулярными свойствами проявляет и волновые свойства, поэтому его состояние нельзя представить как движение мате-риальной частицы по какой-либо орбите. Квантовая механика рассмат-ривает вероятность пребывания электрона в пространстве вокруг ядра. В качестве квантово-механической модели электрона в атоме принято представление об электронном облаке, плотность соответствующих уча-стков которого пропорциональна вероятности нахождения там электро-на. Чем прочнее электрон связан с ядром, тем меньше должно быть электронное облако по размерам и более плотным по распределению заряда. Существуя в трехмерном пространстве, электрон имеет три степени свободы, а это приводит к тому, что в решении уравнения Шредингера появляются три величины, которые могут принимать только целочис-ленные значения – три квантовых числа, которые обозначаются буквами n, l, m. Тогда результат решения уравнения Шредингера для атома во-дорода можно выразить так: R(r) = f1(n,l); Θ(ϑ) = f2(l,ml); Ф(ϕ ) = f3(m). Квантовые числа n, l, m могут принимать следующие значения:
Рассмотрим возможные значения квантовых чисел n, l и m. n = 1, l = 0 1s – орбиталь, ml = 0 172 Рис. 4.4. Вид s-орбитали S-орбитали характеризуются l = 0 и m = 0, т.е. всего одним значени-ем магнитного квантового числа, определяющего ориентацию подуров-ня в пространстве. Такие орбитали являются безразличными к ориента-ции, имеют максимально симметричную форму – сферическую. Рис. 4.5. Распределение электронной плотности s-орбиталей в зависимости от значения главного квантового числа Если начертить кривые распределения вероятности нахождения электрона для подуровней с l = 0 (т.е. s) для слоев n = 1, n = 2, n = 3 и т.д., то они будут иметь вид, приведенный на рисунке 4.5. Из рис . 4.5 видно, что с удалением слоя от ядра (с увеличением r) вероятности ста-новятся все более размытыми и образуют несколько концентрических орбиталей: для 1s – одну, для 2s – две, для 3s – три, между которыми Ψ 2 = 0. n = 2 l = 0 2s – орбиталь l = 1 2p – орбиталь, ml = -1, 0, +1. Р-орбитали существуют при n ≥ 2 и l = 1 и ориентированы в про-странстве по трем направлениям рx, р y, рz (рис. 4.6) 173 Рис. 4.6. Пространственная ориентация p-орбиталей Электроны , находящиеся на любой из трех р-орбиталей, обладают в изолированном атоме одинаковой энергией. Такое состояние называется вырожденным. Поэтому рx, рy, рz-орбитали являются трижды вырожден-ными, так как они неразличимы по энергии (в изолированном атоме). При приложении магнитного или электронного поля вырождение сни-мается.
d-орбитали характеризуются пятью способами ориентации в про-странстве. Каждая из них изображается в виде "четырехлепестковой розы". d-орбитали ориентированы либо между осями координат 3dxy, 3dxz, 3dyz, либо вдоль осей координат 3dz2, 3dx2 – y2. В изолированном атоме d-орбитали пятикратно вырождены, т. е. все пять атомных d-орбиталей имеют одинаковую энергию (рис. 4.7). 174 Рис. 4.7. Пространственная ориентация d-орбиталей
4f-орбитали изображаются в виде восьмилепестковых фигур и имеют три узловых плоскости. Часто электронным уровням, соответствующим главным кванто-вым числам, присваивают определенные буквенные обозначения: n = 1 K-уровень; n = 2 L-уровень; n = 3 M-уровень; n = 4 N-уровень; n = 5 P-уровень. Квантовые числа характеризуют движение электронов не только в атомах водорода, но и в любых других атомах. Эти характеристики важ-ны для понимания свойств веществ и природы химической связи. По-этому рассмотрим их более подробно. Квантовые числа n,l,m определяют геометрические особенности электронного облака. Они также связаны с физическими характеристи-ками движения электрона. Квантовое число n – это главное квантовое число. Оно определяет энергию электрона. Квантовое число n равно числу узловых поверхно-стей орбиталей. 175 Узловой поверхностью орбитали называется геометрическое место точек, для которых Ψ = 0. Так как Ψ = 0, то и Ψ 2 = 0. Таким образом, на узловой поверхности плотность электронного облака равна нулю. В число узловых поверхностей включается также поверхность, лежащая на бесконечном удалении от ядра. Существование узловых поверхностей в распределении электрон-ной плотности связано с общими закономерностями микромира. Движе-ние микрочастиц описывается соотношениями, аналогичными уравне-ниям волновой механики. В любой волне имеются точки, где смещение колеблющейся величины равно нулю. Если колебательный процесс про-исходит в трех измерениях, то совокупности данных точек образуют узловую поверхность. Рис. 4.8. Вид узловых поверхностей орбиталей Узловые поверхности бывают двух типов: не проходящие через центр атома (ядро) и проходящие через него. Первые являются сферами, центр которых совпадает с ядром, вто-рые являются плоскими или коническими поверхностями. Рис. 4.9. Вид узловых поверхностей орбиталей, не проходящих через центр ато-ма (а) и проходящих через центр атома (б) 176 Наличие сферических узловых поверхностей проявляется в ради-альной части волновой функции – на определенных расстояниях от ядра
Величина l показывает, сколько узловых поверхностей волновой функции электрона проходит через ядро. Мы уже знаем, что одна из узловых поверхностей всегда лежит на бесконечно большом удалении от ядра . Отсюда понятно, почему l изменяется от 0 до (n-1). Квантовое число l определяет симметрию орбитали. Все s-орбитали (l = 0) сферические. p-орбитали (l = 1) имеют форму гантели; d-орбитали (l = 2) – четырехлепестковой розы и т.д. Квантовое число l часто называют орбитальным; оно определяет величину орбитального момента импульса электрона М = ћ √ l(l+1) ћ = h/2π .  Электрон, в соответствии с представлениями квантовой механики, может находиться на любом расстоянии от ядра, но вероятность его пребывания в разных местах атома различна. Зная распределение электронной плотности, можно вычислить среднее расстояние электрона от ядра rср, которое характеризует размер орбитали (орбитальный радиус) . Величина rср определяется значениями n и l. Так, для электрона в атоме водорода rср = (a0n2)/z{1 +0.5[1 – (l(l + 1))/n2]}, где z – заряд ядра; rср пропорционально n2, т.е. значения n определяют размер орбиталей электрона; а 0 = rср = 0.53 °А – т.е. максимальная плот-ность 1s-электрона совпадает с радиусом соответствующей боровской орбиты. Квантовое число ml характеризует расположение орбитали в про-странстве. Его еще называют магнитным, так как оно определяет проек-ции орбитального магнитного момента электрона на ось атома. Магнит-ное квантовое число характеризует ориентацию электронных облаков по отношению к магнитной оси атома. Электрон, как и всякий электрический заряд, движется по замкну-тому контуру, имеет собственный магнитный момент. Величина проек-ции этого момента на одну любую ось координат во внешнем магнит-ном поле принимает определенные квантовые значения, которые и характеризуют расположение подуровня в пространстве. Каждый поду- 177 ровень в уровне имеет столько значений ориентации, сколько значений имеет m. Для каждого подуровня ml = 2l +1, от l = -1 до l = +1. Так, для l = 0 m = 0, т.е. одно значение, l = 1 m = -1,0,+1, т.е. три значения, l = 2 m = -2,-1,0,+1,+2 пять значений, l = 3 m = -3,-2,-1,0,+1,+2,+3 семь значений. Таким образом, каждый подуровень состоит из ориентированных в про-странстве областей, в которых наиболее вероятно нахождение электрона (атомные орбитали – АО). Графически атомные орбитали обозначают     или .  Кроме квантовых чисел n, l, m, известно еще одно. Это так назы-ваемый спин (S) электрона. Упрощенно он показывает вращение элек- трона вокруг собственной оси. Тонкие исследования показали, что электрон обладает не только электростатическим полем, но и магнитными свойствами. Если пропус-тить пучок электронов через сильно изменяющееся магнитное поле, то он распадается на два пучка . Степень отклонения свидетельствует о том, что каждый электрон ведет себя как маленький магнитик, который ори-ентирован по полю либо параллельно, либо в строго противоположном направлении (антипараллельно). Магнитное состояние квантуется, и существуют только два возможных состояния. В микромире магнитное поле возникает при движении электрического заряда по кривой траекто-рии. Предполагается, что в электроне заряд каким-то образом вращает-ся, т.е. говорят, что электрон имеет спин. Это предположение позволяет вычислить магнитное поле, создаваемое спином. Но полученный ре-зультат оказывается вдвое больше экспериментальной величины. Поче-му? При вращении электрона угловой момент определяется распреде-лением массы, а магнитное поле – распределением заряда. Если распре-деление заряда и масса не идентичны друг другу, то классические вы-числения дадут неверное соотношение между угловым моментом и магнитным полем. А это наблюдается и на самом деле. S = ±1/2. Величина 1/2 представляет собой коэффициент расхожде-ния между экспериментом и простым расчетом для отношения момента к полю. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
