Строение атома. Периодический закон. Iv строение атома и периодическая система элементов логическая схема главы 154 155

• Название: Iv строение атома и периодическая система элементов логическая схема главы 154 155
• Дата: 23.06.2019
• Размер: 1.71 Mb.
• Имя файла: Строение атома. Периодический закон.doc
• Тип: Глава; #82704
• страница: 2 из 10

Двойственная природа микрочастиц

• 
  1924 г. французский физик Луи де Бройль предположил, что не только излучение, но и материальные частицы обладают двойственной природой, т. е. свойствами волны и частицы. Размышляя над природой квантования, де Бройль предположил, что для электрона характерны свойства электромагнитных волн, и для него можно рассчитать длину волны. Кроме того, де Бройль предположил, что длина волны электрона укладывается целое число раз на орбите, т.е. сопоставил её со стоячей волной. Примером стоячей волны могут служить колебания скрипичной струны, закрепленной на обоих концах. Струна может колебаться только
  
• 
  определенными частотами. Когда волна колеблется как одно целое, то издает основной тон, при колебаниях с более короткими длинами волн издаются обертоны. Колебания с длиной волны, при которой амплитуда не становится равной нулю на концах закрепленной струны, не могут осуществляться (рис. 4.2).
  

162

	а)	б)
A(x)		в)	1n=4
	λ=2α	λ=4α
	λ=α	λ=4/3α
		г)	1n=4	1
	λ=2/3α	λ=4/5α		3

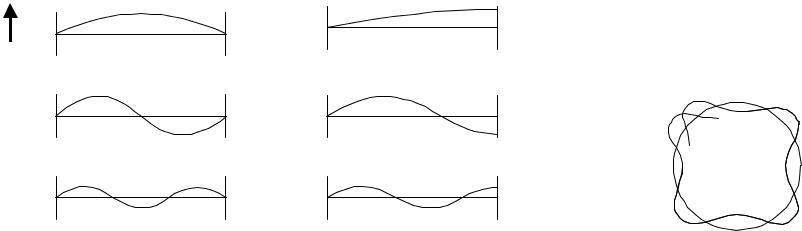Рис.4.2. Приемлемые (а) и неприемлемые (б) стоячие волны, приемлемые (в) и неприемлемые (г) электронные волны
Мы уже видели, что для фотона существует связь между волновыми и корпускулярными свойствами уже в выражении для его энергии:

E = hν ,

(10)

• 
  – это частота, связанная с волновым движением, а Е – энергия, которая может быть выражена через корпускулярные характеристики, такие как масса и скорость.
  

По уравнению Эйнштейна

Е = mc2,	(11)
где с – скорость света.
Приравнивая уравнения (10) и (11), получим:
hν = mc2.	(12)
Переходя к длине волны света
ν = c/λ ,	(13)
получим
h/λ = mc λ = h/mc.	(14)

Отсюда, переходя к частице с массой m и скоростью v, получим:

λ = h/mv.

(15)

Длину волны такой частицы часто называют длиной волны де Бройля. Исходя из формулы де Бройля, можно определить длину волны любой материальной частицы, необходимо только знать ее кинетиче-

163

скую энергию и скорость. Кинетическую энергию определяют экспери-ментально:

_E=mv²

2

• 
  для электрона на К-уровне или на первой орбите атома водорода равна 0.218 ⋅ 10^-10 эрг, или 0.218 ⋅ 10^-17 Дж. Отсюда:
  

V =	2E	;
	m
λ =	h			6,62 ⋅10− 27
	2mE		=	2 ⋅ 9,1⋅10− 28 ⋅ 0,218 ⋅10− 10 = 3,33 Å.

Таким образом, длина волны электрона на первой орбитали атома водорода равна 3,33 Å, r = 0,53 Å. Длина окружности l = 2π r, отсюда для наружной орбиты l = 3.33 Å. Следовательно, длина волны электрона совпадает с окружностью орбиты. Отсюда вывод: на стационарных ор-битах, допускаемых квантовой механикой, длина волны электрона укла-дывается целое число раз, что подтвердило предположение де Бройля.
Если рассчитать длину волны для макрочастиц, например частицы массой 1 г, движущейся со скоростью 1 см/с, то получим λ = 6.6 ⋅ 10^-27 см. Это означает, что волновые свойства макрочастиц практически не проявляются.
Предположение де Бройля было подтверждено экспериментально.

• 
  1927 г. американские физики Девиссон и Джермер, а также Томсон (Англия) и П.С. Тартаковский (СССР) наблюдали дифракцию электро-нов на кристаллах металлов (кристалл никеля). В 1929 г. Штерн обна-ружил сходную дифракцию при прохождении через вещество атомных и молекулярных пучков.
  

Принцип неопределенности

• 
  волновых свойствах электрона заложен первый принцип волно-вой механики. Вторым принципом является принцип неопределенности Гейзенберга (1925 – 1927 гг.).
  

Согласно этому принципу невозможно точно определить местопо-ложение частицы и ее импульс.

Чем точнее определяется координата частицы, тем более неопреде-ленным становится ее импульс, и, наоборот, чем точнее известен им-пульс, тем неопределеннее координата.

164

Если мы утверждаем, что определенный объект – частица, то мы должны уметь измерить корпускулярные свойства этого объекта (на-пример, скорость и положение в пространстве). Это было бы нетрудно сделать, если бы объектом служил мяч, но для электрона измерение этих величин требует особого подхода.

Допустим, что у нас есть какой-то микроскоп, позволяющий уви-деть движущийся электрон. Сначала электрон движется прямо. Однако как только он столкнется с фотоном, имеющим сравнимую массу, то изменятся направление движения и скорость движения электрона. По-этому, наблюдая через малые промежутки времени, можно заметить, что электрон движется зигзагообразно под влиянием ударов фотонов.
Для уменьшения влияния столкновения можно уменьшить энергию фотонов. Но это приведет к увеличению длины волны света Е = ћν , λ = c/ν , что уменьшит разрешающую способность микроскопа (т.е. точ-ность, с которой можно определить положение электрона), зависящую от длины волны излучения.

Таким образом, используя свет большой длины, мы точно узнаем скорость электрона, но его положение точно определить не можем. С другой стороны, свет с короткой длиной волны, состоящий из фотонов высокой энергии (E = ћν ), позволяет точно определить положение элек-трона , но его скорость определить нельзя, так как на скорость электрона будут сильно влиять столкновения с фотонами.
Таким образом, чем точнее определяем мы положение электрона в пространстве, тем неопределеннее его скорость, и наоборот, чем точнее определяем мы скорость электрона, тем более неопределеннее положе-ние электрона . Мы не можем одновременно точно определить положе-ние частицы и ее скорость.
Соотношение неопределенностей имеет вид:

∆Χ ⋅ ∆ V ≥	"	" =	h	, (16)
	m		2π
	!

где ∆ x – неопределенность положения частицы; ∆ v – неопределенность скорости. Таким образом записывается принцип Гейзенберга (1927).
Принцип неопределенности делает невозможным утверждение, что электрон, имеющий определенную скорость, находится в том или ином месте пространства. Мы можем только говорить о вероятности нахож-дения электрона в том или ином месте пространства.

165

Пример: Для электрона,движущегося по орбите со скоростью1056м/с, рассчитайте импульс и неопределенность по импульсу.
Решение: Допустим,что мы можем измерить положение электрона

• 
  точностью до 0,01 Å, что составляет примерно 1% от типичного раз-мера атома. Тогда
  

• 
  = mv = 10^-30 кг 10⁶ м/с = 10^-24 кгм/с.
  

Согласно принципу неопределенности Гейзенберга неопределен-ность определения импульса составит:

	h		0,5 ⋅10− 34
P =	2π	=		= 0,5	⋅10− 22	кгм/с
	X		0,01⋅10− 10

Отсюда видно, что неопределенность по импульсу в 50 раз больше самого импульса.
Уравнение Шредингера

• 
  1925-1926 гг. Гейзенберг и Шредингер независимо друг от другa предложили два варианта новой механики. Оба варианта приводят к аналогичным результатам, но метод Шредингера оказался более удоб-ным для выполнения расчетов, и поэтому современная теория строения атомов и молекул основывается на этом методе. Механика микрообъек-тов получила название квантовой механики, в отличие от классической механики, применяемой к макрообъектам.
  

Законы движения частиц в квантовой механике выражаются урав-нением Шредингера:

h2

d 2Ψ

d 2

Ψ

d 2

Ψ

−

⋅

+

+

+ UΨ = EΨ

,

(17)

2

2

2

2

8π

m

dx

dy

dz

где h – постоянная Планка, m – масса частицы, U – потенциальная энер-гия частицы, E – полная энергия, x,y,z – координаты частицы.
Уравнение Шредингера описывает общие законы движения микро-частицы и является одним из постулатов квантовой механики. Справед-ливость этого уравнения подтверждается согласием с опытом . Уравне-ние Шредингера играет в квантовой механике ту же роль, что и законы Ньютона в классической механике. Как и законы Ньютона, это уравне-ние невозможно вывести из каких-либо общих положений. Оно может

166

быть получено, исходя из определенной аналогии между уравнениями механики и оптики. Его можно получить, если в дифференциальное уравнение волны подставить λ из уравнения де Бройля и выразить им-пульс частицы через разность полной и потенциальной энергий.

Познакомимся с математическим описанием волнового движения. Рассмотрим плоскую (одномерную) волну, которая с течением времени передвигается по оси Х (рис. 4.3.):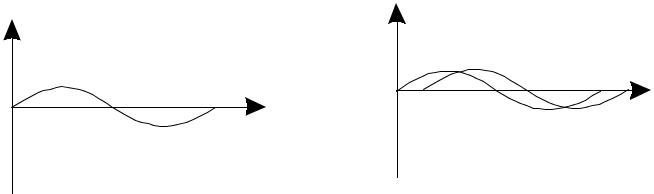




Х

Х

Рис. 4.3. Плоская одномерная волна
Это волновое движение можно выразить уравнением:

d 2Α	=	1	⋅	d 2Α	,	(18)
dx2		c		dt 2

где А – амплитуда волны; с – скорость движения волны; t – время. Решая это уравнение для одномерной волны, можно определить
амплитуду А во время t и в положении x:

2π

x

Α =

2a sin

⋅ cos 2π

yt ,

(19)

λ

где а – константа; λ

– длина волны.

Для трехмерного пространства дифференциальное уравнение имеет

вид:

d 2Ψ

+

d 2Ψ

+

d 2Ψ

+

4π

2

Ψ = 0

,

(20)

dx2

dy2

dz2

λ

2

где Ψ – это трехмерный аналог А. Это уравнение Шредингер выбрал как основу для описания строения атома, так как, согласно гипотезе де Бройля, электрон – это стоячая волна.
Поэтому, подставляя в волновое уравнение для трехмерной волны длину волны де Бройля, получим:

167

d 2Ψ

+

d 2

Ψ

+

d 2

Ψ

+

4π

2m2v2

= 0

,

(21)

dx2

dy2

dz2

h2

Учитывая, что полная энергия электрона в атоме является суммой потенциальной U и кинетической mv²/2 энергий

E =

mv2

U ,

+

(22)

2

можно исключить v2

из уравнения волны и получить:

d 2Ψ

+

d 2Ψ

+

d 2Ψ

+ ( E −

U)Ψ =

0

(23)

dx2

dy2

dz2

или

d 2Ψ

+

d 2

Ψ

+

d 2Ψ

+

2m

(E −

U )Ψ =0.

(24)

dx2

dy2

dz2

h2

Это уравнение и называется уравнением Шредингера. Часто оно за-писывается в следующем виде:

−	h2	d 2Ψ		+	d 2Ψ	+	d 2Ψ		+ UΨ = EΨ ,	(25)
	2m		dx2		dy2		dz2

где h – постоянная Планка; m – масса частицы; U – потенциальная энер-гия; E – полная энергия; x,y,z – координаты частицы.
Это уравнение можно записать и по-другому:

−

h2

V 2Ψ

+ UΨ

= EΨ ,

(26)

2m

где ∇

2

=

d 2Ψ

+

d 2

Ψ

+

d 2Ψ

– оператор Лапласа.

dx2

dy2

dz2

Очень часто уравнение Шредингера изображают в краткой форме:

HΨ

= EΨ

,

(27)

где H – оператор Гамильтона, или оператор полной энергии.

H = −

h2

d 2Ψ

d 2Ψ

d 2Ψ

+ UΨ = EΨ

⋅

+

+

,

(28)

2m

dx2

dy2

dz2

или

Н = –h2/2m ∇ 2Ψ

+ UΨ .

(29)

168

Величина Ψ называется волновой функцией. Ее квадрат имеет оп-ределенный физический смысл: величина Ψ ²dV пропорциональна веро-ятности нахождения электрона в элементарном объеме пространства с координатами x, y, z.
Величину Ψ ² называют плотностью вероятности, или электронной плотностью.
Волновая функция должна быть конечной, непрерывной и одно-значной, а также обращаться в нуль там, где частица не может нахо-диться.
Волновые функции, являющиеся решениями уравнения Шрединге-ра, могут быть сложными функциями пространственных переменных и времени. Они зависят от конкретного вида движения частицы. Кванто-во-механическая теория атома и молекулы сводится к нахождению удовлетворяющих уравнению Шредингера волновых функций и значе-ний энергии Е.
Рассмотрим решение уравнения Шредингера в потенциальном поле ядра. Примером такой системы является атом водорода.
Решения уравнения Шредингера для атома водорода были получе-ны в 1927 г. Эти решения приводят к понятию атомной орбитали, кван-товых чисел и квантованию энергий, которые являются фундаменталь-ными в современной теории строения атома.
Для простейшей электронной системы – атома водорода – решение уравнения Шредингера в полярных координатах дает волновую функ-цию общего вида:

Ψ = N [R(r)][Θ(ϑ)Φ (ϕ )],

(30)

где N – постоянная нормировки, задается стопроцентной вероятностью нахождения электрона где-либо в пространстве около ядра;
R(r) – радиальная часть волновой функции, возведенная в квадрат, показывает вероятность нахождения электрона в радиальном направле-нии от ядра на расстоянии r;
Θ(ϑ)Φ (ϕ ) или Ф(x/r, y/r, z/r) – угловая часть волновой функции – определяет форму поверхностей, ограничивающих пространство, в ко-тором вероятность нахождения электрона составляет не менее 90%.