Новиков учебник. Изложение одноименной книги
 Скачать 101.59 Kb.
|
|
Порядковая шкала. Если использовалась порядковая шкала (шкала рангов) с L градациям (напри- мер, в пятибалльной школьной шкале L = 5), то будем считать, что {xi} и {yj} – натуральные числа, принимающие одно из L значений. Для простоты можно считать, что множество значений (баллов) есть множество чисел от единицы до L. Тогда характеристикой группы будет число ее членов, набравших заданный балл. То есть, для экспериментальной группы вектор баллов есть n = (n1, n2, …, nL), где nk– число членов экспериментальной группы, получивших k-ый балл, k = 1, 2, …, L. Для контрольной груп- пы вектор баллов есть m = (m1, m2, …, mL), где mk– число членов контрольной группы, получивших k- ый балл, k = 1,2, …,L. Очевидно, что n1+ n2 + … + nL= N, m1+m2+…+mL=M. Пусть в рассматриваемом примере (в котором (N = 25, M = 30) выделены три уровня знаний (L = 3): низкий (число решенных задач меньше либо равно 10), средний (число решенных задач строго больше 10, но меньше либо равно 15) и высокий (число решенных задач строго больше 15). Сформируем в компьютерной программе Microsoft Excel для Windows таблицу 2, в которой указаны верхние границы диапазонов. Таблица2 Переход от шкалы отношений к порядковой шкале
Поставим в соответствие уровням знаний (низкому, среднему и высокому) баллы – 1, 2 и 3. Вычис- лим на основании данных таблицы 1, например, сначала для контрольной группы до начала экспери- мента число ее членов, получивших балл, принадлежащий тому или иному диапазону: m1 = 9 (то есть, 9 членов контрольной группы до начала эксперимента продемонстрировали низкий уровень знаний), m2 = 14, m3= 7. Результаты8 занесем в таблицу 3. Таблица3 Уровни знаний членов контрольной группы до эксперимента
Для каждого из столбцов таблицы 1 по аналогии с таблицей 3 определяем распределение членов экспериментальной и контрольной групп по уровням знаний и получаем таблицу 4. Таблица4 Результаты измерений уровня знаний в контрольной и экспериментальной группах до и после эксперимента
Таблица 4 построена по таблице 1 введением диапазонов значений числа правильно решенных за- дач, попадание в которые считалось соответствующим уровням знаний. Отметим, что при подобном переходе от шкалы отношений к порядковой шкале часть информации теряется – в рассматриваемом примере одному и тому же уровню знаний соответствуют несколько различных чисел правильно ре- шенных задач. Следовательно, труднее становится устанавливать совпадения и различия характеристик исследуемых объектов. Поэтому, рекомендуется использовать всю имеющуюся информацию, то есть, если при измерениях использовалась шкала отношений, то и обрабатывать данные следует в этой шка- ле. Однако, во многих случаях на практике измерения производят в порядковой шкале (например, оце- нивают знания в баллах), и результаты эксперимента сразу имеют вид таблицы типа таблицы 4. Поэто- му для задач анализа результатов измерений, произведенных в шкале отношений, будем считать, что данные эксперимента имеют вид таблицы 1, а для задач анализа результатов измерений, произведенных в шкале порядка, будем считать, что данные эксперимента имеют вид таблицы 4. 8В компьютернойпрограммеMicrosoftExcelдляWindowsтаблица3получаетсяизтаблиц1и2применениеминструментаанализаданных"Гистограмма"(Меню/Сервис/Анализданных/Гистограмма). Типовые задачи анализа данных. Завершив описание используемых в качестве примера исходных данных, отметим, что с точки зрения их анализа можно выделить тритипазадач: описание данных (компактное и информативное отражение результатов измерений характеристик исследуемых объектов); установлениесовпаденияхарактеристик двух групп; установлениеразличияхарактеристик двух групп (например, экспериментальной и контрольной). Два типа шкал (отношений и порядка) и три перечисленные типа задач анализа данных позволяют выделить шесть базовых (типовых) задач, приведенных в таблице 5 и условно обозначенных "зада- ча 1.1" – "задача 2.3". Например, задача 1.1 заключается в описании данных, измеренных в шкале отно- шений и т.д. Таблица5 Типовые задачи анализа данных
Перечисленные шесть задач являются базовыми по следующим причинам. Во-первых, они вклю- чают большинство (порядка 90 %) задач анализа данных, встречающихся в экспериментальных иссле- дованиях по педагогическим наукам. Во-вторых, они сформулированы для простейшей схемы органи- зации педагогического эксперимента – когда состояние исследуемых объектов описывается одним показателем и измеряется два раза – до начала и после завершения воздействия. Сделаем пояснение для других случаев. Если возникает многокритериальность (объекты описываются одновременно по нескольким крите- риям), то описание и сравнение экспериментальной и контрольной групп9 по каждому из критериев может производиться независимо в рамках одной из базовых задач. Аналогично, если возникает динамика (то есть, состояния объектов измеряются более чем два раза), то описание и сравнение групп может производиться несколько раз независимо (в каждый момент вре- мени) в рамках одной из базовых задач 1.1-2.3 (см. таблицу 5). Если же у исследователя имеется желание сразу анализировать одновременно несколько групп (в динамике) и/или несколько показателей, то необходимо применение статистических методов много- мерного анализа. Их описание выходит за рамки настоящей работы, ознакомиться с ними можно в пуб- ликациях, перечисленных в упомянутой во введении работе автора. Рассмотрим методы решения типовых для педагогических исследований задач анализа данных. Алгоритм выбора статистического критерия. Поясним, как следует выбирать статистические критерии, то есть приведем алгоритм выбора статистического критерия – процедуру принятия решения относительно того, какой статистический критерий использовать в той или иной ситуации. В первом приближении этот алгоритм чрезвычайно прост: если данные получены в результате измерений в шкале отношений, то следует использовать критерий Вилкоксона-Манна-Уитни (ВМУ), если в порядковой шкале, то критерий c 2. Возможные модификации этого правила принятия решений (учитывающие большее число факто- ров) приведены на рисунке 1. Во-первых, необходимо определить какая шкала измерений используется – отношений или поряд- ковая. Для шкалы отношений следует решить, состоит ли решаемая задача в обнаружении различия сред- них значений (математических ожиданий). Если – да, то можно использовать критерий Крамера-Уэлча (описание методик применения всех упоминаемых статистических критериев приведено ниже). Если же следует обнаружить произвольные различия характеристик выборок, то следует использовать критерий Вилкоксона-Манна-Уитни или критерий 2. Если число различающихся между собой значений10 в сравниваемых выборках велико (более деся- ти), то целесообразно использование критерия Вилкоксона-Манна-Уитни. 9Встречаютсяслучаи,когдаимеетсянесколькоэкспериментальныхилинесколькоконтрольныхгрупп.Приэтомпопарноеих сравнениевсеравноявляетсяодной из базовыхзадач. 10Например,выборка(1,2,2,2, 1, 1, 2,1, 1, 1) содержитвсегодваразличныхзначения–единицуидвойку.Втожевремя, например,выборка (2,0,1,5,8,4,2,7,3,9) того жеобъема(десять элементов) содержитдесять различныхзначений. Если число различающихся между собой значений в сравниваемых выборках мало (менее десяти), то, произведя группировку результатов измерений (то есть, перейдя от шкалы отношений к порядковой шкале – см. выше пятый раздел), можно использовать критерий 2. Далее, аналогично рассуждая, если объем выборок мал11 (N, M 50), то следует использовать кри- терий Вилкоксона-Манна-Уитни (при малом числе различающихся значений в этом случае можно ис- пользовать и критерий 2).   Если объем выборок велик, то, опять же с помощью группировки результатов измерений, имеет смысл использовать критерий 2.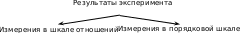
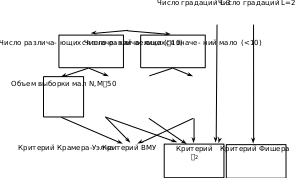  Рис.1.Алгоритмвыборастатистическогокритерия Для порядковой шкалы в случае, когда число градаций (различных баллов) больше либо равно трем, используется критерий 2, если же применялась дихотомическая шкала, то можно использовать либо критерий 2, либо критерий Фишера. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
