Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
 Скачать 4.07 Mb.
|
Лекция 26 Параметрическая статистическая идентификация (часть 5)Оценивание параметров и состояния объектов Фильтр Калмана-Бьюси. (Калмановская фильтрация). Винеровские фильтры лучше всего подходят для обработки процессов или отрезков процессов в целом (блочная обработка). Для последовательной обработки требуется текущая оценка сигнала на каждом такте с учетом информации, поступающей на вход фильтра в процессе наблюдения. При винеровской фильтрации каждый новый отсчет сигнала потребовал бы пересчета всех весовых коэффициентов фильтра. В настоящее время широкое распространение получили адаптивные фильтры, в которых поступающая новая информация используется для непрерывной корректировки ранее сделанной оценки сигнала (сопровождение цели в радиолокации, системы автоматического регулирования в управлении и т.д). Особенный интерес представляют адаптивные фильтры рекурсивного типа, известные как фильтр Калмана. Эти фильтры широко используются в контурах управления в системах автоматического регулирования и управления. Именно оттуда они и появились, подтверждением чему служит столь специфическая терминология, используемая при описании их работы, как пространство состояний. Одна из основных задач, требующих своего решения в практике нейронных вычислений, – получение быстрых и надежных алгоритмов обучения НС. В этой связи может оказаться полезным использование в контуре обратной связи обучающего алгоритма линейных фильтров. Так как обучающие алгоритмы имеют итеративную природу, такой фильтр должен представлять собой последовательное рекурсивное устройство оценки. Задача оценки параметров Одной из задач теории статистических решений, имеющих большое практическое значение, является задача оценки векторов состояния и параметров систем, которая формулируется следующим образом. Предположим, необходимо оценить значение векторного параметра X, недоступного непосредственному измерению. Вместо этого измеряется другой параметр Z, зависящий от X. Задача оценивания состоит в ответе на вопрос: что можно сказать об X, зная Z. В общем случае, процедура оптимальной оценки вектора X зависит от принятого критерия качества оценки. Например, байесовский подход к задаче оценки параметров требует полной априорной информации о вероятностных свойствах оцениваемого параметра, что зачастую невозможно. В этих случаях прибегают к методу наименьших квадратов (МНК), который требует значительно меньше априорной информации. Рассмотрим применения МНК для случая, когда вектор наблюдения Z связан с вектором оценки параметров X линейной моделью, и в наблюдении присутствует помеха V, некоррелированная с оцениваемым параметром: (26.1) где H – матрица преобразования, описывающая связь наблюдаемых величин с оцениваемыми параметрами. Оценка X, минимизирующая квадрат ошибки, записывается следующим образом: (26.2) Пусть помеха V не коррелированна, в этом случае матрица RV есть просто единичная матрица, и уравнение для оценки становится проще: (26.3) Запись в матричной форме сильно экономит бумагу, но может быть для кого-то непривычна. Следующий пример, взятый из монографии Коршунова Ю. М. "Математические основы кибернетики", все это иллюстрирует. Имеется следующая электрическая цепь: 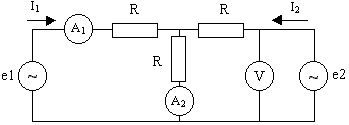 Наблюдаемые величины в данном случае – показания приборов A1 = 1 A, A2 = 2 A, V = 20 B. Кроме того, известно сопротивление R = 5 Ом. Требуется оценить наилучшим образом, с точки зрения критерия минимума среднего квадрата ошибки значения токов I1 и I2. Самое важное здесь заключается в том, что между наблюдаемыми величинами (показаниями приборов) и оцениваемыми параметрами существует некоторая связь. И эта информация привносится извне. В данном случае, это законы Кирхгофа, в случае фильтрации (о чем речь пойдет дальше) – авторегрессионная модель временного ряда, предполагающая зависимость текущего значения от предшествующих. Итак, знание законов Кирхгофа, никак не связанное с теорией статистических решений, позволяет установить связь между наблюдаемыми значениями и оцениваемыми параметрами (кто изучал электротехнику – могут проверить, остальным придется поверить на слово): 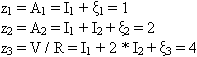 Это же в векторной форме: Или Z = HX + V, где 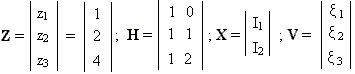 Считая значения помехи некоррелированными между собой, найдем оценку I1 и I2 по методу наименьших квадратов в соответствии с формулой 3: 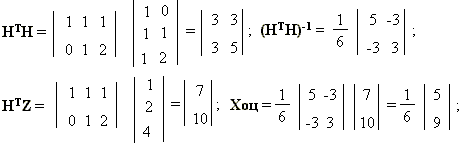 Итак I1 = 5/6 = 0,833 A; I2 = 9/6 = 1,5 A; Оценивание состояния фильтром Калмана Для учёта погрешности измерения, погрешности моделирования вектора состояния и влияния на систему случайных факторов воспользуемся дискретным фильтром Калмана для оценки вектора состояния. Текущие значения оценок вектора состояния 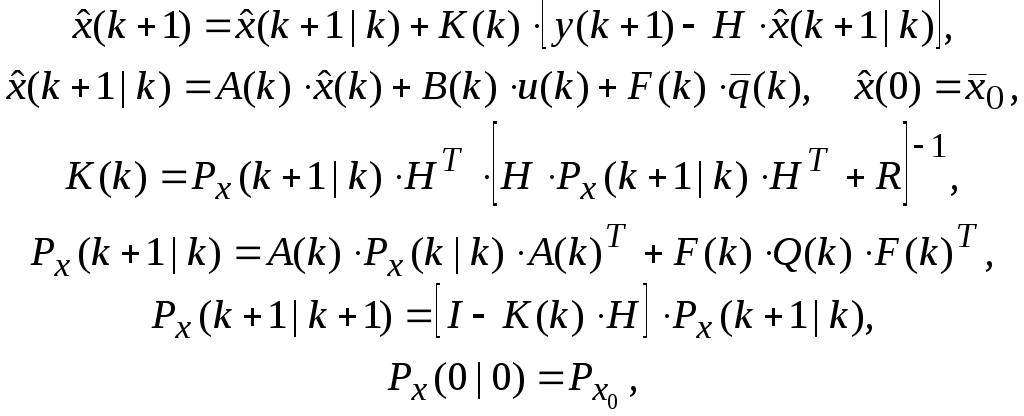 определяются по итерационному правилу:  (26.4)где y(.) – канал измерений ( ), H – матрица канал измерений, I – единичная матрица соответствующей размерности,  - матрица ковариаций начального вектора состояния.Не все компоненты вектора состояний могут быть измерены. Некоторые их них измеряются с некоторой погрешностью, поэтому оценим значения вектора состояний фильтром Калмана. Для этого воспользуемся каналом измерений. 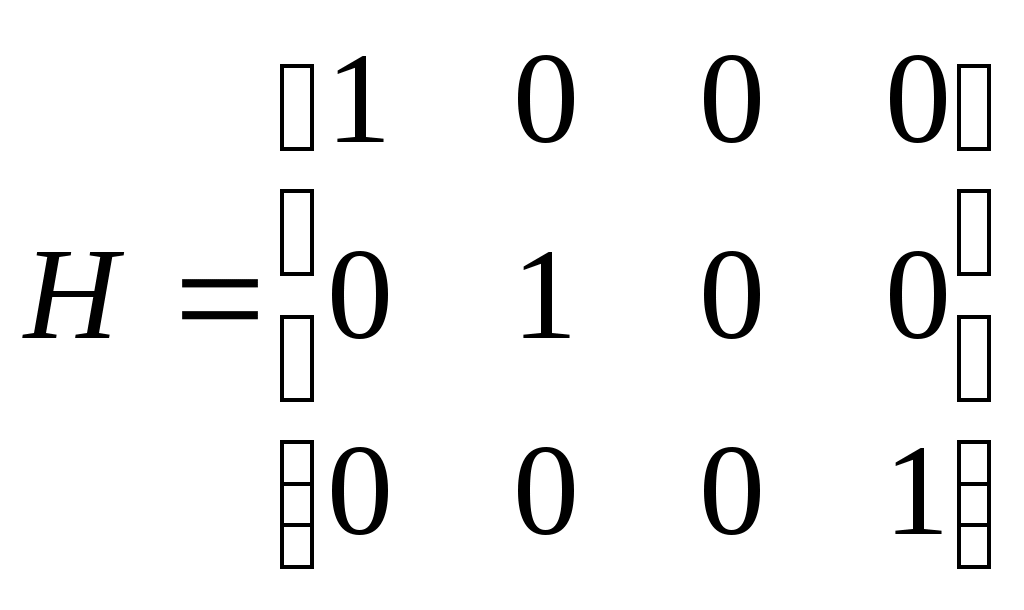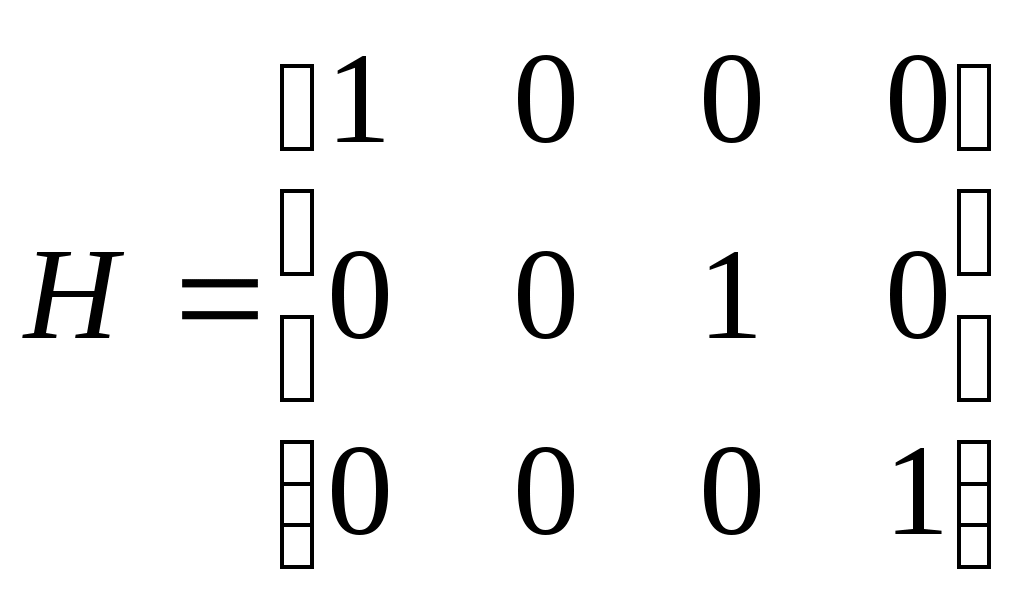H- матрица вида:  , если 2-я компонента вектора состояния - неизмеряемая величина;  , если 1-я компонента вектора состояния - неизмеряемая величина; величина;  , если 1-я и 2-я компоненты вектора состояния – неизмеряемы.В результате оценки вектора состояний фильтром Калмана получим, что оценка практически полностью совпадает со значениями вектора состояний полученными в результате моделирования. Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с. Современные методы идентификации систем. Под ред. П. Эйкгоффа, М.: Мир, 1983. Дополнительная литература Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с. Гроп Д. Методы идентификации систем. - М.: Мир, 1979 |