Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
 Скачать 4.07 Mb.
|
Лекция 24 Параметрическая статистическая идентификация (часть 3)Корреляционные методы идентификации Метод корреляционного анализа используется для идентификации объектов управления в том случае, если входные и выходные сигналы являются случайными величинами. Рассмотрим пример определения АФЧХ на основе АКФ и ВКФ.  Рисунок 24.1 - Схема исследования объекта корреляционным методом При корреляционном анализе используются описанные нами выше: автокорреляционная функция (АКФ) и взаимокорреляционная функция (ВКФ). Напомним, что АКФ характеризует зависимость последующих значений случайной величины от предыдущих, находящихся на расстоянии . 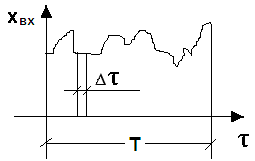 Рисунок 24.2 -. График изменения входной случайной величины – входного сигнала. АКФ:  . При 0 – точнее.Взаимокорреляционная функция связывает две величины, отстоящие друг от друга на . ВКФ:  .С АКФ и ВКФ связаны (через преобразование Фурье, когда входной-выходной сигнал раскладывается в ряд Фурье, состоящий из суммы синусоидальных колебаний с различной – ряд гармоник) спектральные плотности случайных величин.  – для АКФ – для ВКФ.Физически  показывает, какая доля мощности случайной величины приходится на данную частоту.Через спектральную плотность находим искомую АФЧХ объекта: 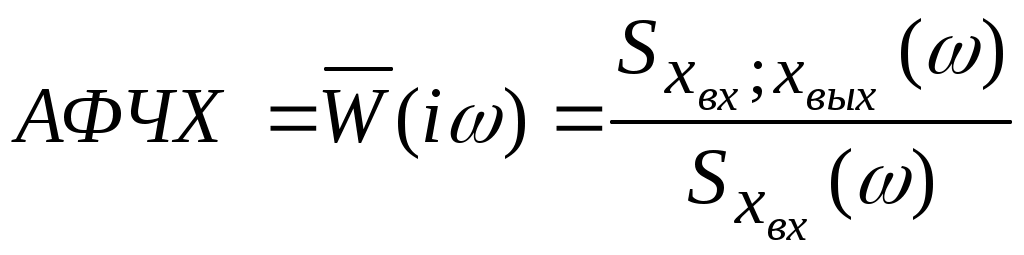 .Однако прежде чем переходить к изложению особенностей различных методов идентификации динамики, необходимо уточнить понятие идентифицируемости объекта. Объект управления следует считать идентифицируемым, если существует вводящаяся за конечное число шагов процедура вычисления его характеристических параметров. Достаточным условием идентифицируемости является наблюдаемость системы. Наблюдаемость (по Калману) — это свойство динамической системы, позволяющее вычислять любой параметр состояния объекта после конечного числа наблюдений. Необходимые условия идентифицируемости отличаются от условий наблюдаемости, т.е. идентифицируемым может оказаться объект и в не полностью наблюдаемой системе. Далее мы рассмотрим математическое обоснование наблюдаемости и идентифицируемости для детерминированных и стохастических систем. В основе статистических методов определения импульсной переходной функции объекта лежит интегральным уравнением Фредгольма  или интегральное уравнение Винера-Хопфа (t>0): , (24.1)где  - импульсная характеристика объекта, весовая функция.Определенная из этого уравнения  является наилучшей в смысле среднеквадратичной оценки. В уравнении (24.1) обозначено Rxy - взаимная корреляционная функция выхода и входа; Rxx - корреляционная функция входного сигнала.Решение уравнения (24.1) с целью определения проводят различными методами, например: методом подбора ординат импульсной функции на управляемом фильтре (требует специальную аппаратуру); методом сведения уравнения (24.1) к системе линейных алгебраических уравнений (см. ниже); методом преобразования Фурье.Стохастическая аппроксимация (СА) (от греч. stochastikos - умеющий угадывать, проницательный и лат. approximo - приближаюсь), метод решения широкого класса задач статистического оценивания, при котором каждое следующее значение оценки получается в виде основанной лишь на новом наблюдении поправки к уже построенной оценке. Основными чертами, обусловившими популярность СА в теоретических и прикладных работах, явились её непараметричность (применимость при весьма скудной информации об объекте наблюдения) и рекуррентность (простота пересчёта оценки при поступлении нового результата наблюдений). СА применяется во многих прикладных задачах теории управления, обучения, в задачах техники, биологии, медицины. СА описана в 1951 американскими статистиками Г. Роббинсом и С. Монро, которые предложили рекуррентный план отыскания корня уравнения регрессии, т. е. корня q уравнения r (x) = a в ситуации, когда каждое измеренное значение ук функции R (x) в точке Xk содержит случайную ошибку. Процедура Роббинса - Монро даётся формулой xK+i = Xk +ак(ук - a). При некоторых условиях на функцию R (x), последовательность ak, стремящуюся к нулю, и на характер случайных ошибок доказано, что Xk ®¥ при увеличении к. Позже метод СА был применен и для решения др. задач: отыскания максимума функции регрессии, оценки неизвестных параметров распределения по наблюдениям и др. На основе изучения предельного распределения нормированной разности xk - q построены асимптотически наилучшие процедуры СА, в которых последовательность ак нужно выбирать зависящей от наблюдений. Основная литература Современные методы идентификации систем. Под ред. П. Эйкгоффа, М.: Мир, 1983 Гроп Д. Методы идентификации систем. – М: Мир, 1979. – 302 с. Дополнительная литература Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с. |