Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление

• Название: Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
• Дата: 24.01.2023
• Размер: 4.07 Mb.
• Имя файла: Лекц комплекс СМИОСУ 2017.doc
• Тип: Конспект лекций; #902228
• страница: 18 из 29

Тема 4 Параметрическая статистическая идентификация

Лекция 21 Основные характеристики времянных рядов

Подробнее (см. [1-4]). Основные понятия: случайная величина и случайный процесс (СП), времянной ряд (ВР), реализация, ансамбль, стационарный СП, эргодический СП, оценка. У стационарных СП матожидание и дисперсия постоянны.

Временной ряд (или ряд динамики) — это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем, элементов) временного ряда.

В то же время выборка — это множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.

Анализ временных рядов — это совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры времянного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.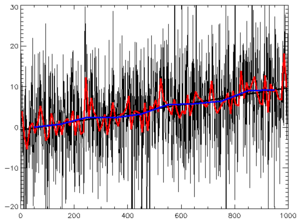



Рисунок 21.1 - Пример временного ряда
Временные ряды состоят из двух элементов:

• 
  периода времени, за который или по состоянию на который приводятся числовые значения;
  
• 
  числовых значений того или иного показателя, называемых уровнями ряда.
  

Временные ряды классифицируются по следующим признакам:

• 
  по форме представления уровней:
  
  • 
    ряды абсолютных показателей;
    
  • 
    относительных показателей;
    
  • 
    средних величин.
    
• 
  по количеству показателей, для который определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
  
• 
  по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
  
• 
  по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
  
• 
  по наличию пропущенных значений: полные и неполные временные ряды;
  
• 
  временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины.
  
• 
  в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
  

Примеры временных рядов (см. рисунок 7.1). Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).

Основной чертой, выделяющей анализ временных рядов среди других видов статистического анализа, является существенность порядка, в котором производятся наблюдения. Если во многих задачах наблюдения статистически независимы, то во временных рядах они, как правило, зависимы, и характер этой зависимости может определяться положением наблюдений в последовательности. Природа ряда и структура порождающего ряд процесса могут предопределять порядок образования последовательности.

Иногда нестационарный СП можно сделать стационарным , удалив низкочастотную аддитивную составляющую (тренд, дрейф), например, применив фильтр верхних частот, использующий спектральное окно Тьюки:

,

где , (21.1)

частота среза fc фильтра связана с его порядком m и частотой изменения времянного ряда .

(матожидание, МО) ВР можно определить как:.

,

Оценка МО (21.2).

(Среднее по N измерениям, выборочное среднее, характеризует постоянное смещение ВР, неслучайная величина, для стационарного СП ).

В условиях АСУТП обычно стоит задача определения МО в режиме реального времени (online). Для этого может быть применена рекуррентная формула:

, (21.3)

где текущее значение МО, - МО определенное на предыдущем шаге, текущее значение x (сигнал от датчика).

Другой вид формулы , где 0<α<2.

Дисперсия ВР представляет собой МО квадрата отклонения x(t) от его среднего.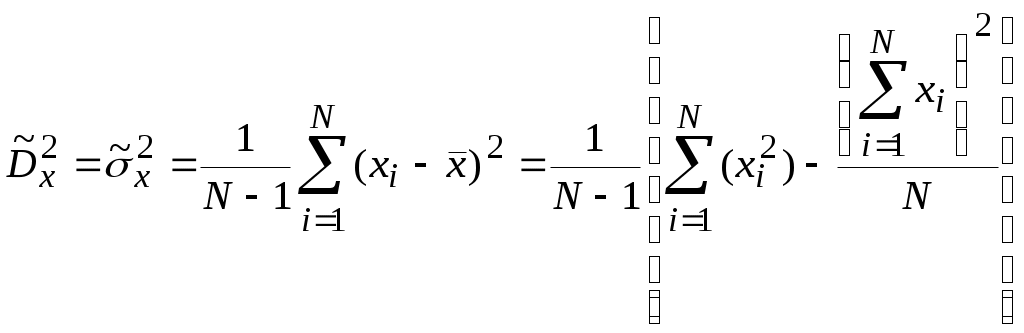

, (21.4)

вторая из формул не требует предварительного определения . Формула (21.4) – выборочная несмещенная дисперсия, если N-1 заменить на N получаем формулу для смещенной дисперсии, при больших N это одно и то же. Иногда дисперсию выражают в процентах. - среднеквадратичная погрешность (формула Бесселя).

В АСУТП в режиме on line дисперсия может быть вычислена по рекуррентном формулам:

(21.5)

Автокорреляционная функция (АКФ) (см. рисунок 21.2а)

АКФ указывает степень связи последующих значений x(t) с предыдущими; определяет вероятность того, что функция x(t), имеющая в момент t значение x1 , будет в момент t+τ значение x2.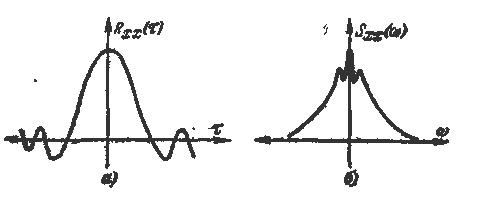

, (21.6)

где , - центрированный ВР; l – смещение (лаг) на l шагов. В реальных процессах вероятность связи между xi и xi+l уменьшается, и Rxx имеет вид, показанный на рисунке 21.2. АКФ является четной функцией, чем круче опускается ее график, тем слабее связь между x(t) и x(t+τ) и наоборот; у белого шума АКФ δ-функция; Rxx = , при l=0.



Рисунок 21.2- Графики автокорреляционной функции (а) и спектральной плотности (б).
Взаимная корреляционная функция (ВКФ)

ВКФ указывает степень связи значений входа x(t) в момент времени t со значениями выхода y(t-τ) в момент времени t-τ.

, (21.7)

функция нечетная, график ее подобен графику АКФ, но смещен вправо на время запаздывания в объекте.

Спектральная плотность (СП)

Представляет собой преобразование Фурье от АКФ, может быть получена из АКФ или математической обработкой реализации СП, показывает, какая доля мощности СП приходится на данную частоту, позволяет судить о частотных свойствах объекта. Типичный график показан на рисунке 21.2.б. Часто получают аналитически, предварительно аппроксимировав каким-либо выражением.

(21.8)

(21.9)

Аналогично записываются выражения и для взаимной спектральной плотности .

При идентификации используют выражения:

(21.10)

(21.11)

Если у процесса имеет одно и то же значение во всем диапазоне частот от -∞ до ∞ то это идеализированный СП, называемый белым шумом (БШ), у которого любое последующее значение x(t) не связано с предыдущими x(t). Для БШ , где - дельта-функция. Часто вместо БШ используют СП без постоянной и без периодической составляющей со статистическими характеристиками:

и . (21.12)

Получение графиков АКФ и ВКФ не представляют особого труда. Однако для расчетов при идентификации обычно используют аналитические выражения. Помимо использования аппроксимации полиномами Чебышева, на практике применяют аппроксимация АКФ показательными и другими функциями.

1). (21.13) (см. рисунке 7.2 ), где α = const, параметр затухания и - дисперсия, получают из аппроксимацией графика. Аналитическое выражение для спектральной плотности получаем в виде:

. (21.14).

В зависимости от вида графика корреляционной функции R_uu (ф )(Рисунок 21.3), ее аппроксимируют одним из следующих выражений.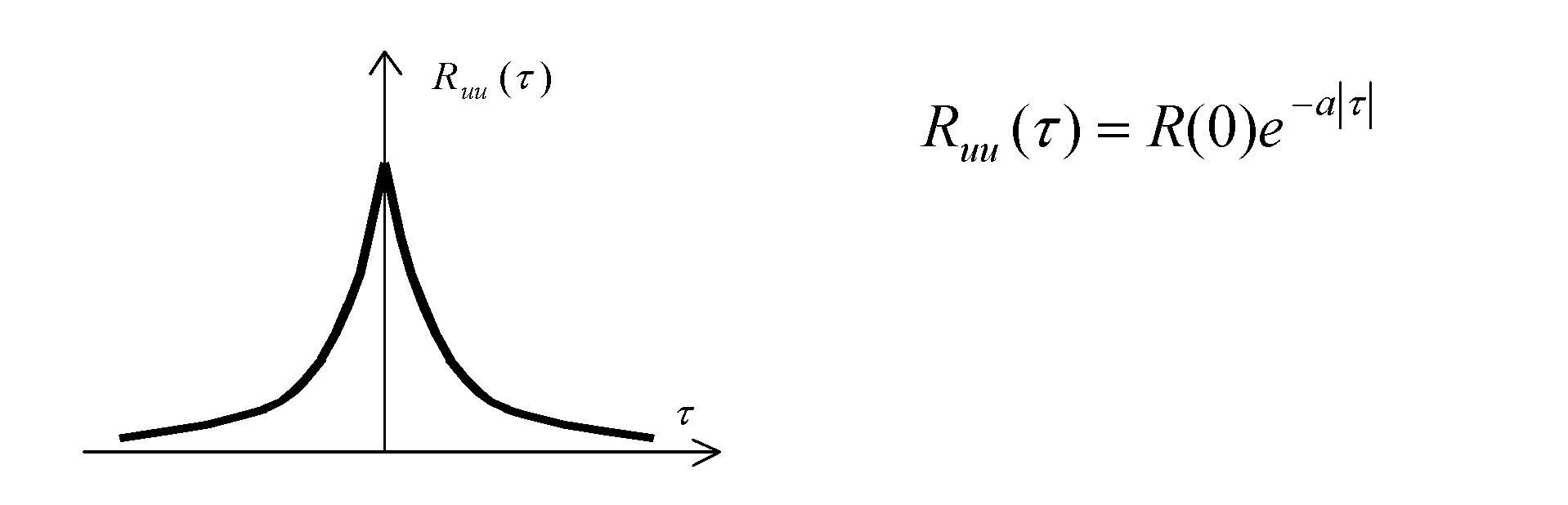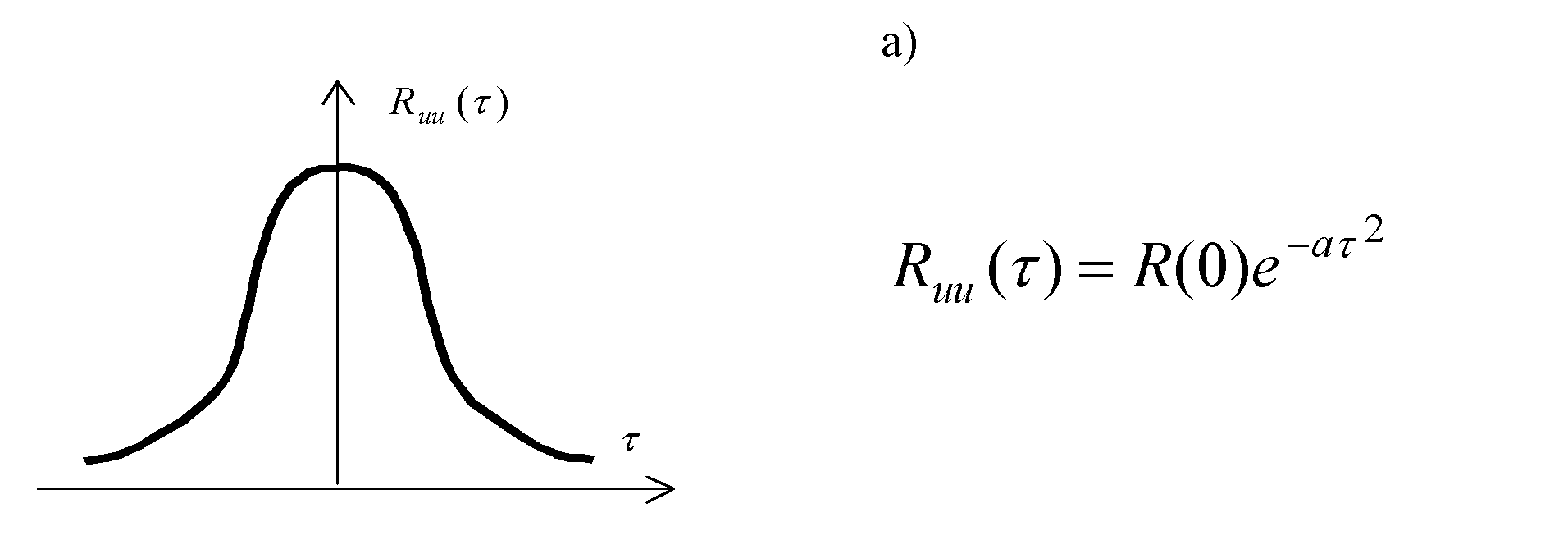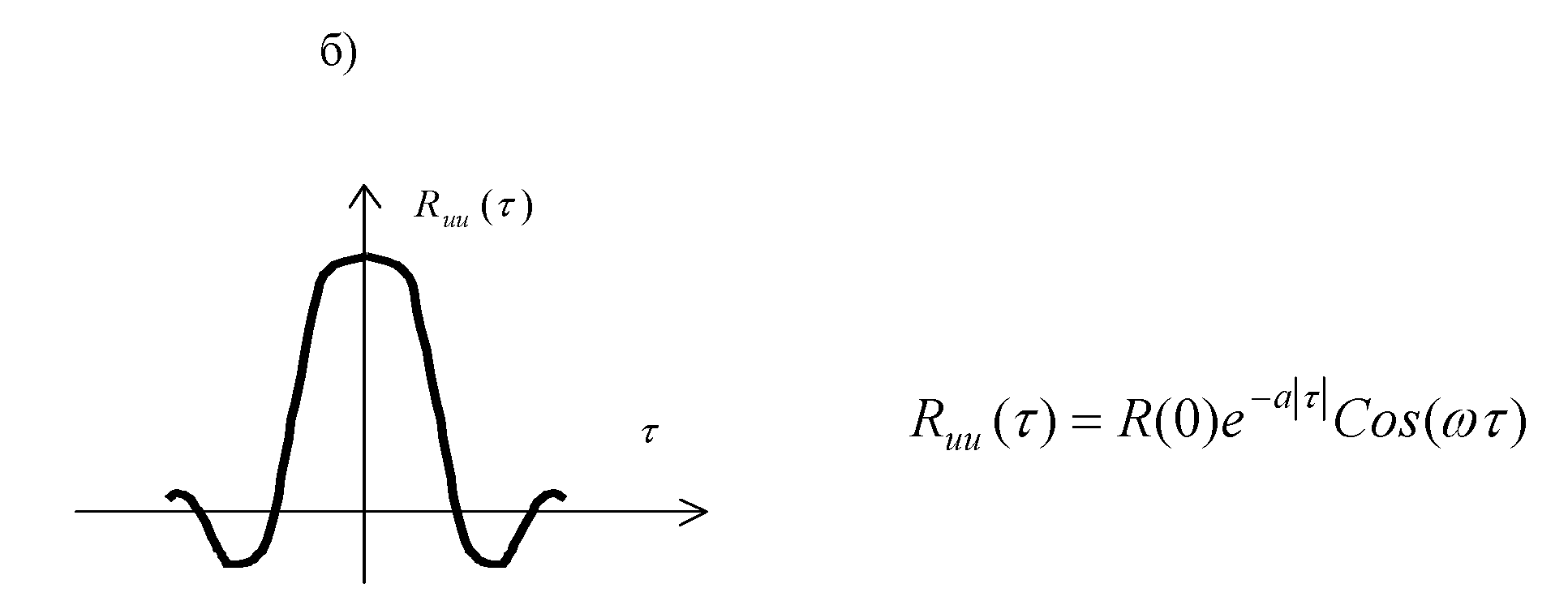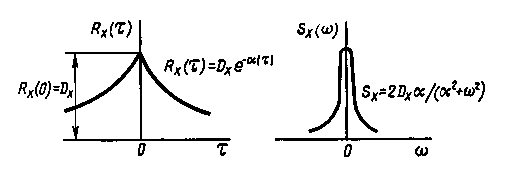








Рисунок 21.3 – аппроксимация АФХ и СП
2). (21.15)

(см. рисунке2.2 ), где ω0 = const - резонансная частота, откуда:

(21.16)

3). (21.17)

Доказывается, что любая АКФ может быть с любой степенью точности описана линейной комбинацией уравнений (21.15, 2.16, 2.17).

Основная литература

1. 
   Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с.
   
2. 
   Исмаилов С.У. Современные методы идентификации объектов и систем управления. Методические указания к выполнению лабораторных работ для магистрантов спец. 6М0702. Шымкент, ЮКГУ, 2010 г., -78 с.
   

Дополнительная литература

3. 
   Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М. Масленникова. -М.: Химия, 1986. -336с.
   
4. 
   Гроп Д. Методы идентификации систем. - М.: Мир, 1979