Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление

• Название: Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
• Дата: 24.01.2023
• Размер: 4.07 Mb.
• Имя файла: Лекц комплекс СМИОСУ 2017.doc
• Тип: Конспект лекций; #902228
• страница: 19 из 29

Лекция 22 Параметрическая статистическая идентификация (часть 1)

Структурная и параметрическая идентификация. Моделирование (в широком смысле) является основным методом исследований во всех областях знаний и научно обоснованным методом оценок характеристик сложных систем, используемым для принятия решений в различных сферах инженерной деятельности. Существующие и проектируемые системы можно эффективно исследовать с помощью математических моделей (аналитических и имитационных), реализуемых на современных ЭВМ, которые в этом случае выступают в качестве инструмента экспериментатора с моделью системы.

Одна из проблем современной науки и техники — разработка и внедрение в практику проектирования новейших методов исследования характеристик сложных информационно-управляющих и информационно-вычислительных систем различных уровней (например, автоматизированных систем научных исследований и комплексных испытаний, систем автоматизации проектирования, АСУ технологическими процессами, а также интегрированных АСУ, вычислительных систем, комплексов и сетей, информационных систем, цифровых сетей интегрального обслуживания и т. д.). При проектировании сложных систем и их подсистем возникают многочисленные задачи, требующие оценки количественных и качественных закономерностей процессов функционирования такихсистем, проведения структурного алгоритмического и параметрического их синтеза.

Характеризуя проблему моделирования в целом, необходимо учитывать, что от постановки задачи моделирования до интерпретации полученных результатов существует большая группа сложных научно-технических проблем, к основным из которых можно отнести следующие: идентификацию реальных объектов, выбор вида моделей, построение моделей и их машинную реализацию, взаимодействие исследователя с моделью в ходе машинного эксперимента, проверку правильности полученных в ходе моделирования результатов, выявление основных закономерностей, исследованных в процессе моделирования. В зависимости от объекта моделирования и вида используемой модели эти проблемы могут иметь разную значимость.

В одних случаях наиболее сложной оказывается идентификация, в других — проблема построения формальной структуры объекта. Возможны трудности и при реализации модели, особенно в случае имитационного моделирования больших систем. При этом следует подчеркнуть роль исследователя в процессе моделирования. Постановка задачи, построение содержательной модели реального объекта во многом представляют собой творческий процесс и базируются на эвристике. И в этом смысле нет формальных путей выбора оптимального вида модели. Часто отсутствуют формальные методы, позволяющие достаточно точно описать реальный процесс. Поэтому выбор той или иной аналогии, выбор того или иного математического аппарата моделирования полностью основывается на имеющемся опыте исследователя и ошибка исследователя может привести к ошибочным результатам моделирования.

Идентификацией называется нахождение оптимальной в некотором смысле модели Аm (или оценки оператора) объекта являющейся функцией входных (U) и выходных (Y или X) параметров системы, построенной по результатам наблюдений над входными и выходными переменными объекта.

Полученная модель, (в случае ее адекватности исследуемому объекту) в основном, предназначена для замены реального объекта в задачах управления, прогноза, конструирования, поиска оптимальных режимов и условий, имитации явлений и устройств и т.п.

Задачей идентификации называется обратная задача системного синтеза.

Среди задач идентификации выделяют два типа (проблемы):

структурная идентификация (в широком смысле слова);

параметрическая идентификация (идентификация в узком смысле слова).

Структурная идентификация подразумевает построение модели типа «черный ящик», т.е. информация об объекте отсутствует полностью или частично. Главная задача структурной идентификации - определение структуры модели (см. рисунок 22.1).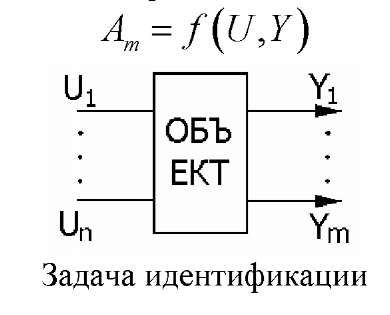


Рисунок 22.1 – Задача идентификации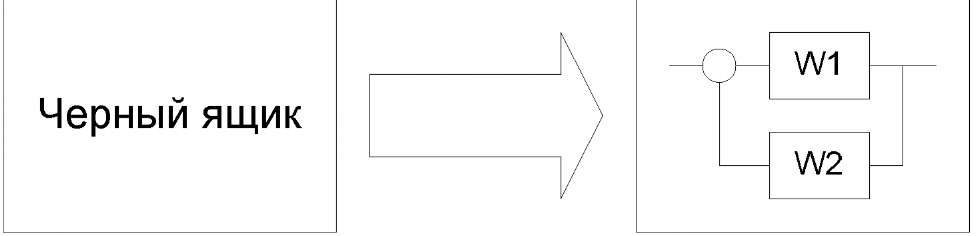


Рисунок 22.2- Структурная идентификация
Первая проблема - структурная идентификация является, по существу, основной проблемой всего процесса моделирования, состоящего из следующих четырех основных этапов:

• 
  постановка задачи
  
• 
  выбор структуры модели и математическое описание ее блоков;
  
• 
  исследование модели;
  
• 
  экспериментальная проверка модели.
  

Структура модели ещё не сама модель, и для определения ее параметров необходимо располагать измерениями. Задачу определения параметров модели по наблюдениям работы объекта при заданной структуре модели называют идентификацией в узком смысле или параметрической идентификацией. Например, известна система уравнений, описывающая некоторый объект. Необходимо определить только коэффициенты уравнений. Процедура структурной идентификации показана на рисунке 22.3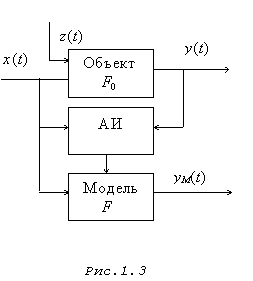



АИ – алгоритм идентификации

Рисунок 22.3 – Процедура идентификации

Вторая проблема (параметрическая идентификация) при заданной структуре модели поддается формализации и смыкается с четвертым этапом моделировании.

Таким образом, по отношению к многоэтапному процессу моделирования в целом идентификация выступает как инструмент проверки гипотез о соответствии структуры или параметров объекта и модели на основе экспериментальных данных о его функционировании. Характер и степень несоответствия используются при этом для принятия содержательных или формализованных решений по корректировке модели (см. рисунки 22.4 и 22.5)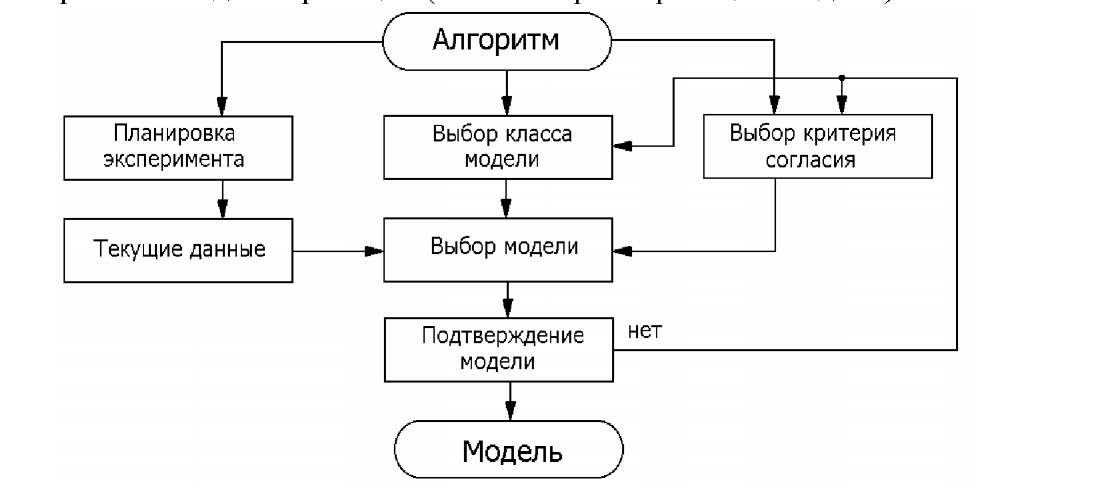



Рисунок 22.4 - Общая схема идентификации модели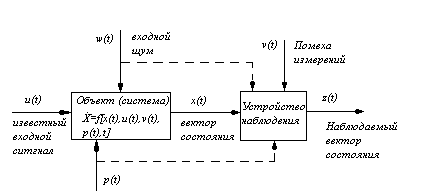



Рисунок 22.5 - Структурная схема идентификации модели
На этом рисунке - текущие данные могут быть получены в результате пассивного или активного эксперимента. Пассивный эксперимент, когда исследователь не влияет на процедуру регистрации (изменения) данных. Активный эксперимент, когда исследователь формирует программу эксперимента.

Методы планирования эксперимента позволяют эффективно организовать эксперимент. Выбор класса модели и модели – достаточно сложная процедура при решении которых обычно приходится делать компромиссный выбор между сложностью модели и её точностью. Выбор критерия согласия - это выбор критерия точности математического описания. Часто используют для этого метод наименьших квадратов. Метод наименьших квадратов не требует никакой априорной информации. В отдельных практических задачах автоматического управления в качестве мер сравнения можно принимать различные характеристики (временные, частотные и т.д.) объекта и модели. Критерием идентификации в этом случае является рассогласование этих характеристик. Однако, если модель используется в самонастраивающейся САУ, настройка модели по динамическим характеристикам требует наличие измерителей динамических характеристик объекта и модели, что приводит к конструктивному усложнению САУ и уменьшению быстродействия контуров самонастройки.

Построение моделей опирается в основном на данные наблюдений. Существует два способа (а также комбинации) формирования математических моделей.

В первом способе исследуемая система расчленяется на такие подсистемы, свойства которых очевидны из ранее накопленного опыта. По существу, это означает, что мы опираемся на известные законы природы и другие надежные соотношения, основанные на ранее проведенных экспериментальных исследованиях. Формальное математическое объединение этих подсистем становится моделью всей системы. Такой подход называется моделированием или аналитическим методом построения моделей. В его рамках проведение натурного эксперимента не обязательно. Конкретный вид процедуры моделирования сильно зависит от прикладной задачи и часто определяется традиционными и специфическими средствами из рассматриваемой прикладной области. Основной прием сводится к структуризации процесса в виде блок-схемы, блоки которой состоят из более простых элементов. Процесс восстановления системы по этим простым блокам чаще всего выполняется с помощью ЭВМ и приводит не к математической, а к машинной модели системы.

В другом способе построения моделей непосредственно используются экспериментальные данные. В этом случае ведётся регистрация входных и выходных сигналов системы, и модель формируется в результате обработки соответствующих данных. Этот способ называется идентификацией.
Идентификация на основе методов оценивания

Байесовские оценки. Теорема выражается т. н. формулой Байеса:

(22.1)

где

P(A) — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

P(A | B) — вероятность гипотезы A при наступлении события B (апостериорная вероятность);

P(B | A) — вероятность наступления события B при истинности гипотезы A;

P(B) — вероятность наступления события B.

Вывод формулы. Формула элементарно выводится из определения условной вероятности:



Физический смысл и терминология. Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. События, отражающие действие «причин», в данном случае обычно называют «гипотезами», так как они — предполагаемые события, повлекшие данное. Также, безусловную вероятность справедливости «гипотезы» называют «априорной» (насколько вероятна причина вообще), а условную при произошедшем событии — «апостериорной» (насколько вероятна причина оказалась с учетом полученных данных о событии).

Важным следствием формулы Байеса является формула полной вероятности события, зависящего от нескольких несовместных гипотез (и только от них!).

— вероятность наступления события B, зависящего от ряда гипотез A_i, если известны степени достоверности этих гипотез (например, измерены экспериментально);

Вывод теоремы. Если событие зависит только от причин A_i, то если оно произошло, значит, обязательно произошла какая-то из причин, т.е.



По формуле Байеса



Переносом P(B) вправо получаем искомое выражение.

Пример использования метода Байеса для фильтрации спама в электронной почте. Метод, основанный на теореме Байеса, нашел успешное применение в фильтрации спама. При обучении фильтра для каждого встреченного в письмах слова высчитывается и сохраняется его «вес» — вероятность того, что письмо с этим словом — спам (в простейшем случае — по классическому определению вероятности: «появлений в спаме / появлений всего»).

При проверке вновь пришедшего письма вычисляется вероятность того, что оно — спам, по указанной выше формуле для множества гипотез. В данном случае «гипотезы» — это слова, и для каждого слова «достоверность гипотезы» — % этого слова в письме, а «зависимость события от гипотезы» P(B | A_i) — вычисленный ранее «вес» слова. То есть «вес» письма в данном случае — не что иное, как усредненный «вес» всех его слов. Отнесение письма к «спаму» или «не-спаму» производится по тому, превышает ли его «вес» некую планку, заданную пользователем (обычно берут 60-80 %). После принятия решения по письму в базе данных обновляются «веса» для вошедших в него слов.

Данный метод прост (алгоритмы элементарны), удобен (позволяет обходиться без «черных списков» и подобных искусственных приемов), эффективен (после обучения на достаточно большой выборке отсекает до 95—97 % спама, и в случае любых ошибок его можно дообучать). В общем, есть все показания для его повсеместного использования, что и имеет место на практике — на его основе построены практически все современные спам-фильтры.

Впрочем, у метода есть и принципиальный недостаток: он базируется на предположении, что одни слова чаще встречаются в спаме, а другие — в обычных письмах, и неэффективен, если данное предположение неверно. Впрочем, как показывает практика, такой спам даже человек не в состоянии определить «на глаз» — только прочтя письмо и поняв его смысл.

Еще один, не принципиальный, недостаток, связанный с реализацией — метод работает только с текстом. Зная об этом ограничении, спамеры стали вкладывать рекламную информацию в картинку, текст же в письме либо отсутствует, либо не несет смысла. Против этого приходится пользоваться либо средствами распознавания текста («дорогая» процедура, применяется только при крайней необходимости), либо старыми методами фильтрации — «черные списки» и регулярные выражения (так как такие письма часто имеют стереотипную форму).

Общие задачи статистической идентификации. В практике моделирования систем наиболее часто приходится иметь дело с объектами, которые в процессе своего функционирования содержат элементы стохастичности или подвергаются стохастическим воздействиям вне­шней среды. Поэтому основным методом получения результатов с помощью имитационных моделей таких стохастических систем является метод стати­стического моделирования на ЭВМ, использующий в качестве теоретической базы предельные теоремы теории вероятностей. Возможность получения пользователем модели результатов статистического моделирования сложных систем в условиях ограниченности машинных ресурсов существенно зависит от эффективности процедур генерации псевдослучайных последовательностей на ЭВМ, положенных в основу имитации воздействий на элементы моде­лируемой системы.

Общая характеристика метода статистического моделирования. На этапе исследования и проектирования систем при построении и реализации машинных моделей (аналитических и имитационных) широко используется метод статистических испытаний (Монте-Кар­ло), который базируется на использовании случайных чисел, т. е. возможных значений некоторой случайной величины с заданным распределением вероятностей. Статистическое моделирование пред­ставляет собой метод получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемой системе. Для получения представляющих интерес оценок характеристик моделируемой системы S с учетом воздействий внешней сре­ды Е статистические данные обрабатываются и классифицируют­ся с использованием методов математической статистики.

Сущность метода статистического моделирования. Таким образом, сущность метода статистического моделирования сводится к построению для процесса функционирования исследуемой систе­мы S некоторого моделирующего алгоритма, имитирующего пове­дение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды Е, и реализации этого алгоритма с использованием программно-технических средств ЭВМ.

Различают две области применения метода статистического мо­делирования:

1) для изучения стохастических систем;

2) для решения детерминированных задач.

Основной идеей, которая используется для решения детерминированных задач методом статистического моделирования, является замена детерминированной задачи эквива­лентной схемой некоторой стохастической системы, выходные хара­ктеристики последней совпадают с результатом решения детерми­нированной задачи. Естественно, что при такой замене вместо точного решения задачи получается приближенное решение и погре­шность уменьшается с увеличением числа испытаний (реализации моделирующего алгоритма) N.

В результате статистического моделирования системы S получа­ется серия частных значений искомых величин или функций, стати­стическая обработка которых позволяет получить сведения о пове­дении реального объекта или процесса в произвольные моменты времени. Если количество реализации N достаточно велико, то полученные результаты моделирования системы приобретают статистическую устойчивость и с достаточной точностью могут быть приняты в качестве оценок искомых характеристик процесса функ­ционирования системы S.

Теоретической основой метода статистического моделирования систем на ЭВМ являются предельные теоремы теории вероятностей. Множества случайных явлений (событий, величин) подчиняются определенным закономерностям, позволя­ющим не только прогнозировать их поведение, но и количественно оценить некото­рые средние их характеристики, проявляющие определенную устойчивость. Харак­терные закономерности наблюдаются также в распределениях случайных величин, которые образуются при сложении множества воздействий. Выражением этих зако­номерностей и устойчивости средних показателей являются так называемые предель­ные теоремы теории вероятностей, часть из которых приводится ниже в пригодной для практического использования при статистическом моделировании формулиров­ке. Принципиальное значение предельных теорем состоит в том, что они гарантиру­ют высокое качество статистических оценок при весьма большом числе испытаний (реализации) N. Практически приемлемые при статистическом моделировании коли­чественные оценки характеристик систем часто могут быть получены уже при сравнительно небольших (при использовании ЭВМ) N.

Основная литература

1. 
   Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с.
   
2. 
   Исмаилов С.У. Современные методы идентификации объектов и систем управления. Методические указания к выполнению лабораторных работ для магистрантов спец. 6М0702. Шымкент, ЮКГУ, 2010 г., -78 с.
   

Дополнительная литература

3. 
   Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М. Масленникова. -М.: Химия, 1986. -336с.
   
4. 
   Гроп Д. Методы идентификации систем. - М.: Мир, 1979