Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
 Скачать 4.07 Mb. Скачать 4.07 Mb.
|
Лекция 23 Параметрическая статистическая идентификация (часть 2)Общая схема процесса идентификации Рассмотрим перечень примерных этапов идентификации. Технология математического моделирования технических систем в общем случае предполагает выполнение следующих основных этапов: Формулировка целей. В основе всякой задачи, проблемы моделирования лежит информация о том, какие зависимости нас интересуют, каковы его цели его использования. Именно эта информация определяет объект. Эти представления могут быть очень приближенными, но всегда отражают некоторые его свойства, достаточные для эффективной формулировки целей моделирования. Обычно в задачах моделирования цель достигается путем максимизации или минимизации некоторого критерия, задаваемого в виде целевой функции. Изучение объекта. При этом требуется понять происходящий процесс, определить границы объекта с окружающей его средой, если таковые имеются. Кроме того, на данном этапе определяются перечень всех входных и выходных параметров объекта исследования и их влияние на достижение целей моделирования. Описательное моделирование (разработка концептуальной модели) - установление и словесная фиксация основных связей входных и выходных параметров объекта. Математическое моделирование (разработка математической модели)- перевод описательной модели на формальный математический язык. Цель записывается в виде функции, которую обычно называют целевой. Поведение объекта описывается с помощью соотношений, входные и выходные параметры объекта на данном этапе в зависимости от сложности исследуемой проблемы могут возникать ряд задач чисто математического характера. Такими задачами являются задачи математического программирования, линейной алгебры, задачи дифференциального и интегрального исчисления и многие другие. Выбор (или создание) метода решения задачи. На данном этапе для возникшей математической задачи подберется подходящий метод. При выборе такого метода необходимо будет обратить внимание на сложность метода и потребляемые вычислительные ресурсы. Если подходящего метода по предъявленным критериям не окажется, то требуется разработать новый метод решения задачи. Мы делаем упор на разработку новых эффективных методов, не уступающих известным методам по основным вычислительным характеристикам. Выбор или написание компьютерных программы. На данном этапе выбирается подходящая программа, реализующая выбранный метод решения. Если такая программа отсутствует, то необходимо написать такую программу. Решение задачи на компьютере. Вся необходимая информация для решения задачи вводится в память компьютера вместе с программой. С использованием подходящей программы производится обработка целевой информации и получение результатов решения задач в удобной форме. Проверка адекватности модели (верификация модели). Анализ получаемого решения. Анализ решения бывают двух видов: формальный (математический), когда проверяется соответствие полученного решения построенной математической модели (в случае несоответствия проверяется программа, исходные данные, работа ЭВМ и др.) и содержательный (экономический, технологический и т.п.), когда проверяется соотв 0 етствие полученного решения тому объекту, который моделировался. В результате такого анализа в модель могут быть внесены изменения или уточнения, после чего весь рассмотренный процесс повторяется. Модель считается построенной и завершенной, если она с достаточной точностью характеризует деятельность объекта по выбранному критерию. Только после этого модель можно использовать при расчетах. Перечисленные этапы вытекают из общей методологии моделирования систем. При моделировании различных систем трудоемкости одних и тех же этапов могут быть разными. В процессе моделирования конкретной системы могут иметь место некоторые изменения технологии. В частности, может быть заранее предопределен метод моделирования или выбрано конкретное средство моделирования. Математическая модель окажется настолько простой, что не потребуется проведения машинных экспериментов, разработка программной модели исключит необходимость создания математической модели. Следует обратить внимание на первоочередную необходимость постановки, формулирования цели моделирования. В этом вопросе должно быть достигнуто взаимопонимание между заказчиком, ответственным за создание или модернизацию системы, и разработчиком модели. Важность корректного выполнения этого этапа определяется тем, что все последующие этапы проводятся с ориентацией на определенную цель моделирования. На этом же этапе конкретизируется, в каких единицах измерения (относительных или абсолютных) должны быть представлены результаты моделирования. Под относительными единицами здесь понимаются качественные градации, сравнительные оценки разных вариантов системы (типа «лучше—хуже», «больше— меньше»). При необходимости представления результатов в абсолютных единицах должен быть решен вопрос о точности измерения. Этот вопрос зачастую не имеет однозначного ответа, но крайне важен для выполнения всех этапов моделирования. Проверка адекватности указана выше в виде одного из этапов моделирования. Не надо это понимать буквально, так как на адекватность модели оказывает влияние качество выполнения практически всех этапов. Поэтому проверка адекватности должна проводиться в том или ином виде, начиная от разработки концептуальной модели и кончая анализом результатов моделирования. Под разработкой математической модели подразумевается создание полностью формализованного описания динамики функционирования системы. Однако не для всех систем, внешних условий и целей моделирования может быть подобран известный метод формализации или конструктивный математический аппарат. Тем не менее и для таких систем следует разработать однозначные зависимости выходных характеристик от параметров и воздействий для каждой составляющей системы, алгоритмы взаимодействия между составляющими, логические условия изменения состояний. Результаты машинного моделирования должны быть проанализированы с целью проверки их достоверности и выработки рекомендаций о способах повышения качества исследуемой системы. На всех этапах моделирования следует обратить особое внимание на документирование принимаемых решений, допущений, ограничений и выводов. Из организационных аспектов моделирования следует выделить необходимость непосредственного участия в работе квалифицированных представителей заказчика на первых этапах (вплоть до разработки математической модели) и на этапе анализа результатов моделирования. Ответственный за систему заказчик должен четко понимать цели моделирования, разработанную концептуальную модель, программу исследований и полученные результаты. Это будет способствовать внедрению выработанных рекомендаций. Математическое моделирование технических систем предполагает применение следующих методов: аналитических; численных; статистических (имитационных); аналитико-имитационных. Выбор конкретного метода моделирования зависит от многих факторов, в том числе от: целей моделирования; сложности исследуемой системы; сложности модели, определяемой выбранным уровнем ее детализации; требований к номенклатуре исследуемых характеристик; требований к точности получаемых результатов; требований к общности получаемых результатов; требований к затратам времени на моделирование; требований к материальным затратам; наличия специальных технических средств для проведения моделирования; квалификации специалиста, проводящего моделирование и т.д. Результаты сравнительного анализа методов моделирования, выполненного на качественном уровне, представлены в таблице23.1 (фигурными скобками отмечены наилучшие значения каждого показателя). Таблица 23.1 Результаты сравнительного анализа методов моделирования
Для решения задач математического моделирования и идентификации необходима исходная информация. Её условно разделяют на два вида - априорную и апостериорную информацию. (априорная информация [aprior information] и апостериорная информация [aposterior information]). Соответственно, это данные, имевшиеся до проведения какого-либо опыта или другого действия, и сведения, полученные после его выполнения. Обычно приходиться работать в условиях неполноты априорной и текущей информации об объекте и при наличии неконтролируемых возмущений различного происхождения. В том случае, если объект рассматривается как «черный ящик», то как правило используют только апостериорную информацию. «Чёрный ящик» — термин, используемый в точных науках (в частности, системотехнике, кибернетике и др.) для обозначения системы, механизм работы которой очень сложен, неизвестен или неважен в рамках данной задачи. Такие системы обычно имеют некий «вход» для ввода информации и «выход» для отображения результатов работы. Состояние выходов обычно функционально зависит от состояния входов. Использование априорной информации об объекте исследования (если она доступна) во многих случаях облегчает решение проблемы идентификации. Критерии и показатели качества идентификации. Формирование критерия качества, характеризующего адекватность модели реальному объекту, является одним из основных этапов идентификации. Переход от исследования объекта к исследованию модели и подтверждение пригодности модели для решения задач моделирования требует оценку качества полученной модели, т.е. проверку адекватности модели и объекта. Никогда нельзя говорить об абсолютной адекватности, при которой модель по всем свойствам соответствует объекту, так как в зависимости от цели исследования могут строиться различные модели объекта. Например, при исследовании влияния размещения пассажиров на центровку самолета моделью человека может служить мешок с песком, для конструктора одежды - манекен, а для медико-биологических исследований - животные. Таким образом, всякая модель имеет характер проекции и отражает отдельные свойства объекта. В связи с этим основное подтверждение модели заключается в том, чтобы убедиться в возможности использования полученной модели для решения той задачи, ради которой эта модель и строилась. Поэтому адекватность предполагает воспроизведение моделью с необходимой полнотой всех свойств объекта, существенных для целей данного исследования. Количественно степень адекватности модели и объекта можно оценить путем сравнения их выходных сигналов при подаче одинаковых входных воздействий на объект и его модель. Такое сравнение предпочтительное на основе новой информации, отличной от того множества данных, которое использовалось в процессе идентификации объекта. Структурная схема вычисления оценки ошибки модели статического объекта приведена на рисунке 23.1.  Рисунок 23.1 - Структурная схема вычисления оценки ошибки модели Пусть проведено l опытов при различных уровнях входных воздействий из области их допустимых значений и получены реализации выходов объекта и выходы модели , . Ошибки модели и для оценки ее адекватности вычисляются по формулам: , ; 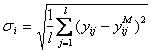 , , , , где - абсолютная, приведенная и среднеквадратичная ошибки модели по i-му выходу ; - значение i-го выхода объекта и модели в j-ом опыте ; - максимальное изменение i-го выхода объекта при допустимых значениях входов из области . Если величины этих ошибок меньше некоторого заданного положительного числа, то модель адекватна объекту. Теперь рассмотрим оценку модели динамического объекта. Положим, что после идентификации получена модель одномерного объекта в форме линейного дифференциального уравнения вида. где - входной сигнал модели; - выходной сигнал модели; n,m - наивысшие порядки производных; и соответственно . Пусть получены реализации входа и выхода объекта на отрезке времени , где - длина реализации (время наблюдения). Теперь качество модели можно оценить путем сравнения и либо непосредственно на графике (визуально),либо введя некоторую формальную меру расстояния между этими сигналами. Выходные сигналы объекта и модели при одном и том же входном сигнале различаются, так как их дифференциальные уравнения и начальные состояния неидентичны. Для оценки адекватности модели и объекта введем критерий их близости по разности выходных сигналов, т.е. реакций на один и тот же входной сигнал , например следующего вида: 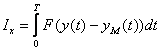 , (23.2) , (23.2) где - некоторая выпуклая функция. В частности: . (23.3) В общем случае оценка адекватности проводится для различных форм входного сигнала . Отсюда следует идея необходимости усреднения по входным сигналам и начальным условиям, т.е. введения операции математического ожидания оценки : 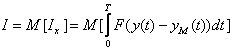 . (23.4) . (23.4)Выражение выходного сигнала имеет довольно сложный вид, что затрудняет аналитическое исследование зависимости от коэффициентов модели, поэтому вводятся и другие критерии. В частности, если уравнение модели имеет вид то для оценки близости модели и объекта удобным оказывается функционал от разности входных сигналов модели и объекта, обеспечивающих один и тот же выходной сигнал: 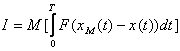 , (23.6) , (23.6) при условии, что . В этом случае выходной сигнал модели и объекта будем обозначать . Тогда, подставляя (23.5) в (23.6), имеем 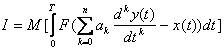 , (23.7) , (23.7)т.е. функционал в явном виде зависит от коэффициентов модели, что удобно для аналитического исследования. Развивая эту идею, можно формализовать удобный функционал для общего случая модели (23.1) 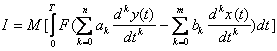 . (23.8) . (23.8) Выражение: называется обобщенной ошибкой модели. В качестве функции , как правило, принимают квадрат обобщенной ошибки . (23.11) Этот функционал удобен тем, что в явном виде зависит от параметров модели и от доступного измерения входного и выходного сигналов объекта. Однако при вычислении этого функционала возникают определенные трудности, связанные с дифференцированием сигналов и , а также с необходимостью выполнения операции математического ожидания. Структурная схема вычисления обобщенной ошибки и оценки критерия представлена на на рисунке 23.2, где - оператор дифференцирования.  Рисунок 23.2 - Структурная схема вычисления обобщенной ошибки и оценки критерия Однако по условиям физической реализуемости можно создавать лишь устройства, порядок числителя которых меньше (или равно) порядка знаменателя, т.е. можно реализовать устройства с операторами где - многочлен степени больше или равно ; . Тогда структурная схема вычисления обобщенной ошибки и оценки критерия будет иметь вид, представленной на рисунке 23.3.  Рисунок 23.3 - Структурная схема вычисления обобщенной ошибки . (23.13) Структурной схеме, изображенной на рисунке 23.3, эквивалентна схема, приведенная на на рисунке 23.4.  Рисунок 23.4 – Эквивалентная структурная схема вычисления обобщенной ошибки Таким образом, обобщенная ошибка , измеряемая с помощью физически реализуемых устройств, отличается от обобщенной ошибки тем, что является результатом преобразования фильтром с передаточной функцией . В силу конечности полосы пропускания этого фильтра происходят искажения сигнала обобщенной ошибки. Эти искажения будут тем меньше, чем больше полоса пропускания фильтра. Если величина ошибок модели и оценок критериев приближения удовлетворяют требованиям к качеству модели, то модель считается адекватной объекту и может быть использована для решения задач моделирования, оптимизации и управления. В противном случае модель необходимо усовершенствовать путем изменения структуры и введения в нее неучтенных ранее факторов. Основная литература Современные методы идентификации систем. Под ред. П. Эйкгоффа, М.: Мир, 1983 Ордынцев В. М. Математическое описание объектов автоматизации. – М: Машиностроение, 1965. – 360 с. Гроп Д. Методы идентификации систем. – М: Мир, 1979. – 302 с. Дополнительная литература Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с. Семенов А. Д., Артамонов Д. В., Брюхачев А. В. Идентификация объектов управления: Учебн. пособие. - Пенза: Изд-во Пенз. гос. ун-та, 2003.- 211 с. Исмаилов С.У. Современные методы идентификации объектов и систем управления. Методические указания к выполнению лабораторных работ для магистрантов спец. 6М0702. Шымкент, ЮКГУ, 2010 г., -78 с. |
