Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление

• Название: Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
• Дата: 24.01.2023
• Размер: 4.07 Mb.
• Имя файла: Лекц комплекс СМИОСУ 2017.doc
• Тип: Конспект лекций; #902228
• страница: 17 из 29

Лекция 20 Определение переходных характеристик

Определение переходных характеристик. Аппроксимация временных характеристик

Идентификация с помощью переходной функции проводится автономно, вне про­цесса управления, и поэтому применима только к стационарным процессам. Однако поскольку ступенчатые возмущения воздей­ствуют на многие (если не на большинство) системы во время включения или в процессе нормальной работы, то переходные функцщ 'можно записать, не нарушая нормального режима ра­боты системы. B этом заключается дополнительное преимущест­во рассматриваемого метода. Очевидно, при этом необходимо предположить, что система стационарная, так как результаты идентификации считаются достоверными и после приложения ступенчатого сигнала. Кроме того, предполагается, что в диапа­зоне амплитуд ступенчатого сигнала система линейна.

Для получения временной динамической характеристики объекта регулирования организуют специальный эксперимент.

В какой-то момент времени к объекту регулирования, находящемуся в установившемся режиме работы, прикладывают некоторое возмущающее воздействие и затем регистрируют отклонения регулируемой величины во времени до ее восстановившегося значения с помощью соответствующего измерительного прибора.

Перед началом эксперимента нужно убедиться в том, что объект регулирования находится в установившемся режиме работы. Для достоверности измеренных отклонений регулируемой величины необходимо один и тот же опыт повторять 2-3 раза.

В найденную путем эксперимента динамическую характеристику объекта включены характеристика собственно объекта и характеристика регистрирующего прибора.

В связи с этим желательно в качестве датчиков отклонений физических величин от их номинальных значений применять те, которые входят в измерительный блок регулирующего устройства, поддерживающего на каком-то значении данную физическую величину.

Для определения динамических свойств объекта на практике чаще всего используют методику снятия переходной характеристики. При определении динамических характеристик объекта по его переходной характеристике (кривой разгона) на вход подается или ступенчатый пробный сигнал или прямоугольный импульс. Во втором случае переходная характеристика (кривая отклика) должна быть достроена до соответствующей кривой разгона. Процесс получения передаточной функции объекта, исходя из данных о переходном процессе, называется идентификацией объекта.

При снятии переходной характеристики необходимо выполнить ряд условий,
представленных в таблице 20.1:
Таблица 20.1

Условия снятия переходной характеристики

No	Условия
1	Если проектируется система стабилизации технологического параметра, то переходная характеристика должна сниматься в окрестности рабочей точки процесса.
2	Переходные характеристики необходимо снимать как при положительных, так и отрицательных скачках управляющего сигнала. По виду кривых можно судить о степени асимметрии обьекта. При небольшой асимметрии расчет настроек регулятора рекомендуется вести по усредненным значениям параметров передаточных функций. Линейная асимметрия наиболее часто проявляется в тепловых обьектах управления.
3	При наличии зашумленного выхода желательно снимать несколько переходных характеристик (кривых разгона) с их последующим наложением друг на друга и получением усредненной кривой.
4	При снятии переходной характеристики необходимо выбирать наиболее стабильные режимы процесса, например, ночные смены, когда действие внешних случайных возмущений маловероятно.
5	При снятии переходной характеристики амплитуда пробного входного сигнала должна быть, с одной стороны, достаточно большой, чтобы четко выделялась переходная характеристика на фоне шумов, а, с другой стороны, она должна быть достаточно малой, чтобы не нарушать нормального хода технологического процесса.

Примечание к таблице 20.1: Начальные условия снятия переходной характеристики:
В начальный момент необходимо, чтобы система управления находилась в покое, т.е. регулируемая величина X (например, температура в печи) и управляющее воздействие регулятора Y (выход регулятора на исполнительный механизм) не изменялись, а внешние возмущения отсутствовали. Например, температура в печи оставалась постоянной и исполнительный механизм не изменяет своего положения. Затем на вход исполнительного механизма подается ступенчатое воздействие, например, включается нагреватель. В результате состояние объекта начинает изменяться.

Определение динамических характеристик объекта управления с самовыравниванием по его переходной характеристике. Наиболее часто при определении динамических свойств объекта регулирования применяют ступенчатое возмущающее воздействие, т.е. экспериментально находят переходную функцию объекта (рисунок .20.1). Самовыравниванием процесса регулирования называется свойство регулируемого объекта после нарушения равновесия между притоком и расходом вернуться к этому состоянию самостоятельно, без участия человека или регулятора. Самовыравнивание способствует более быстрой стабилизации регулируемой величины и, следовательно, облегчает работу регулятора. Рассматривается объект с одним входом и одним выходом со свойствами: стационарности, линейности, сосредоточенности параметров. На вход подается ступенчатое воздействие и на выходе снимается кривая разгона. Необходимо решить обратную задачу: по известной кривой разгона определить коэффициенты уравнения.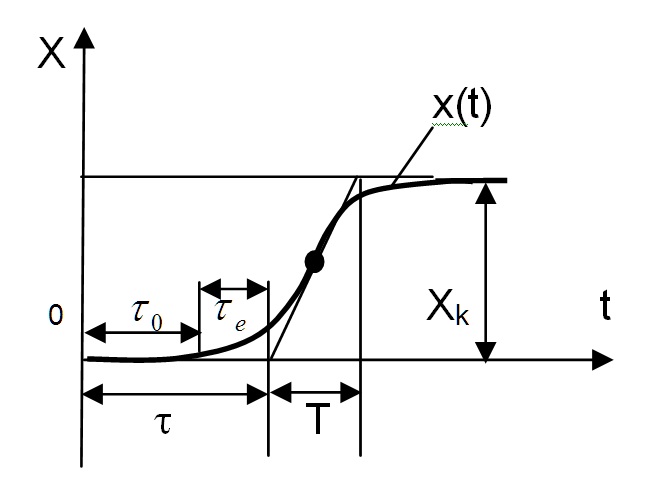



Рисунок .20.1 - . Единичная скачкообразная функция
В то случае, если нас устраивает вид уравнения (*), то его параметры находятся достаточно просто:

• 
  коэффициент усиления - по формуле , где - установившееся значение выхода а – возмущение на входе объекта;
  
• 
  постоянную времени Т – как проекцию касательной к кривому разгону в точке перегиба (см. рисунок .8.6);
  
• 
  время запаздывания - как расстояния от точки 0 до пересечения касательной к кривой разгона в точке перегиба с осью времени (см. рисунок .8.6).
  

Проверка адекватности. Для решения этой проблемы надо выполнить моделирование функции выхода при передаточной функции объекта вида (*). Т.е. рассматривается объект с одним входом и одним выходом со свойствами: стационарности, линейности, сосредоточенности параметров. На вход подается ступенчатое воздействие и на выходе снимается кривая разгона. Необходимо решить прямую задачу по известной передаточной функции определить график кривой разгона. В данном простом примере достаточно воспользоваться уравнением:
(при )

(при )

См. пример на следующей странице на рисунке 20.2, решенный с системе Mathcad. Если значение , найденное по следующей формуле, не превышает 3-7%, то модель считается адекватной: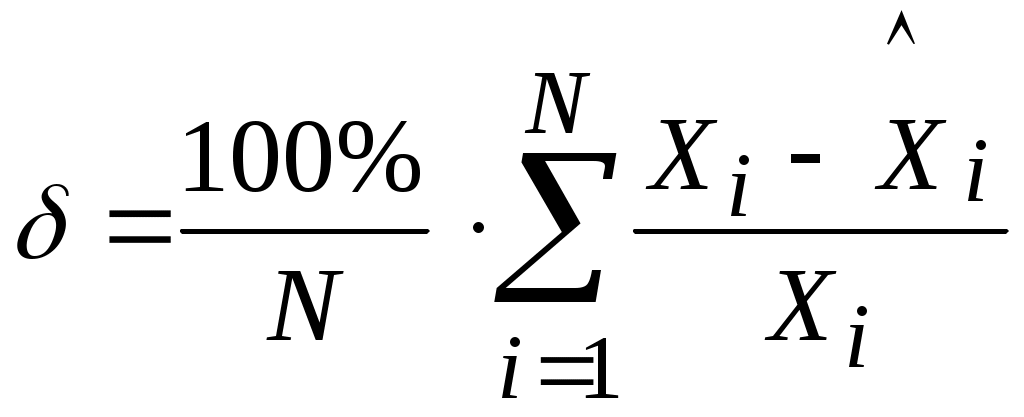



Если окажется, значение ошибки слишком велико, то надо изменить положение касательной на графике (не обязательно, чтобы она проходила через линию перегиба). Если и это не помогает, то надо применить более точный метод получения передаточной функции, например, метод площадей (метод Симою).

Идентификация динамических характеристик объектов с самовыравниванием методом площадей [2-6]. Этот метод является одним из инженерных методов идентификации динамических характеристик объектов управления. Этот метод удобен как для реализации на ЭВМ, так и для ручного счета и обладает вполне удовлетворительной для практики точностью.

Метод предполагает идентификацию вне процесса управления, так как использует не результаты измерений при нормальной эксплуатации САУ, а требуется проведения специальных экспериментов по снятию кривой отклика объекта на ступенчатое возмущение на входе объекта. По этой экспериментально полученной кривой разгона определяется коэффициенты передаточной функции вида: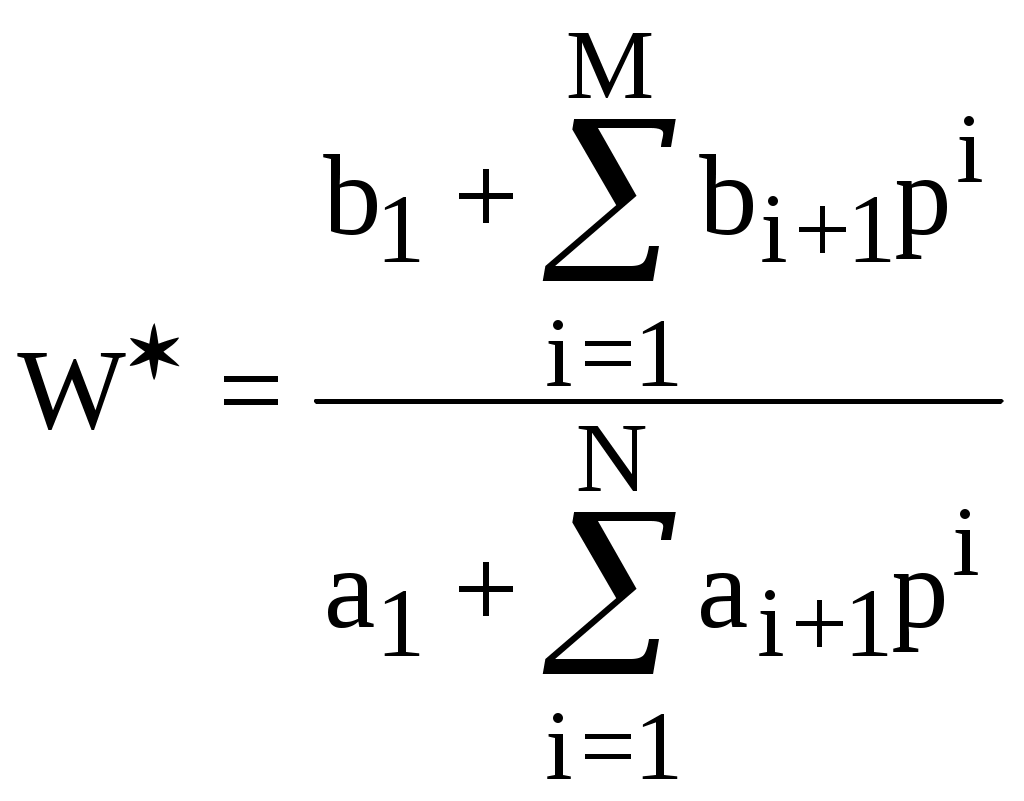

(20.10)

где:

(20.11)
Коэффициент усиления объекта с самовыравниванием рассчитывается по формуле:

(20.12)

Метод применим и для объекта без самовыравнивания.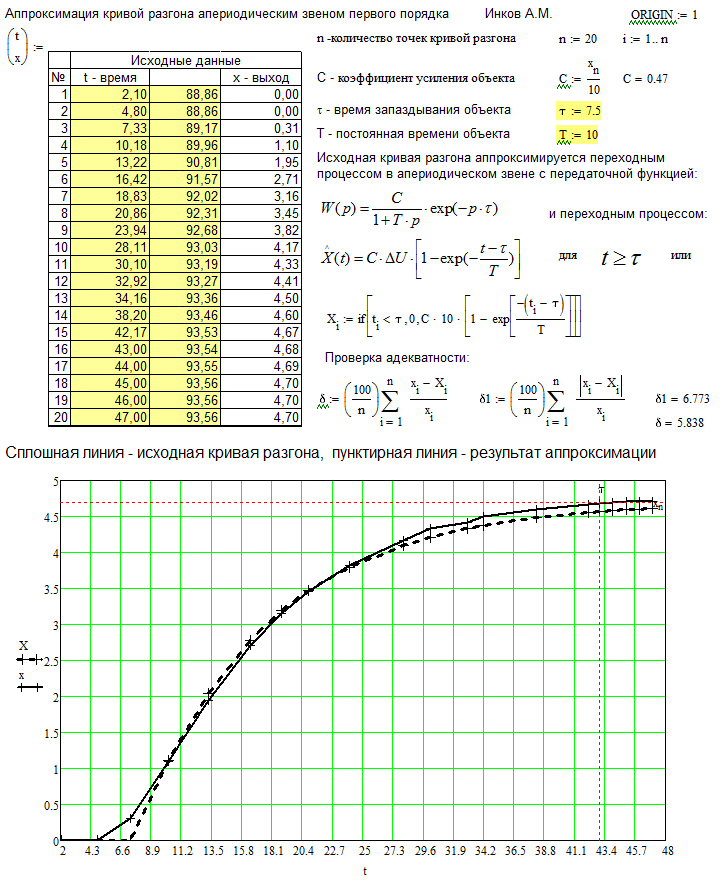


Рисунок .20.2 – Пример проверки адекватности
Время чистого запаздывания определяется из графика кривой разгона как время, прошедшее с момента нанесения возмущения до появления реакции на выходе объекта.

Метод площадей позволяет определить коэффициенты ai, bi, M, N, входящие в (20.11).

Рассмотрим применение метода площадей для определения математической модели стационарного линейного объекта с одним входом и одним выходом, имеющего структурную схему вида: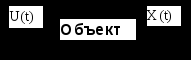



На рисунке 8.8 показана полученная в результате эксперимента кривая разгона. Для обработки используется часть кривой разгона начина с момента времени t= , представленная дискретными значениями выхода X_i, задаваемыми с шагом по времени . Точка t= _принимается за новое начало координат.

При расчетах используется кривая разгона в нормированном виде , которая получается из исходной по формуле :

Z_i = 1-X_i/X_k (20.13)
Суть метода площадей сводится к разложению функции (W*)^-1 в усеченный ряд по степеням p, то есть к разложению:
(20.14)

Интегральные площади F_i, входящие в(5) вычисляются по формулам:

	(20.15)
	(20.16)
	(20.17)

Величины F_i определяются методами численного интегрирования. Например, если воспользоваться методом трапеций, то:

F₁ 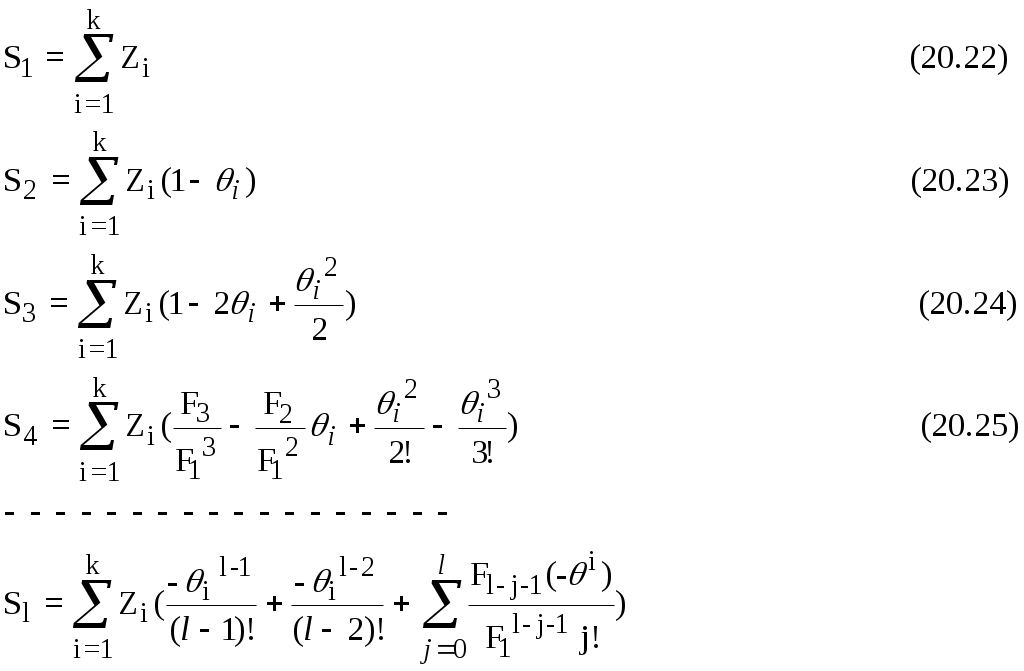= (S₁-0.5) (20.18)

F₂ = F₁ (S₂-0.5) (20.19)

F₃ = F₁² (S₃-0.5) (20.20)

.................

F_l = F₁^l-1 (S_l-0.5) (20.21)
(20.26)

=t_i/F₁ (20.27)
Таким образом, имеем значения Z₁,Z₂,Z_k,нетрудно рассчитать F_i.

Порядок передаточной функции N можно определить из условия, что если F_i мало по сравнению с F_i-1, или если F_i < 0, то N=i-1.

Величина М определяется из условий :

Если X(0)=0, a X’(0)#0, то M=N-1

Если X(0)=X’(0)=0, то M<=N-2

Если X(0)=X’(0)=X’’(0), то b2=b3=b4=...=0

Значения коэффициентов bi и ai находятся решением системы уравнений:

a₁=1; b₁=1

a₂=F₁+b₂

a₃=F₂+b₃+b₂F₁

a₄=F₃+b₄+b₃F₁+b₂F₂ (20.28)

................

a_l=F_l-1+b_l+

В этой системе необходимо подставить нули вместо каждого ai или bi при j>N+1 и j>M+1,а затем решить относительно ai и bi.

При ручном счете обычно ограничиваются вычислением F1,F2,F3 и принимают, что если F3<0, или если X’(0)#0, то М=1, N=2 , то есть передаточная функция W*(p) имеет вид :
…. (20.29)
где:

b₁=1; b₂=-F₃/F₂; a₁=1

a₂=F₁+b₂; a₃=F₂+b₂F (21)

а если X’(0)=0 и F₃>0, то М=0 ,N=3 , а передаточная функция имеет вид :

(20.30)
где :

b₁=1; a₁=1; a₂=F₁; a₃=F₂; a₄=F₃ (20.31)


Рисунок. 20.3А - Возмущение на входе объекта


Рисунок 20.3б - Кривая разгона объекта с самовыравниванием



Рисунок 20.3в - Кривая разгона объекта без самовыравнивания

При ручном счете удобно заносить результаты в таблицу вида:

Таблица 20.2.

ti	Xi	Zi		1-	Zi(1- )	1-2 + 2/2	Zi(1-2 + 2/2)
1	2	3	4	5	6	7	8

Эта таблица содержит К строк. Первые два столбца содержат исходные данные - точки времени и значения выхода. Сумма чисел столбца 4 даст значения S₁, сумма столбца 6- S₂, сумма столбца 8 - S₃.

См. также примеры, приведенные в лабораторной работе №5 [3], где рассмотрены и объекты без самовыравнивания.

Идентификация динамического объекта управления по импульсной характеристике. Иногда по технологическим условиям нельзя длительное время держать «единичный скачок» на входе объекта. Тогда подается возмущение типа «единичного импульса», длительность которого достаточна для заметного изменения выходного сигнала. Практически «единичный импульс» рассматривается как два последовательных «единичных скачка», только первый имеет значение (+1), а второй – (-1). Полученная на объекте экспериментальная импульсная характеристика – график изменения во времени выходного сигнала объекта путем несложных графических преобразований достраивается до экспериментальной кривой разгона и далее поиск математической модели – 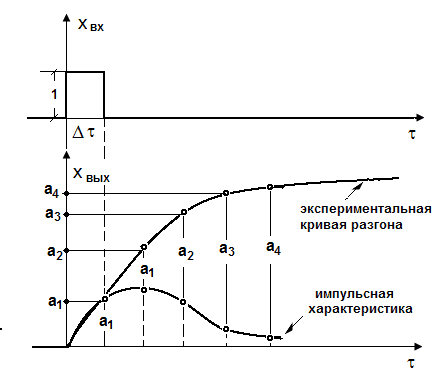идет по указанному выше пути. Перестройка импульсной характеристики объекта до экспериментальной кривой разгона идет так:



Рисунок 20.4 - Схема преобразования экспериментальной импульсной характеристики в кривую разгона.

Основная литература

1. 
   Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с.
   
2. 
   Исмаилов С.У. Современные методы идентификации объектов и систем управления. Методические указания к выполнению лабораторных работ для магистрантов спец. 6М0702. Шымкент, ЮКГУ, 2010 г., -78 с.
   

Дополнительная литература

3. 
   Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с.
   
4. 
   Гроп Д. Методы идентификации систем. - М.: Мир, 1979