Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление

• Название: Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
• Дата: 24.01.2023
• Размер: 4.07 Mb.
• Имя файла: Лекц комплекс СМИОСУ 2017.doc
• Тип: Конспект лекций; #902228
• страница: 13 из 29

Тема3 Моделирование и идентификация динамических характеристик объектов

Лекция 16 Множество моделей, структуры моделей (часть 1)

Математические модели линейных динамических (ММД) объектов и систем и связь между ними. ММД.

Широко используются при анализе и синтезе различных систем автоматизации (см. рисунок 16.1). ММД описывают изменение параметров во времени, в их выражения обязательно прсутствуют производные по времени или другие эквивалентные им параметры. Очень часто (в обоснованных случаях) используют линейные ММД.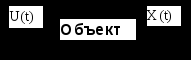



Рисунок 16.1 – Объект динамики
Принято обозначать векторы входных воздействий буквой U (управления), векторы выходных воздействий буквой X (состояния) или Y (выходы), векторы возмущающих воздействий буквой V (на рисунке 16.1 – не показаны)

Все ММД можно разделить на классы.

1 Модели для описания непрерывных систем

Линейные дифференциальные уравнения (ДУ) это наиболее общая форма описания динамики, однако их практическое использование и инженерной практике часто бывает сложным.

Наиболее общий вид записи ДУ:

(16.3).

Передаточные функции (ПФ). В инженерной практике часто используются ММД в виде ПФ. Для объектов с самовыравниванием ПФ в общем виде: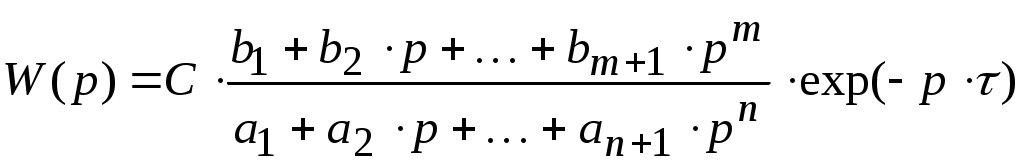

. (n≥m) (16.4)

При использовании «метода площадей» (b1=a1=1) [ ]:

, или (16.5)

(16.6)
Другие виды, например: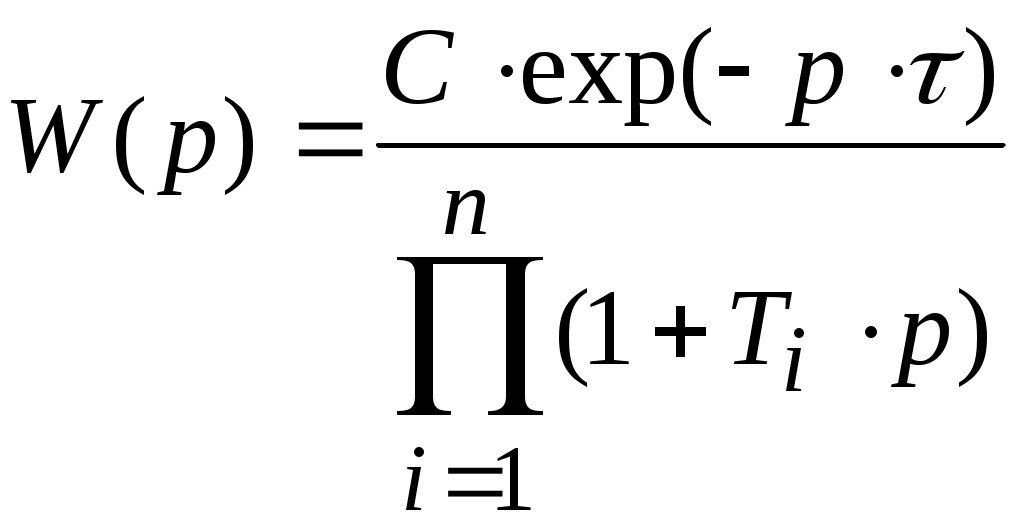

и т.п. (16.7)

Очень часто применяют упрощенное выражение ПФ в виде апериодического звена с запаздыванием:

(16.8)

Для объектов без самовыравнивания используется передаточная функция в общем случае используется в виде: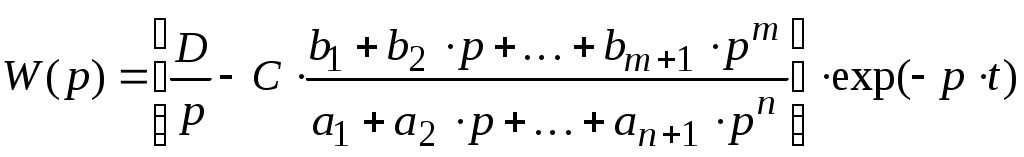

(16.9)

(обращаем внимание на то, что здесь присутствует интегральная составляющая - величина 1/р)

или упрощенные выражения для объектов без самовыравнивания:

или: (16.10)

(16.11)
Конкретный вид W(p) выбирается из условия обеспечения адекватности и удобства вычислений.

Адекватность математической модели может быть, например, оценена по формуле (16.12). Если значение , найденное по этой формуле, не превышает 3-7%, то модель считается адекватной: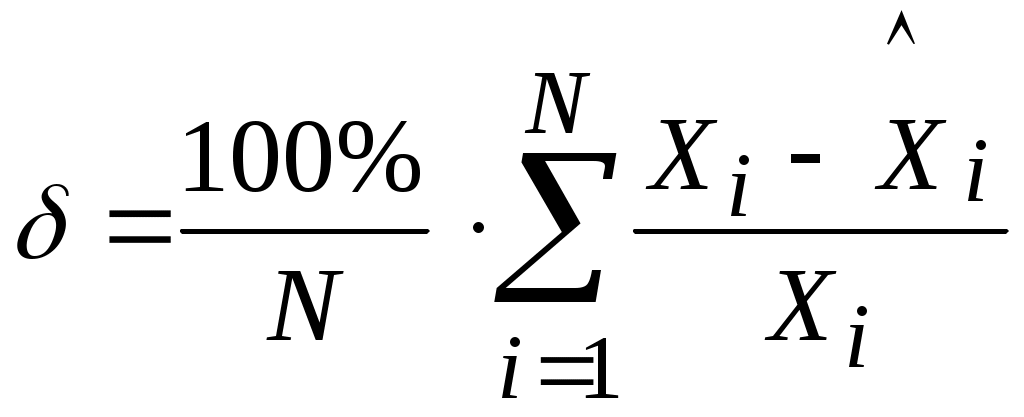

(16.12)

Для уравнения вида (16.8) выход определяется аналитически по формуле:

(при ) (16.13)

(при ) (16.13A)
а для W(p) вида (16.7) при n=2:



(16.14)
В более общем случае в качестве критерия соответствия при решении данной задачи берут критерий вида:

min(F_ai), (16.15)

где – экспериментальное значение;

– расчётное значение.

Для нахождения коэффициентов a_i составляют уравнения:

(16.16)

Таким образом, получается система уравнений, решая которую можно определить a_i.

Частотные характеристики (ЧХ). При подаче на вход линейной системы сигнала:

(16.17)
на выходе будет сигнал:

, (16.18)

а АФЧХ имеет вид: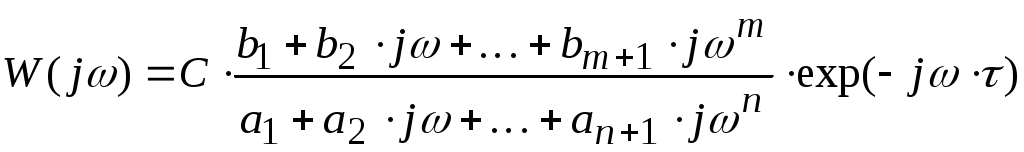

=

(16.19),
Где:

(16.20)

(16.21)
Используются также весовые функции:

, (16.22)

И системы матричных линейных уравнений пространства состояния:

Модель в пространстве параметров состояния

, (16.23)

где

U - вектор входа; x - вектор переменных состояния; y - вектор выхода системы;

А - матрица динамики системы; В - матрица управления; С^T - матрица измерения (датчиков)
или
, (16.24)
Модели для описания дискретных систем

Линейные разностные уравнения

Математические модели в цифровых системах управления записываются в виде рекуррентных разностных уравнений.

Если математическая модель ТОУ представлена передаточной функцией вида (16.8) и использован фиксатор нулевого порядка, то выход объекта в цифровом виде для момента времени определяется как:

(16.25)

где , ,

Уравнение (16.25) является разностным эквивалентом непрерывного уравнения объекта (16.8) для дискретных моментов времени j = 1, 2, 3, ….

D - число, округленное до ближайшего большего целого, определяет запаздывание ТОУ, выраженное в целом числе периодов опроса .

Для j < D:

- выход объекта в момент времени - , т.е. на прошлом шаге опроса.

- управляющее воздействие (выход регулятора) в момент времени -D.
Дискретные передаточные функции: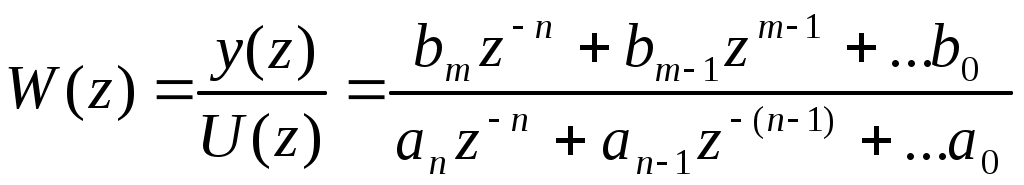

(16.26)
Модель в пространстве параметров состояния
x(k+1)=A*x(k)+B*U(k) (16.27)

y(k)=Cт*x(k)
Цифровые разностные рекуррентные уравнения:

. (16.29)

Модели для описания нелинейных систем (см рисунок 16.2)
u(t)=δ(t) y(t)=ω(t)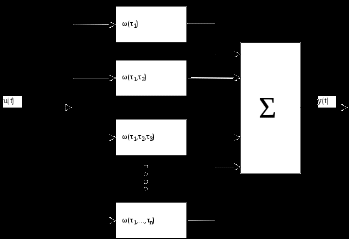



(16.30)

(16.31)


Рисунок 16.2 – нелинейные модели динамики
Стохастические модели. Модель нелинейной системы с использованием ядер Вольтера. При рассмотрении явлений в моделях с шумами принято оценивать влияние шумов на процесс идентификации путем использования понятий авто - и взаимно - корреляционной функций. Оценку влияния шумов можно производить, если процесс описания шумов описать следующим уравнением:

(16.31)

R_uu- автокорреляционная функция входного сигнала (см. в лекции 6);

R_uy- взаимнокорреляционная функция входного и выходного сигнала.

Если u(t) – это случайный стационарный процесс и y(t) тоже, то, применяя эти понятия не учитывают, что R_uu и R_uy позволяют оценить величину случайной составляющей, то, решая это интегральное уравнение мы можем получать оценки с учетом помех входа и выхода. Задача имеет решение при условии, что входной сигнал можно измерять “абсолютно” точно, а выходной сигнал содержит все аддитивные составляющие помехи.

Таким образом по типу идентифицируемой модели можно выделить: линейная и нелинейная; детерминированная и стохастическая; с непрерывным и дискретным временем; стационарная и нестационарная; одномерная и многомерная; статическая и динамическая; с сосредоточенными и распределёнными параметрами. Магистрант должен уметь привести примеры таких объектов.

Свойства идентификации: управляемость, наблюдаемость, идентифицируемость.

Управляемость – система управляема, если для любого момента времени при любых состояниях существует такое управление u, которое переводит начальное состояние системы в конечное.



где n – порядок системы; А – матрица коэффициентов при х;

В – матрица коэффициентов при r.

Условием управляемости системы является то, чтобы не был равен нулю.

Наблюдаемость – система наблюдаема, если любое или все ее состояния можно непосредственно или косвенно определить по выходному вектору системы.

, где С – матрица выхода, коэффициенты при у.

Хотя бы один минор не должен быть равен нулю, в этом случае система наблюдаема.

Идентифицируемость – система идентифицируема, если по изменениям координат состояния системы можно определить ее параметры.

,

где V(0) – вектор начальных условий; Ап – матрица перехода.

,

где АR – расширенная матрица; I – единичная матрица.

Система идентифицируема, если .

Идентификация динамических систем. Допустим, динамическая система описана передаточной функцией следующего вида: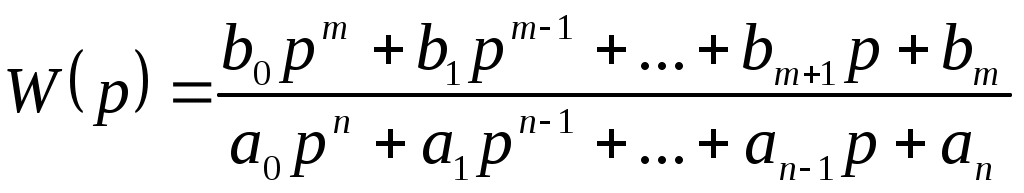



Получаем систему дифференциальных уравнений первого порядка из n - уравнений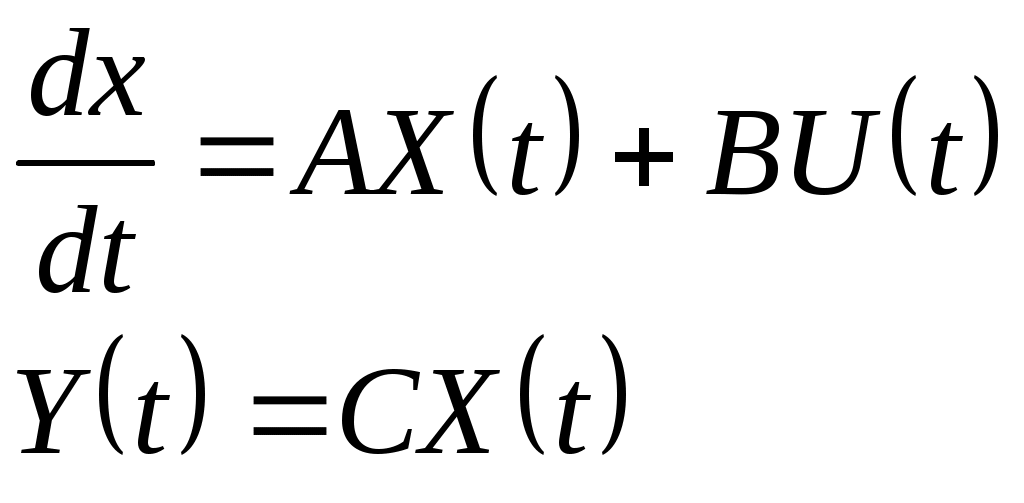



где Y – выходные переменные, U(t) – входные переменные, Х – внутренние переменные.

Как получить эту систему?

I. а) б)

в) Замена переменной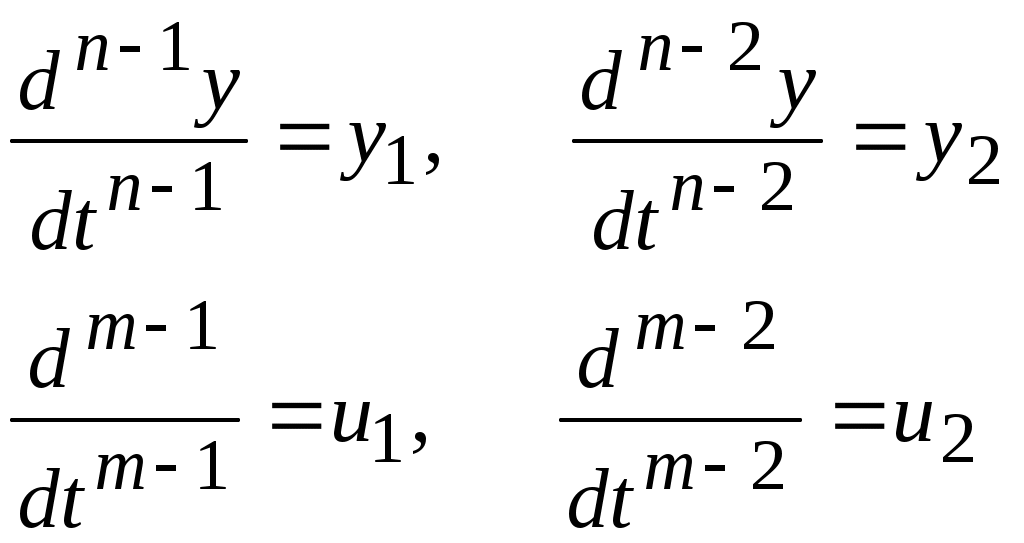

г) получаем систему n – го порядка дифференциальных уравнений первого порядка.

C помощью методов пространства состояния.

2. От дифференциальных уравнений переходим к разностным уравнениям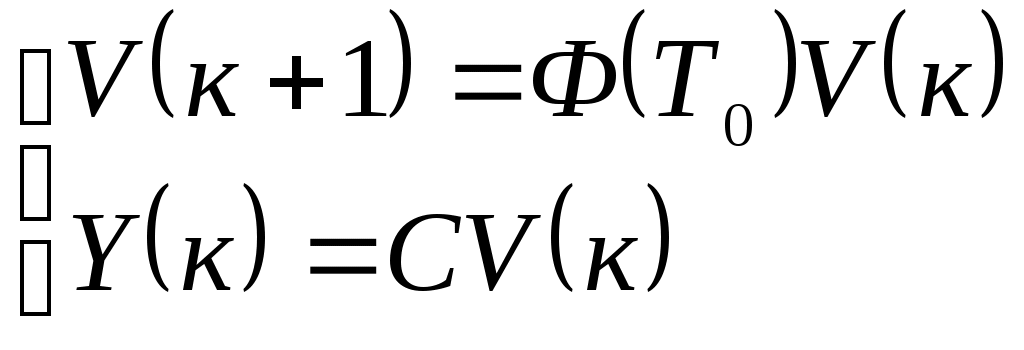



где - обобщенный вектор.

3. получаем матрицу перехода:

,

при этом V(к) при е измерений примет значение: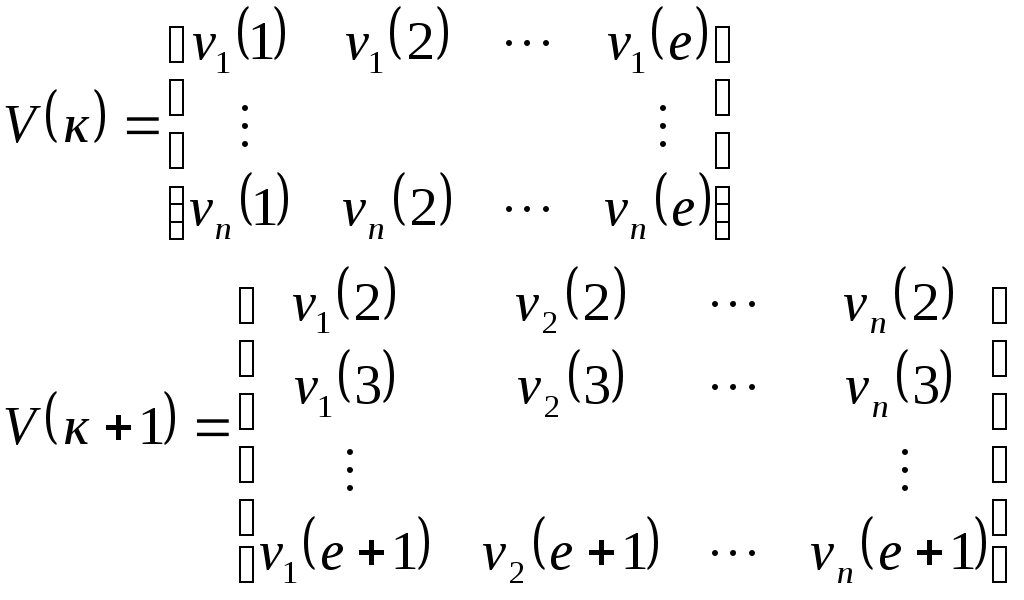



Если 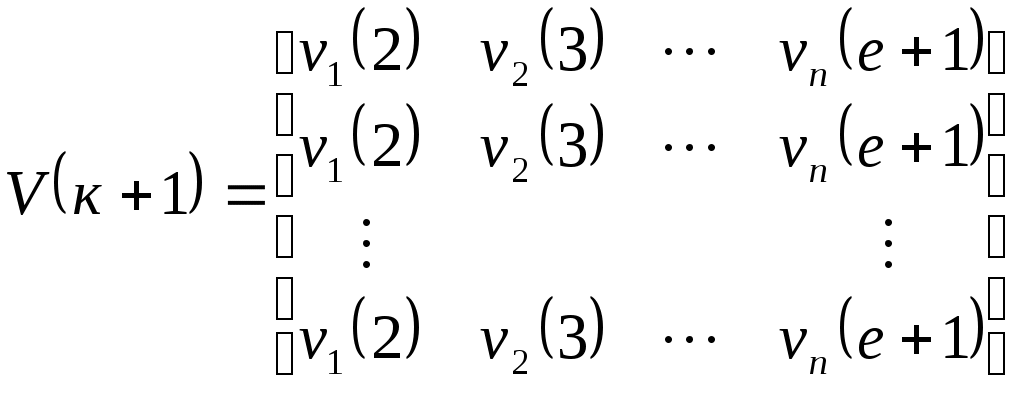, то при



Количество измерений определяется по аналогичной формуле для линейного регрессионного анализа.

Основная литература

1. 
   Построение математических моделей химико-технологических процессов. Под ред. Дудникова Е.Г. - Л.: Химия, 1970. –312 с.
   
2. 
   Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с.
   
3. 
   Гроп Д. Методы идентификации систем. - М.: Мир, 1979
   

Дополнительная литература

4. 
   Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с.